|
Cite this article as: Li Y, Pang Y, Vigneron D, Glenn O, Xu D, Zhang X.
Investigation of multichannel phased array performance for fetal MR imaging
on 1.5 T clinical MR system. Quant Imaging Med Surg 2011;1:24-30. DOI:
10.3978/j.issn.2223-4292.2011.11.04
Original Article
Investigation of multichannel phased array performance for fetal MR
imaging on 1.5T clinical MR system
1Department of Radiology and Biomedical Imaging, University of California San Francisco; 2UCSF/UC Berkeley Joint Graduate Group in Bioengineering, San Francisco, CA, USA
|
|
Abstract
Fetal MRI on 1.5T clinical scanner has been increasingly becoming a powerful imaging tool for studying fetal brain
abnormalities in vivo. Due to limited availability of dedicated fetal phased arrays, commercial torso or cardiac phased arrays
are routinely used for fetal scans, which are unable to provide optimized SNR and parallel imaging performance with a small
number coil elements, and insufficient coverage and filling factor. This poses a demand for the investigation and development
of dedicated and efficient radiofrequency (RF) hardware to improve fetal imaging. In this work, an investigational approach
to simulate the performance of multichannel flexible phased arrays is proposed to find a better solution to fetal MR
imaging. A 32 channel fetal array is presented to increase coil sensitivity, coverage and parallel imaging performance. The
electromagnetic field distribution of each element of the fetal array is numerically simulated by using finite-difference timedomain
(FDTD) method. The array performance, including B1 coverage, parallel reconstructed images and artifact power,
is then theoretically calculated and compared with the torso array. Study results show that the proposed array is capable of
increasing B1 field strength as well as sensitivity homogeneity in the entire area of uterus. This would ensure high quality
imaging regardless of the location of the fetus in the uterus. In addition, the paralleling imaging performance of the proposed
fetal array is validated by using artifact power comparison with torso array. These results demonstrate the feasibility of the 32
channel flexible array for fetal MR imaging at 1.5T.
Key words
Fetal array; multichannel phased array; finite-difference time-domain; parallel imaging; MRIQuant Imaging Med Surg 2011;1:24-30. DOI: 10.3978/j.issn.2223-4292.2011.11.04
|
|
Introduction
Fetal magnetic resonance imaging (MRI) on 1.5T clinical scanners
has increasingly been performed to detect the brain abnormalities and
potential neurodevelopmental disabilities since its first introduction
in early 1980s (1-9). Due to fetal motion, multiecho ultrafast MRI
techniques such as single-shot fast spin-echo (ssFSE) and half-Fourier
acquired ssFSE are primarily used but at the price of signal-to-noise ratio (SNR) degradation. Parallel acquisition (10-12) and excitation, as
a fast imaging technique, are feasible for fetal MRI with less focal SAR
hot spots, higher SNR and reductions in scan time (13,14). However,
since there are no dedicated fetal phased arrays available, commercial
torso or cardiac phased arrays are routinely used instead, which are not
optimized in SNR, safety and parallel imaging performance for fetal
MRI, due to the limited coil elements, filling factor and B1 field coverage.
This poses a demand for investigation and development of dedicated
radiofrequency (RF) hardware for efficient MR signal excitation and
reception in fetal imaging.
Previous work demonstrates that well designed flexible transceiver
arrays using microstrip elements (15-21) are feasible for various subjects
with different sizes (22,23), which suggests the possibility of utilizing
flexible phased array in fetal MRI. Current research has shown the
significant SNR improvement in the region near the coil array as well as
the deep region of a maternal body model by increasing the number of
coil elements (24,25). By optimizing coil configuration and increasing
coil elements, the filling factor and imaging coverage can be improved
to achieve high SNR, therefore, higher spatial resolution, sensitivity, and image homogeneity, and reduce scanning time in clinical fetal MRI.
Numerical calculation of RF electromagnetic fields in human
models with realistic geometry and tissue properties using finitedifference
time-domain (FDTD) algorithm is an efficient means in
evaluating and optimizing coil configuration for better transmit/receive
performance in MR imaging (26,27). The numerical calculation results
lead to prospective insight into the coil performance for fetal MRI such
as SNR, specific absorption rate (SAR) and parallel imaging feasibility,
which provides important guideline for fetal array design and fabricating
prototype coil arrays (28-32).
In this work, we propose a flexible 32-channel fetal phased array
design to increase SNR, imaging coverage, parallel imaging performance
and imaging safety in the whole uterus region. The performance of the
proposed flexible array is investigated numerically and compared with
the commercial 8-channel torso array at 1.5T. The B1 field distribution
of the proposed fetal array is analyzed by using FDTD method. In
addition, GRAPPA reconstructed images with different acceleration
factors are generated based on simulation results. Artifact power is
measured to quantitatively evaluate parallel imaging performance.
|
|
Materials and methods
In order to improve imaging coverage and filling factor, the element
number of dedicated fetal array increased to 32 while the size of each
element was reduced correspondingly to cover the abdomen of mother.
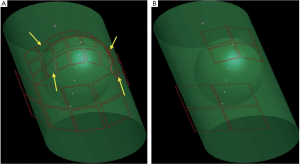
As shown in Figure 1, the fetal array consisted of 4×2 square surface
coils with 110 mm width and 160 mm length on the bottom and 8×3
coils with 60 mm width and 70 mm length at the top except the four
trapezoidal coil indicated by yellow arrows. By increasing the number
of coil elements and the relative small size of each element, the array
is more flexible, suitable for patients with different abdomen sizes and
shapes. Compared with the 8-channel commercial torso array, which
consisted of 4 square surface coils with 160 mm width and 160 mm
length on the bottom and the other four with 110 mm width and 110
mm length at the top as shown in Figure 1, the coverage and filling
factor were improved along with the increased flexibility.
The simulations of the two arrays were carried out using commercial
FDTD software XFDTD 6.5 (REMCOM Inc., State College, PA) to
compare array performance. The conductors (red region) were copper
tapes (σ=5.8×107 S/m, μr=1 and 3 mm in width). The phantom (green
region, σ=0.7 S/m and μr=72) was ellipse cylinder with 800 mm length,
205 mm long axel and 120 mm short axel, combined with a sphere with
140 mm radius. In order to achieve better coverage and filling factor,
the coil elements at the top of the torso array were rotated 15º along
the anterior-posterior direction. All the elements of the proposed fetal
array were placed close to the phantom. A three-dimension FDTD
simulation was performed at 64 MHz, corresponding to the proton
Larmor frequency at 1.5T. Each element of the two arrays was excited by sinusoidal current source with RMS value of 1A and the same phase.
Outer boundaries were absorbing perfectly matched layer (PML) with 7
layers. The meshing cells of the two models were 3 mm × 3 mm × 5 mm.
To evaluate the parallel imaging performance of the fetal array, GRAPPA
(12,33-35) algorithm was utilized for image reconstruction. The
electromagnetic field distribution of each element coil was simulated
separately. The images of each element were calculated pixel by pixel
based on simulation results. Ignoring relaxation and susceptibility
effects, the gradient echo image intensity SI is given by (36,37).
 where C is constant proportional to resonance frequency and initial
magnetization, γ is the magnetogyric ratio, τ is the RF pulse duration,
B1+ and B1- denote the positive and negative circularly polarized
component respectively and the asterisk denotes a complex conjugate
operation (38,39). As the phantom is assumed to be uniformly excited,
SI is proportional to | B1-*| according to equation [1]. A second order
polynomial fit is performed to smooth the images.
The GRAPPA reconstruction was carried out by using PULSAR
toolbox (40). 32 Auto-Calibration Signal (ACS) lines in the center
of the k-space were used to estimate the missing lines. The block size
was 2. All the coils were used for GRAPPA reconstruction. The coil
distribution was set to linear. 90% of k-space along frequency-encoding
direction was employed for fitting. The GRAPPA reconstruction with
subsampling factors of 2, 4, 6 and 8, corresponding to acceleration
factors of 1.7, 2.6, 3.2 and 3.5 respectively, was performed to A/P
direction in axial plane. Sum-of-square (SoS) images were calculated as
reference (41).
Figure 1. Configurations of coils and phantoms, 32 channel fetal array (A) and 8 channel torso array (B).
|
|
Results
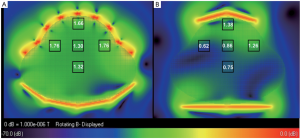
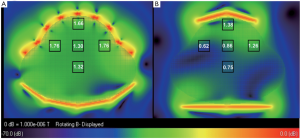
The B1 field distributions in the transversal and sagittal planes of the
two arrays, which was scaled to 2×10-7 W input power of each element,
was shown in Figure 2 and Figure 3. The mean B1 in 3 cm × 3 cm region
at different location in the whole uterus was shown in the black boxes.
As shown in Figure 2, B1 was increased 20% in the surface region at the
center of transversal plane, whilst that on left and right sides increased
40% to 180% due to the better coverage of the 32 channel fetal array. As
shown in Figure 3, B1 increased 50% in the center of surface region as
well as that on the anterior and posterior sides was increased 28% due
to better filling factor of the fetal array. B1 in the center of uterus and in
deeper region such as the center of the patient was increased 87% and
79% respectively because of increasing the number of element. Besides
the improvement of B1 field strength, the sensitivity homogeneity also
increased substantially which is important for fetal MRI due to the
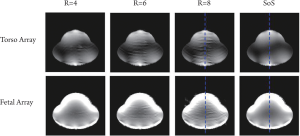
possibility of fetus head location in the whole uterus.
The GRAPPA and sum-of-square reconstructed images were shown in Figure 4. The first row was the images of eight-channel torso array
and the second row was of 32-channel fetal array. Artifact power was
calculated to quantitatively evaluate the parallel imaging performance of
two arrays. The artifact power (AP) was defined as (40).
 where ISoS and IGRAAPA were the image intensity of sum-of-square
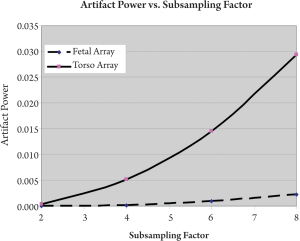
images and GRAPPA reconstructed images. As shown in Figure 5, the
fetal array dramatically reduced the artifact power compared with the
torso array. The artifact power of fetal array with subsampling factor 8
was diminished to 7.8% of that of torso array. Figure 6 showed the image
intensity of SoS and GRAPPA reconstructed images with subsampling
factor 8 at the center line, which demonstrated the image intensity of
the fetal array increased 5-fold in surface region. The zoom-in image in
Figure 6 showed 50% improvement in the deeper region compared with
that of torso array, although the sizes of each element of the fetal array
were smaller than torso array (42).
Figure 2. B1 map of (A) 32 channel fetal array and (B) 8 channel torso array in the central transversal plane of the phantom calculated by XFDTD. The numbers in the boxes indicated the mean B1 (10-8T) in the 3 cm × 3 cm region.
Figure 3. B1 map of (A) 32 channel fetal array and (B) 8 channel torso array in the central sagittal plane of the phantom calculated by XFDTD. The numbers in the boxes indicated the mean B1 (10-8T) in the 3 cm × 3 cm region.
Figure 4. GRAPPA reconstructed images. 32 Auto-Calibration Signal (ACS) lines in the center of the k-space were used to estimate the missing lines. The GRAPPA reconstruction with acceleration factors of 1.7, 2.6, 3.2 and 3.5 was performed to A/P direction in axial plane.
Figure 5. Artifact power comparison between fetal array and torso array with subsampling factors of 2, 4, 6, and 8.
Figure 6. The image intensity of SoS and GRAPPA reconstructed images with subsampling factor 8 at the center lines (blue dash lines in Figure 4). The right figure is zoom-in image, showing image intensity in deeper region in uterus.
|
|
Conclusions and Discussions
This study indicates the proposed 32-channel fetal array improves
SNR, sensitivity homogeneity and imaging coverage by increasing the
number of array element. The artifact of parallel reconstructed images
is reduced dramatically by using the proposed flexible fetal array. These
results demonstrate the feasibility of the 32 channel flexible array and the
performance improvement over the torso or cardiac array, providing a more
sensitive, faster and safer imaging method for fetal MR imaging at 1.5T.
Some B1 drop-off near the surface of maternal body model as shown
in Figure 2 and Figure 3 can be observed. This field distribution can be
further improved by performing B1 shimming with the fetal array or fine
adjusting the phase and amplitude on the array elements, or even by
simple post-processing during the image reconstruction. This certainly
deserves a further study.
With the use of multichannel RF transmitter, the flexible fetal array can
be also used as a transmit/receive array to perform regularly transmitting
or parallel excitation for B1 filed shimming and fast selective excitation.
Since the region of interest is relatively smaller than the maternal
abdomen, the excitation power can be reduced by using transmit array
instead of regular body coil. Therefore, the average SAR and resulting
temperature rise will decrease which improves patient safety.
|
|
Acknowledgment
This work was supported in part by NIH grants EB004453, EB008699, EB007588-03S1 and P41EB013598, and a QB3 Research Award, and UCSF Radiology seed grant (10-41).
|
|
Disclosure
Authors have no conflict of interest to disclose.
|
|
References
|
