Quantitative X-ray fluorescence imaging of gold nanoparticles using joint L1 and total variation regularized reconstruction

Introduction

Nanoparticles have been intensively investigated in medicine as molecular contrast agents for targeted imaging and as drug carrier for targeted therapy (1). They can passively leak into the tumor interstitium through the “Enhanced Permeability and Retention (EPR)” phenomenon (2). The tumor-targeting specificity can be improved by conjugating nanoparticles with tumor-specific antibodies, ligands, or receptors (3). Among many types, gold nanoparticles (GNPs) exhibit particular potential for clinical application, because of their chemical inertness, molecular stableness, and facile surface modification (4). Furthermore, GNP presents unique physical responses to X-ray and near-infrared light, inducing secondary radiation for enhanced radiotherapy and heat for photothermal therapy (5-8).

Specific and quantitative GNP imaging is crucial for cancer diagnosis and treatment assessment in the situation where GNP severs as targeting probes. The X-ray absorption coefficient µ depends strongly on the atomic number of the absorbing material. The high atomic number of Au enables high absorption, making GNP an effective X-ray contrast agent. Micro-computed tomography (micro-CT) has been used to quantify GNP within murine tumors (9-11). However, X-ray absorption in transmission CT is a combined effect of material type and its concentration/density. Multiple materials of different concentrations might result in the same absorption, which means that conventional CT is not able to decompose the material type and its concentration/density. In contrast, X-ray fluorescence tomography (XFT) provides distinct advantages over CT in quantification of GNP and other high-Z probes (12,13). Its high specificity and quantitative feature is achieved by detecting the characteristic X-ray fluorescence (XRF) emanating from excited high-Z probes. It has been demonstrated that XFT as a molecular imaging technique can recover the in vivo biodistribution of high-Z probes (14,15). Moreover, XFT possessed unique potential in simultaneous imaging of multiple high-Z molecular probes (13), and thus to monitor different molecular activities at the same time.

The development of benchtop XFT systems, using ordinary polychromatic X-ray sources instead of synchrotron sources, accelerates the application of XFT in molecular imaging field (16,17). GNP can be imaged with either K-shell (67.0 and 68.8 keV) or L-shell (9.7 and 11.6 keV) XRF. K-shell XFT enables imaging at larger depth in tissue. L-shell XFT can be used to image shallow tumors, but with higher detection sensitivity, due to increased photoelectric cross-section, reduced Compton scattering, and better detector energy resolution at lower energy (18-20). L-shell XFT has been verified by Monte Carlo simulation for its higher sensitivity (3.0–4.4 times better than K-shell imaging) in imaging small objects (21).

XFT is commonly reconstructed using filtered back projection (FBP) or maximum likelihood expectation maximization (ML-EM) methods (17,18). Due to high attenuation of L-shell XRF, attenuation correction is crucial for quantitative L-shell XFT imaging (21). Moreover, because of the limited XRF counts, L-shell XFT reconstruction is susceptible to noise and thus necessitates regularization. GNPs used in XFT are designed to specifically target the tumor. Consequently, the reconstructed image tends to be sparse with localized high concentration in the tumor region. Therefore, we introduced joint L1 and total variation (TV) regularization to enforce the sparsity and promote the smoothness while preserving target edges (22,23). We employed a nonlinear conjugate gradient (NCG) descent algorithm with backtracking line search to solve the L1 + TV regularized reconstruction problem (24).

The goal of this work is to evaluate the joint L1 + TV regularized XFT reconstruction method in quantitative imaging of GNPs. We first built a dual-modality XFT/CT imaging system consisting of an X-ray tube, a 3D-printed pencil beam collimator, a translation/rotation stage, an X-ray flat panel detector and an XRF spectrometer. Then, we conducted experiments by imaging a water phantom embedded with GNP vials of various concentrations. We compared the L1 + TV regularization method with FBP, ML-EM, L1 regularization and TV regularization methods. The performance of different reconstruction methods was quantitatively evaluated using contrast-to-noise ratio (CNR), Dice similarity coefficient (DSC), and localization error (LE) metrics.

Methods

Dual-modality XFT/CT imaging system

The experimental setup of the developed XFT/CT system is shown in Figure 1. An X-ray tube (MXR 225/22, COMET AG, Flmatt, Switzerland) with two selectable focal spots (1.0 and 5.5 mm) was employed. There was an inherent 0.8-mm-thick beryllium filter at the tube exit window. An 8.9-cm-long pencil beam collimator was aligned to the central axis of the X-ray beam. It was 3D printed with stainless steel and has a 0.5 mm pinhole in the nozzle. A 2-mm-thick Al filter was placed at the outlet of the collimator, to suppress the L-shell XRF from the tungsten target of the X-ray source and to minimize overlap with the gold L-shell XRF. The imaged object was positioned on a translation/rotation stage (Thorlabs, Newton, NJ, USA). The source-to-rotation axis distance was 35.0 cm, and the source-to-flat panel detector distance 52.5 cm. The full width at half maximum (FWHM) of the pencil beam was 2 mm at the imaging isocenter, and 3 mm at the imaging panel. A single-pixel silicon drift detector (SDD, Amptek, Bedford, USA) with a 70 mm² active area was placed 10 cm from the isocenter at 120° to the excitation beam. This SDD detector is designed for spectrum detection of low-energy X-rays. It is featured with a 122-eV energy resolution at 5.9 keV and a count rate over 1×10⁶ counts per second. An amorphous silicon flat panel detector (PerkinElmer, Waltham, MA, USA) with a 20×20 cm² active area and 200 µm pixel resolution was used to acquire cone beam transmission X-ray projections for CT imaging.

Figure 1 Dual-modality XFT/CT imaging system. (A) Schematic diagram and (B) photograph of the XFT/CT system. (C) The pencil beam collimator 3D printed using stainless steel. It has a 0.5 mm pinhole at the nozzle. (D) The pencil beam projection on the flat panel detector (FPD). (E) The profile along the diameter of the pencil beam projection in (D). The full width at half maximum (FWHM) of the pencil beam is 3.0 and 2.0 mm, respectively, at the imaging panel and imaging isocenter. XFT, X-ray fluorescence tomography.

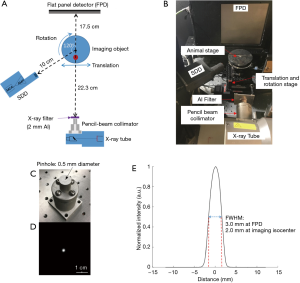
GNP and phantoms

Commercially available GNP of 15 nm diameter (AuroVist, Nanoprobes, Yaphank, NY, USA) was used as the imaging agent. For detection calibration, the original GNP sample of 200 mg/mL was sequentially diluted to various concentrations. GNP solutions of 150 µL and 0.02–2.5 wt.% concentrations were filled into small vials of 6 mm diameter, and positioned at the imaging isocenter for XRF acquisition.

For tomographic imaging, two water phantoms with 2 or 4 GNP vial inserts were customized. The phantoms were 3 cm in diameter and 4.5 cm in height. Two configurations were used to evaluate the XFT reconstruction algorithms: (I) a two-target water phantom with GNP vial inserts of 0.16 and 0.08 wt.%; (II) a four-target water phantom with GNP vial inserts of 0.16, 0.08, 0.04 and 0.02 wt.%.

Data acquisition

The 1 mm focal spot of the X-ray tube was selected for XRF excitation. After optimizing voltage and current, the X-ray tube was set at 64 kVp and 10 mA to maximize XRF production. The SDD was operated at a bias voltage of −133 V with 4 µs peak time and 3× gain. For XFT imaging, the phantom was positioned on the translation/rotation stage and aligned to the imaging isocenter. Then the height of the stage was adjusted to align the imaged slice to the plane of the pencil beam and SDD. In order to fully cover the field of view, there were 21 stage translation steps with a 1.5 mm step size. After each translation, the stage was rotated by 10 degree for full 360° coverage. The XRF acquisition time was set to 30 sec per projection. In total, the data acquisition included 36×21 pencil beam excitations.

After XFT acquisition, the pencil beam collimator was retreated, and CT imaging was conducted. The settings of the X-ray tube were: 1 mm focal spot, 45 kVp voltage and 2.5 mA current. A 0.5-mm-thick Cu filter was used. The stage was rotated every 1° for full 360° coverage. The exposure time of the FPD was 124 ms per projection. CT was reconstructed with the Feldkamp-Davis-Kress FBP reconstruction algorithm (25).

XRF analysis

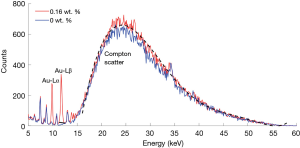
An example of the measured XRF spectrum for solutions with and without GNP is shown in Figure 2, with Au Lα and Lβ XRF peaks clearly distinguished. Other peaks within the 5–13 keV region were originated from the shielding lead (Pb, Z=82) material. The Lβ peak over the 11.2–12.2 keV area was selected for XRF analysis, considering its higher yield and lower attenuation than Lα peak. The net XRF counts P_net in the region of interest (ROI) were extracted after background subtraction. The background counts were linearly interpolated through the selected energy window. To offset the absorption of the excitation X-ray beam and emission XRF, the Compton scatter was used to normalized the XRF signal: P_FS = P_net/P_C, where P_FS is the normalized XRF signal and P_C is the peak value of the Compton scatter. This fluorescence-to-Compton normalization also neutralized the geometrical variations among incident beam, sample and detector (19,26). For scatter calculation, the Compton scatter profile was fitted using the 6^th order polynomial (shown in Figure 2).

Figure 2 A representative XRF spectrum of GNP. The line under Au-Lβ peak denotes the linear interpolation of the background which was subtracted in XRF signal extraction. The dotted line is the 6th order polynomial fit used in Compton scatter estimation. XRF, X-ray fluorescence; GNP, gold nanoparticles.

XFT reconstruction

XFT sinogram, with 21 translation and 36 rotation steps, was created. For each pencil beam excitation, the detected XRF counts are related to the GNP concentration in the object, which can be expressed as:

where p_i is the detected XRF counts when the beam i was exciting the imaging object. c_ij is the probability that a XRF photon is emitted from pixel j excited by the beam i, and calculated as the length of the intersection between the excitation beam i and the pixel j. For L-shell imaging, the attenuation of the excitation beam and XRF must be taken into account. $e^{-{\mu }_e{e}_{ij}}$ denotes the attenuation of the excitation beam, where μ_e (0.075/mm) is the linear attenuation coefficient of water at the mean energy (21 keV) of the excitation X-ray, and e_ij is the distance through water the excitation beam i travels to pixel j. $e^{-{\mu }_f{f}_{ij}}$ denotes the attenuation of the XRF, where μ_f (0.347/mm) is the linear attenuation coefficient of water at Au-Lβ energy, and f_ij is the distance through water the XRF travel from pixel j toward the SDD detector. I₀ is the intensity of the excitation X-ray beam, η is the XRF yield, μ_ph is the photoelectric mass absorption coefficient of Au, and G_j is the Au concentration at pixel j.

The XFT reconstruction problem can be recast into a matrix equation:

where P denotes the vector of measured XRF counts, M is the system matrix representing the physical model of XFT imaging, and X is the vector of reconstructed pixel values which are proportional to the GNP concentration.

The goal of XFT reconstruction is to obtain GNP distribution X from measurement P based on Eq. [2]. However, no direct solution of Eq. [2] exists, due to the ill-condition of the system matrix M . To generate numerically stable solutions, joint L1 and TV regularization was incorporated and the resulting optimization problem is:

where the cost function f(X ) contains data fitting, sparsity penalty and smoothing penalty terms. λ_L1 and λ_TV are the L1 and TV regularization parameters, respectively.

Eq. [3] is solved through the NCG decent algorithm with backtracking line search (24), where the gradient of the cost function is expressed as:

The L1 norm ${\Vert X\Vert }_1$ is the sum of absolute values $\left|X\right|$ . Owing to the non-smoothness of absolute function, the derivative of‖X‖1 does not exist everywhere. For gradient calculation in Eq. [4], sparsity penalty ${\Vert X\Vert }_1$ is approximated as a smooth function using $\left|X\right|\approx \sqrt{X^{T}X+\delta }$ , where δ is a small positive smooth number.

The TV penalty is formulated as:

In Eq. [4], the derivative of image TV with respect to each pixel is expressed as:

where δ_TV is a small parameter to avoid instability induced by zero denominator. The flowchart of the joint L1 and TV regularized NCG algorithm (NCG_L1 + TV) is summarized as follow:

Algorithm 1 NCG_L1 + TV algorithm flowchart

1. Initial set: maximum iteration number k_max=20; backtracking line search parameters α=0.05 and β=0.6; initial reconstruction value $X_{L1+TV}^0=0$ ; initial search direction $d_0=-\nabla f(X_{L1+TV}^0)$ ; k=0.

2. Compute the step size: t_k=1, while $f(X_{L1+TV}^k+t_k{d}_k)>f(X_{L1+TV}^k)+\alpha t_k{d}_k\nabla f(X_{L1+TV}^k)$ , then t_k=βt_k.

3. Update reconstruction: $X_{L1+TV}^{k+1}=X_{L1+TV}^k+t_k{d}_k$

4. Update search direction: $d_{k+1}=-\nabla f(X_{L1+TV}^{k+1})+{\gamma }_k{d}_k$ ,${\gamma }_k={\Vert \nabla f(X_{L1+TV}^{k+1})\Vert }_2^2/{\Vert \nabla f(X_{L1+TV}^k)\Vert }_2^2$

5. k=k+1, if k>k_max stop iteration, otherwise go to step 2.

Owing to the ill-condition of the XFT reconstruction problem, the convergence speed of NCG_L1 + TV gradually slows down, making it difficult to achieve a satisfactory result. To remit this issue, we employed a restart strategy in this study. When the iteration number reaches k_max, the next search direction in NCG_L1 + TV is restarted as $-\nabla f(X_{L1+TV}^{k_{\max }+1})$ , rather than updated as $-\nabla f(X_{L1+TV}^{k_{\max }+1})+{\gamma }_k{d}_k$ as shown in Step 4 in Algorithm 1 scheme. And the negative values in $X_{L1+TV}^{k_{\max }}$ are set to zero, based on the non-negative constraint of XFT reconstruction. Then the non-negative $X_{L1+TV}^{k_{\max }}$ is used as the initial value for the next NCG_L1 + TV iteration. To increase the computational speed and reduce the memory consumption, we also reset the system matrix M by removing its columns corresponding to zero values in $X_{L1+TV}^{k_{\max }}$ . The workflow of restart NCG_L1 + TV algorithm (re_NCG_L1 + TV) is described in Figure 3A. Figure 3B shows the root mean square (RMS) error at different iterations. As illustrated, after several iterations, the change of RMS between two adjacent iterations is very small. In this work, the re_NCG_L1 + TV iteration process is terminated when the relative change of RMS is smaller than 1 percent.

Figure 3 Restart joint L1 and TV regularized NCG algorithm (re_NCG_L1 + TV). (A) Flowchart of re_NCG_L1 + TV; (B) the change of root mean square (RMS) error with the iteration number.

Comparison of reconstruction algorithms

FBP, ML-EM, L1 regularization and TV regularization methods were implemented to compare with the proposed L1 + TV regularization algorithm. To mitigate the effect of noise during reconstruction, an edge-preserving Gaussian filter was applied after each iteration in ML-EM algorithm (27). The L1 regularization and TV regularization were solved with a procedure similar to the re_NCG_L1 + TV algorithm, but with a different cost function. The L1 regularized reconstruction problem is expressed as:

And the TV regularized reconstruction problem is expressed as:

For the joint L1 and TV regularized reconstruction {Eq. [3]}, the regularization parameters λ_L1 and λ_TV were empirically set to 100 and 50, respectively. To maintain consistency in the iterative calculation and make a fair comparison, the λ_L1 parameter was also set to 100 in the L1 regularized reconstruction {Eq. [7]}, and the λ_TV parameter to 50 in the TV regularized reconstruction {Eq. [8]}.

The quality of reconstructed XFT images was assessed using CNR, DSC, and LE metrics (16,28). The CNR was calculated as:

where ROI and BKG are the target and background regions of the imaged object. S_ROI and S_BKG are the mean pixel values, δ_ROI and δ_BKG are the standard deviations in the ROI and BKG, respectively.

DSC was used to evaluate the similarity of the true and reconstructed targets, and was calculated as:

where ROI_r and ROI_t denote the regions of the reconstructed and true targets, respectively. And the notation $|\cdot |$ represents the cardinality of an ROI set.

LE was defined to evaluate the localization error of reconstructed targets:

where $L_{RO{I}_r}$ and $L_{RO{I}_t}$ denote the center of mass of the true and reconstructed targets located in the region ROI_r and ROI_t, respectively.

Radiation dose measurement

Gafchromic EBT2 films (Ashland, Covington, KY, USA) were used to measure the radiation dose. First, the film intensity was calibrated using 6 MV X-ray on a clinical linear accelerator (Varian, Palo Alto, CA, USA). The films were sandwiched in solid water slabs at 1.5 cm depth and irradiated with doses of 10, 20, 50, and then 1–16 Gy with a 1 Gy increment. The films were scanned 24 hours post irradiation, using the Epson Perfection V700 photo scanner (Epson, Long Beach, CA, USA). The film intensities were plotted against the corresponding doses and fitted with a fifth-order polynomial curve. Then, the water phantom with a film insert was positioned at the imaging isocenter of the dual-modality imaging system for radiation delivery. The X-ray tube was operated for 10 minutes in the CT or XFT setting as aforementioned to obtain the respective radiation dose rate.

Results

XRF Detection calibration

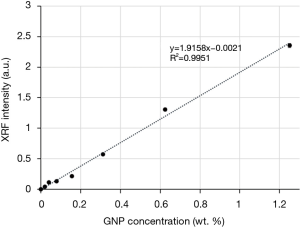
The signal intensity of the L-shell XRF as a function of GNP concentration (0.02–2.50 wt.%) is shown in Figure 4. The XRF intensity, measured over a sample volume of 0.5×0.5×2 mm³, was proportional to the true GNP concentration with R²>0.99, demonstrating the feasibility of quantitative measurement with our system. The detection limit, defined as the concentration corresponding to an XRF intensity that is 1.96 times of the standard deviation of the background (16), was calculated as 0.003 wt.%. This calculation was based on the linear fit shown in Figure 4 and the measured background intensity of 0.0014±0.0022 a.u.

Figure 4 The calibration curve depicting the XRF signal as a linear function of GNP concentration at 0.02, 0.08, 0.16, 0.31, 0.63, 1.25, and 2.50 wt.%. XRF, X-ray fluorescence; GNP, gold nanoparticles.

XFT imaging of the two-target phantom

An X-ray projection image and an axial CT slice of the water phantom containing 2 GNP vial inserts (0.08 and 0.16 wt.%) are shown in Figure 5A and B. The sinogram of the XFT acquisition is presented in Figure 5C. XFT images reconstructed using FBP, ML-EM, L1, TV and L1 + TV regularization methods are shown in Figure 5D. To better visualize image background noise, Figure 5D exhibits the histogram of noise in background region of interests marked in Figure 5B. Although FBP can recover the two GNP targets, there exist a lot of artifacts in the area adjacent to the targets and obvious target distortion. ML-EM mitigates the distortion and artifacts, and works much better than the FBP. However, there still exist some artifacts between the two targets, owing to the measured noise as shown in Figure 5C. The L1 regularization takes advantage of the sparsity penalty, and further mitigates the background artifact, but with poor edge preservation. In the TV regularized reconstruction, TV penalty can promote target smoothness and thus preserve the target edges. Nevertheless, there exists severe artifact between the two targets. In contrast, the joint L1 and TV regularization can reconstruct both targets with minimal background artifact while maximally restoring the target shape. As shown in Figure 5E, both L1 regularization and L1 + TV regularization present the smallest background noise. Compared with FBP and ML-EM, TV regularization presents background noise with higher mean value, however, with much smaller deviation, due to its superior performance in smoothness preservation.

Figure 5 Two-target phantom experiment. (A) A transmission X-ray projection image of the water phantom with two GNP vial inserts. (B) An axial CT slice of the water phantom. The GNP concentration was 0.16 and 0.08 wt.%, respectively. The solid/dotted circles denote the target/background regions of interest (ROI) for CNR calculation. (C) The sinogram for XFT reconstruction. (D) XFT images (top) and fused XFT/CT images (bottom) with XFT reconstructed using FBP, ML-EM, L1 regularization, TV regularization, and joint L1 + TV regularization methods. All XFT images were normalized to their own maximum. (E) Histograms of background noise in the BKG region shown in (B), for the XFT images reconstructed using different methods. XFT, X-ray fluorescence tomography; CNR, contrast-to-noise ratio; FBP, filtered back projection; GNP, gold nanoparticles.

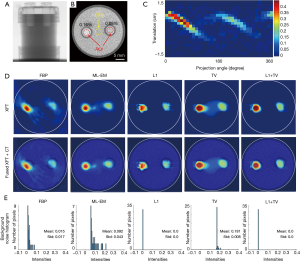
Table 1 summarizes the results of image quality evaluation. For CNR calculation, circular regions of interest ROI and BKG in Eq. [9] were placed within the GNP targets and at the center of the phantom, respectively, as shown in Figure 5B. The CT image provided the benchmark for the GNP target localization and distribution. To calculate DSC and LE, the reconstructed XFT image was equally divided into left and right halves, and then the target ROIs {i.e., ROI_r in Eqs. [10] and [11]} were defined after a threshold of 30% of the maximum in each half.

Table 1 Evaluation of the two-target XFT images reconstructed using 5 different methods
Full table

Both GNP targets in XFT images demonstrate higher CNR than their counterparts in CT, except for the 0.16 wt.% target in FBP reconstruction. As shown in Figure 5D, the reconstructed 0.16 wt.% target in FBP deviated from the true position, resulting in a small CNR. Compared with FBP, ML-EM shows higher CNR for the 0.16 wt.% target, but lower CNR for the 0.08 wt.% target, primarily because of the artifacts between the two targets. Both L1 regularization and TV regularization show higher CNR than ML-EM, owing to their superior performances in noise suppression and smoothness preservation, respectively. Compared with FBP, both L1 regularization and TV regularization show lower CNR for the 0.08 wt.% target, mainly owing to the poor target smoothness in L1 regularization and the high background noise in TV regularization. Combining the benefits of noise suppression and local smoothness preservation, L1 + TV regularization presents the highest CNR values. Moreover, with minimal artifact in the center region, L1 + TV regularization reconstructed both targets with a high localization precision and shape recovery accuracy. As reference, the DSC and LE of the CT was defined as 1 and 0, respectively.

XFT imaging of the four-target phantom

The structure of the four-target phantom is shown in the axial CT slice in Figure 6A. Figure 6B shows the sinogram for XFT reconstruction. XFT images reconstructed using different methods are shown in Figure 6C. Figure 6D shows the corresponding histograms of background noise. Similar to the results in the previous two-target experiment, L1 + TV regularization demonstrates the highest image quality, resulting from its superior performance in preserving target smoothness and suppressing background noise.

Figure 6 Four-target phantom experiment. (A) An axial CT slice of the water phantom with 4 GNP vial inserts. The GNP concentrations were 0.02, 0.04, 0.08 and 0.16 wt.%, respectively. (B) The sinogram for the four-target XFT reconstruction. The solid/dotted circles denote the target/background regions of interest (ROI) for CNR calculation. (C) XFT images (top) and fused XFT/CT images (bottom) with XFT reconstructed using FBP, ML-EM, L1, TV, and L1 + TV regularization methods. All the XFT images were normalized to their own maximum. (D) Histograms of background noise in the BKG region shown in (A), for the XFT images reconstructed using different methods. XFT, X-ray fluorescence tomography; CNR, contrast-to-noise ratio; FBP, filtered back projection; GNP, gold nanoparticles.

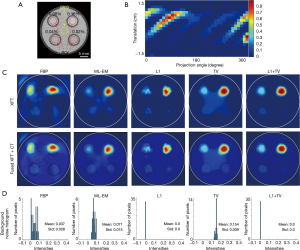
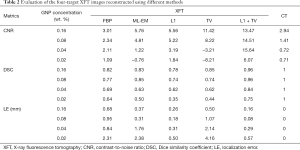
Table 2 lists the quantitative results of XFT image evaluation. The circular regions of ROI and BKG used for CNR calculation in Eq. [9] were placed within the targets and at the center of the phantom as shown in Figure 6A. To calculate DSC and LE, the XFT image was equally divided into four quarters, and ROI_r in Eqs. [10] and [11] were defined after a threshold of 30% of the maximum in each quarter.

Table 2 Evaluation of the four-target XFT images reconstructed using different methods
Full table

Due to the artifact at the center of phantom, the 0.04 and 0.02wt.% targets recovered using ML-EM and TV regularization methods had small or even negative CNR. Owing to their superior performance in noise suppression, the L1 and L1 + TV regularization methods present higher CNR values than the other 3 methods. Reducing GNP concentration deteriorates reconstruction accuracy, resulting in worse DSC and LE outcome. Nevertheless, L1 + TV regularization demonstrates highest image quality, with highest CNR values and submillimeter localization accuracy.

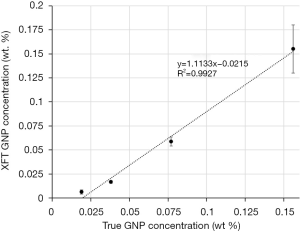
To validate the accuracy of L1 + TV regularization in quantifying GNP concentration, XFT image intensity was converted to GNP concentration using the calibration curve in Figure 4, and then correlated with the true GNP concentration. Figure 7 shows the relationship between the XFT and the true GNP concentration. The reconstructed GNP concentration is significantly proportional to the true concentration with R²>0.99.

Figure 7 Linear correlation between the XFT and true GNP concentration. XFT, X-ray fluorescence tomography; GNP, gold nanoparticles.

Radiation dose of the CT and XFT imaging

The dose rates measured at the imaging isocenter were 0.48 and 2.29 cGy/min, respectively, for the CT (45 kVp, 2.5 mA, 0.5 mm Cu filter) and XFT (64 kVp, 10 mA, 2 mm Al filter) setting. Taking into account the number of projections and the exposure time of each projection, the estimated imaging doses for CT and XFT were 0.35 and 41.22 cGy, respectively.

Discussion

The focus of this study was on the development of an effective regularization method for L-shell XFT reconstruction which is innately ill-posed owing to the high attenuation of excitation and fluorescence beams. First, a dual modality XFT/CT imaging system has been developed, where CT provides anatomy information and XFT realizes quantitative imaging of high-Z metal agents. Second, we developed a joint L1+ TV regularized XFT reconstruction algorithm. The L1 constraint was used to enhance sparsity and suppress noise, and the TV constraint to maintain the local smoothness and preserve the shape of targets. Multi-target imaging experiments validated the better performance of the joint L1 + TV regularization method over FBP, ML-EM, L1 regularization and TV regularization methods in target localization and shape recovery. Moreover, the highly linear correlation (R²>0.99) between the reconstructed and true GNP concentrations confirms the quantitative feature of the proposed method. In view of the analogous imaging mechanism, it is also expected that the proposed method will be applied in higher-energy K-shell XFT imaging.

In this study, we employed a single-pixel photon counting detector and pencil beam excitation, therefore the XFT scanning time was long, i.e., 6.3 hours to image one slice of a 3-cm-diameter phantom. The imaging time could be reduced dramatically by using detector array and volume excitation (29,30). Additionally, the imaging time could be further reduced by using semi-monochromatic excitation beam to increase the photon flux via an X-ray focus mirror (31). Nevertheless, the imaging setting in this study was sufficient to generate imaging data and evaluate reconstruction algorithms.

Under the current experimental setting, the estimated dose of XFT imaging is 41.22 cGy which is relatively high for in vivo small animal imaging. Further system optimization to shorten the acquisition time using detector array, as mentioned in previous discussion, can directly reduce the XFT imaging dose by multifold. Moreover, analogous to CT with limited-angle projections (32), limited-angle XFT imaging combined with an effective compressed sensing based reconstruction algorithm could also reduce imaging dose without sacrificing imaging quality.

A CNR of 3 was usually considered as the detectability threshold according to the Rose criterion (33). Based on this criterion, CT under the current setting showed a GNP detection limit of ~0.16 wt.% concentration. In contrast, XFT reconstructed with our proposed L1 + TV regularized algorithm showed a GNP detection limit of lower than 0.02 wt.%, about one order more sensitive than conventional CT.

To further evaluate the performance of the XFT/CT imaging system and regularization reconstruction algorithm, in vivo small animal studies will be conducted in the future. When applied to small animal imaging, the CT provides anatomy information, and the XFT provides distribution of imaged metal agents. Furthermore, the CT number can be used to correct the attenuation of both excitation X-ray beam and emission XRF, which is particularly useful in XFT imaging using low energy XRF.

Conclusions

We developed a dual-modality XFT/CT imaging system and a novel joint L1 and TV regularized XFT reconstruction method for quantitative GNP imaging. Our imaging study with multi-target phantoms demonstrated the superiority of the joint L1 and TV regularization method in noise suppression and shape preservation over FBP and ML-EM methods. Compared with other methods, the proposed L1 + TV regularization method recovered the targets with highest CNR and lowest LE (submillimeter accuracy). It can successfully recover the GNP distribution at 0.02 wt.% and even lower concentration level.

Acknowledgments

None.

Footnote

Conflicts of Interest: The authors have no conflicts of interest to declare.

References

1. Peer D, Karp JM, Hong S, Farokhzad OC, Margalit R, Langer R. Nanocarriers as an emerging platform for cancer therapy. Nat Nanotechnol 2007;2:751. [Crossref] [PubMed]
2. Jiao PF, Zhou HY, Chen LX, Yan B. Cancer-targeting multifunctionalized gold nanoparticles in imaging and therapy. Curr Med Chem 2011;18:2086-102. [Crossref] [PubMed]
3. Popovtzer R, Agrawal A, Kotov NA, Popovtzer A, Balter J, Carey TE, Kopelman R. Targeted gold nanoparticles enable molecular CT imaging of cancer. Nano Lett 2008;8:4593-6. [Crossref] [PubMed]
4. Giljohann DA, Seferos DS, Daniel WL, Massich MD, Patel PC, Mirkin CA. Gold nanoparticles for biology and medicine. Angew Chem Int Ed Engl 2010;49:3280-94. [Crossref] [PubMed]
5. Hainfeld JF, Slatkin DN, Smilowitz HM. The use of gold nanoparticles to enhance radiotherapy in mice. Phys Med Biol 2004;49:N309-15.
6. Jain S, Hirst DG, O'sullivan JM. Gold nanoparticles as novel agents for cancer therapy. Br J Radiol 2012;85:101-13. [Crossref] [PubMed]
7. Kim JK, Seo SJ, Kim KH, Kim TJ, Chung MH, Kim KR, Yang TK. Therapeutic application of metallic nanoparticles combined with particle-induced X-ray emission effect. Nanotechnology 2010;21:425102. [Crossref] [PubMed]
8. Huang X, El-Sayed IH, Qian W, El-Sayed MA. Cancer cell imaging and photothermal therapy in the near-infrared region by using gold nanorods. J Am Chem Soc 2006;128:2115-20. [Crossref] [PubMed]
9. Hainfeld JF, Smilowitz HM, O’connor MJ, Dilmanian FA, Slatkin DN. Gold nanoparticle imaging and radiotherapy of brain tumors in mice. Nanomedicine 2013;8:1601-9. [Crossref] [PubMed]
10. Eck W, Nicholson AI, Zentgraf H, Semmler W, Bartling S. Anti-CD4-targeted gold nanoparticles induce specific contrast enhancement of peripheral lymph nodes in X-ray computed tomography of live mice. Nano Lett 2010;10:2318-22. [Crossref] [PubMed]
11. Hainfeld JF, O’Connor MJ, Dilmanian FA, Slatkin DN, Adams DJ, Smilowitz HM. Micro-CT enables microlocalisation and quantification of Her2-targeted gold nanoparticles within tumour regions. Br J Radiol 2011;84:526-33. [Crossref] [PubMed]
12. Ricketts K, Guazzoni C, Castoldi A, Gibson AP, Royle GJ. An X-ray fluorescence imaging system for gold nanoparticle detection. Phys Med Biol 2013;58:7841. [Crossref] [PubMed]
13. Kuang Y, Pratx G, Bazalova M, Meng B, Qian J, Xing L. First demonstration of multiplexed X-ray fluorescence computed tomography (XFCT) imaging. IEEE Trans Med Imaging 2013;32:262-7. [Crossref] [PubMed]
14. Larsson JC, Carmen V, William V, Muhammet ST, Johanna D, Marie AH, Hans MH. High-spatial-resolution X-ray fluorescence tomography with spectrally matched nanoparticles. Phys Med Biol 2018;63:164001. [Crossref] [PubMed]
15. Manohar N, Reynoso FJ, Diagaradjane P, Krishnan S, Cho SH. Quantitative imaging of gold nanoparticle distribution in a tumor-bearing mouse using benchtop X-ray fluorescence computed tomography. Sci Rep 2016;6:22079. [Crossref] [PubMed]
16. Manohar N, Reynoso FJ, Cho SH. A benchtop cone-beam X-ray fluorescence computed tomography (XFCT) system with a high-power X-ray source and transmission CT imaging capability. Med Phys 2018;45:4652-9. [Crossref] [PubMed]
17. Cheong SK, Jones BL, Siddiqi AK, Liu F, Manohar N, Cho SH. X-ray fluorescence computed tomography (XFCT) imaging of gold nanoparticle-loaded objects using 110 kVp X-rays. Phys Med Biol 2010;55:647. [Crossref] [PubMed]
18. Bazalova-Carter M, Ahmad M, Xing L, Fahrig R. Experimental validation of L-shell X-ray fluorescence computed tomography imaging: phantom study. Journal of Medical Imaging 2015;2:043501. [Crossref] [PubMed]
19. Manohar N, Reynoso FJ, Cho SH. Experimental demonstration of direct L-shell X-ray fluorescence imaging of gold nanoparticles using a benchtop X-ray source. Med Phys 2013;40:080702. [Crossref] [PubMed]
20. Bazalova-Carter M. The potential of L-shell X-ray fluorescence CT (XFCT) for molecular imaging. Br J Radiol 2015;88:20140308. [Crossref] [PubMed]
21. Bazalova M, Ahmad M, Pratx G, Xing L. L-shell X-ray fluorescence computed tomography (XFCT) imaging of Cisplatin. Phys Med Biol 2014;59:219. [Crossref] [PubMed]
22. Donoho DL. Compressed sensing. IEEE Trans Inf Theory 2006;52:1289-306. [Crossref]
23. Rudin LI, Osher S, Fatemi E. Nonlinear total variation based noise removal algorithms. Physica D: Nonlinear Phenomena 1992;60:259-68. [Crossref]
24. Lustig M, Donoho D, Pauly JM. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magn Reson Med 2007;58:1182-95. [Crossref] [PubMed]
25. Feldkamp LA, Davis LC, Kress JW. Practical cone-beam algorithm. Journal of the Optical Society of America A 1984;1:612-9. [Crossref]
26. Ricketts K, Castoldi A, Guazzoni C, Ozkan C, Christodoulou C, Gibson AP, Royle GJ. A quantitative X-ray detection system for gold nanoparticle tumour biomarkers. Phys Med Biol 2012;57:5543. [Crossref] [PubMed]
27. Slijpen ET, Beekman FJ. Comparison of post-filtering and filtering between iterations for SPECT reconstruction. IEEE Transactions on Nuclear Science 1999;46:2233-8. [Crossref]
28. Shi J, Udayakumar TS, Wang Z, Dogan N, Pollack A, Yang Y. Optical molecular imaging-guided radiation therapy part 1: Integrated X-ray and bioluminescence tomography. Med Phys 2017;44:4786-94. [Crossref] [PubMed]
29. Li L, Zhang S, Li R, Chen Z. Full-field fan-beam X-ray fluorescence computed tomography with a conventional X-ray tube and photon-counting detectors for fast nanoparticle bioimaging. Optical Engineering 2017;56:043106. [Crossref]
30. Jones BL, Manohar N, Reynoso F, Karellas A, Cho SH. Experimental demonstration of benchtop X-ray fluorescence computed tomography (XFCT) of gold nanoparticle-loaded objects using lead-and tin-filtered polychromatic cone-beams. Phys Med Biol 2012;57:N457-67.
31. Hertz HM, Larsson JC, Lundström U, Larsson DH, Vogt C. Laboratory X-ray fluorescence tomography for high-resolution nanoparticle bio-imaging. Opt Lett 2014;39:2790-3. [Crossref] [PubMed]
32. Chen GH, Tang J, Leng S. Prior image constrained compressed sensing (PICCS): a method to accurately reconstruct dynamic CT images from highly undersampled projection data sets. Med Phys 2008;35:660-3. [Crossref] [PubMed]
33. Rose A. Vision: Human and Electronic. New York/London: Plenum Press, 1973.