
Probability-based 3D k-space sorting for motion robust 4D-MRI
Introduction
Primary liver cancer and liver metastases are the main causes of worldwide cancer morbidity and mortality. The difficulty of treating abdominal tumor sites is exacerbated by respiratory motion within thoracic and abdominal regions (1,2). 4D-CT is the current clinical standard for imaging respiratory motion in radiation therapy. However, several limitations have restricted the application of 4D-CT imaging in abdominal cancers, including low soft tissue contrast and susceptibility to artifacts such as blurring, duplication, overlapping, and incompletion (1,2) during data acquisition and post processing. 4D-MRI techniques have been recently developed to overcome the aforementioned limitations of 4D-CT in abdominal imaging (1-8). A detailed review and summary of recent 4D-MRI studies is presented in the literature (1,2).
Most of the 4D-MRI techniques reported so far use the retrospective approach to sort and reconstruct 4D-MRI images. Depending upon the MRI acquisition scheme used, retrospective sorting (9) is applied either to the images (for 2D acquisition) or to the k-space data (for 3D acquisition). While both acquisition schemes have been shown to be effective in obtaining organ respiratory motion information with good tempo-spatial resolution (9-12), they are affected by breathing variations, causing motion artifacts in the resulting 4D-MRI images. It has been demonstrated that the most significant impacts on 4D-MRI image quality due to motion are aliasing artifacts in the anterior-posterior (AP) direction. The clinical impact of real noise in 4D-MRI images as it affects region of interest (ROI) delineation and motion estimation have not yet been fully evaluated in patient studies (10). The breathing-variation-induced motion artifacts, often manifested as tissue discontinuities in 2D acquisitions and as ghosting and blurring artifacts in 3D acquisitions, degrade the image quality of 4D-MRI and can adversely affect its radiation therapy applications. Many studies have shown that these breathing variations can adversely affect image quality, target-volume determination, dose delivery, and patient positioning (13-16). Although it has been shown that sequential-mode 4D-MRI provides more accurate motion measurement than conventional cine-mode 4D-MRI, the image quality has only been evaluated in the superior-inferior (SI) direction in terms of respiratory motion accuracy. Tumor contrast and target volume have not been investigated (16), and motion artifacts caused by breathing variation have not been carefully addressed yet.
To tackle the problem of breathing-variation-induced motion artifacts (e.g., noise), we have recently developed a novel probability-based sorting method that inherently incorporates breathing variations in the sorting process and 4D-MRI reconstruction. We have shown that this new method can effectively reduce breathing-variation-induced motion artifacts (1,2). In addition, this method can generate multiple sets of 4D-MRI images that represent the main breathing patterns of the patient.
Using a similar approach as described in previous work of image-space probability-based multi-cycle 4D MRI (17), we first decompose the breathing signal to determine the main breathing cycles and for each main breathing cycle we reconstruct a set of 4D-MRI images by sorting the k-space data using the result-driven method (18). Both 3D k-space phase sorting and 3D k-space probability-based multi-cycle sorting methods can potentially improve image quality as compared to the current image-space based 4D-MRI techniques. Furthermore, the new 4D-MRI technique can be implemented theoretically on any MR sequence, eliminating the requirement for high image acquisition speed as in the image-space based 4D-MRI techniques. As a result, some of the slow but high-quality MR sequences such as the T2-w fast spin echo (FES) MR sequence which is characterized by high tumor contrast can be used for 4D-MRI development, potentially enhancing the final image quality of 4D-MRI. The feasibility of this proposed novel 3D k-space probability-based multi-cycle sorting method was verified by applying patients’ respiratory signals on a 4D-extended cardiac-torso (XCAT) phantom. The effectiveness of this method was shown by comparing the quality and tumor motion management of acquired images with those obtained through 3D k-space phase-based sorting method.
To better understand the relationships between motion artifacts and breathing irregularity for developing the multi-cycle 4D-MRI method, we first studied 4D-MRI motion artifacts in cases of 2D acquisition and 3D acquisition using the phase-based single-cycle sorting method. An irregular breathing curve of a real patient and an artificially generated regular cosine curve were tested in a simulation study using the 4D XCAT phantom (19). The 4D-MRI motion artifacts were evaluated qualitatively for these two curves. It was found during the study that apparent motion artifacts existed unexpectedly for the regular cosine curve. This phenomenon was further investigated to identify the potential cause of intra-phase breathing motion in this scenario.
Methods
The general method of probability-based sorting method for multi-cycle 4D-MRI reconstruction has been described in our previous study (17). In that study, the method was applied to 2D MR acquisitions (cine and sequential) for 4D-MRI sorting and the results demonstrate that this method not only produces multi-cycle 4D-MRI images that represent the main breathing patterns of the patient, but also reduces breathing variation artifacts in each 4D-MRI image set. In addition, it also improves the accuracy of tumor motion probability density function (PDF) estimates and the average intensity projection (AIP) of the 4D-MRI images.
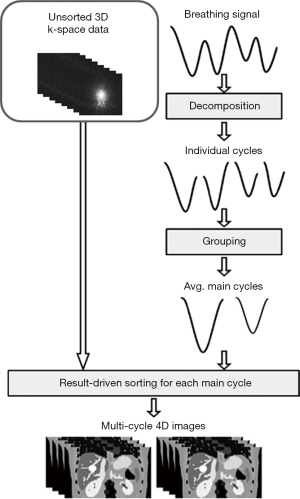
Probability-based 3D k-space sorting for multi-cycle 4D-MRI
The design and workflow of the probability-based 3D k-space sorting method for multi-cycle 4D-MRI, as shown in Figure 1, is adapted from the probability-based 2D image sorting method for multi-cycle 4D-MRI (17) with two major alterations: (I) sorting is performed on 3D k-space data instead of 2D MR images; (II) MR images are reconstructed using the fast Fourier transform (FFT) after 3D k-space sorting (18), whereas this was unnecessary in the previous study as the MR images had already been reconstructed. A detailed review of the probability-based sorting method can be found in the literature (17) and thus will only be briefly described here. The main breathing cycles of the breathing curves were extracted using principle component analysis (PCA) method: Firstly, the breathing signal is decomposed into individual breathing cycles, which are defined as segments of the breathing signal between two consecutive end-of-exhale (EOE) peaks. Each individual breathing cycle is characterized by its amplitude (A) and period (T). Secondly, individual breathing cycles are grouped based on their amplitudes and periods to determine the main breathing cycles which represent the patient’s main breathing patterns. Practically, if the mean breathing period is less than or equal to 4 s, the period (T) bin size is set to be 0.5 s, otherwise, 1 s. The amplitude range that a group covers for different patient is selected in such a way that 95% of the data points fall in 20% of the displacement range, to accommodate the potential large variation of the breathing amplitude among patients. A main breathing cycle is determined as the average of individual breathing cycles in a group which contains more that 10% of the total number of breathing cycles in a breathing signal. The main breathing cycles are then characterized by motion trajectory, period, amplitude and frequency of occurrence. In practical analysis, the abnormal breathing variations should be excluded, and the number of main breathing cycles should be limited (<4) for reasonable image acquisition time. Finally, a set of 4D-MRI images is reconstructed for each main breathing cycle using a result-driven sorting method (18). Briefly, the result-driven approach was developed for better utilization of redundant images when multiple images were assigned to a bin. The mean breathing trajectory is firstly calculated from the entire breathing signal as the targeted motion. The amplitude of a bin is then identified as the amplitude of the mean breathing trajectory at the center of a bin. The image data with the amplitude closest to the amplitude of this bin is finally chosen to generate the 4D-MRI in each bin.
Digital phantom study
The probability-based 3D k-space sorting method for multi-cycle 4D-MRI was tested on the 4D XCAT digital human phantom (19). The motion of the 4D-XCAT phantom was driven by a given respiratory curve to generate 3D volumes of MR images. The respiratory motion is controlled by two-time curves: one defines the change of the diaphragm height and the other defines the amount of AP expansion of the chest. The parameters are controlled and hard coded in the XCAT phantom so that the other organs aside from the target organ move in the manner that they don’t collide (19). A hypothetic tumor of 30 mm in diameter was inserted in the liver of the XCAT phantom. The 4D-MRI acquisition was simulated by continuously generating and extracting k-space data from the 4D-XCAT images based on a 3D Cartesian sampling scheme. The extracted k-space data was sorted based on respiratory phases and then converted to different phase images using 3D inverse fast Fourier transform (3D-IFFT), producing the simulated 4D-MRI images.
For comparison, the conventional phase sorting method was also simulated using the same 4D-XCAT digital phantom to generate a single-cycle 4D-MRI. Signal-to-noise ratio (SNR) of tumor and liver, tumor volume consistency, and AIP images were determined and compared between the conventional phase sorting method and the new probability-based sorting method. The original 4D-XCAT images were used as reference for the comparisons. Though MR images have been widely used for tumor delineation, AIP is more suitable for dose calculation in clinical practice, since it can represent tissue motion probability and is often used for treatment planning and image guidance. For MRI or MRI-based radiation therapy, better AIP means more accurate prediction of synthetic CT from MRI.
To evaluate tumor volume consistency, tumor volumes at 10 respiratory phases of 4D-MRI were measured and compared. The ten tumor volumes were normalized to the maximum tumor volume of the ten, and the standard deviation (SD) of the ten tumor volumes was calculated.
AIP images for the simulated single-cycle 4D-MRI, the simulated multi-cycle 4D-MRI, and the original 4D-MRI (4D-XCAT) were also compared. In particular, the AIP for the multi-cycle 4D-MRI was generated by incorporating the weightings and breathing periods of the multiple breathing cycles as described by the following equation (17):
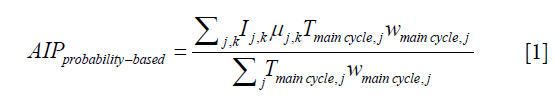
where, Tmain cycle,j and wmain cycle,j are the period and the weighting (frequency of occurrence) of the jth main cycle; Ij,k is the 3D image volume at the kth amplitude bin of the jth main cycle; and µj,k is the ratio of the time interval at the kth amplitude bin in the jth main cycle to the jth main cycle period, Tmain cycle,j. Furthermore, the difference maps between the reference AIP (from the original 4D-MRI/4D-XCAT) and the two AIPs under evaluation (from single-cycle 4D-MRI and multi-cycle 4D-MRI) were determined as (17):
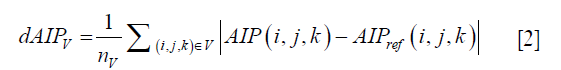
where dAIPV is the AIP difference in image volume, nV is the number of voxels in that image volume, AIP (i, j, k) and AIPref (i, j, k) are the intensities of AIP at coordinate (i, j, k) in reconstructed images and reference images, respectively.
In this study, we tested a real patient’s breathing curve and an artificially generated breathing curve composed of two main cycles whose breathing characteristics (time weighting, breathing amplitude and breathing period) were (50%, 14.5 mm, 2.77 s) and (50%, 30.0 mm, 2.25 s) for the two cycles, respectively.
Results
4D-MRI motion artifacts in single-cycle 3D k-space sorting
Figure 2 shows the comparison between 4D-MRI images reconstructed using 2D image sorting (for 2D MR acquisition) and 3D k-space sorting (for 3D MR acquisition). The same real patient’s breathing curve was used for XCAT 4D-MRI simulation. Breathing variation induced motion artifacts exist in both 4D-MRI images, but are presented as tissue discontinuities in 2D image sorting, and as ghost and blurring artifacts in 3D k-space sorting. The ‘tumor’ appears clear but broken in the 2D case, while blurry but complete in the 3D case. Measurement of tumor volumes in the 4D-MRI images showed that 3D k-space sorting had smaller inter-phase tumor volume variation (thus better inter-phase tumor volume consistency) as compared to 2D image sorting: the SD of tumor volumes is 0.0720 and 0.1149 for 3D k-space sorting and 2D image sorting, respectively.
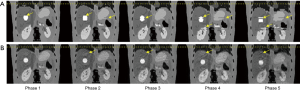
Figure 3 shows the 4D-MRI [end-of-inhale (EOI) phase] motion artifacts due to intra-phase variation. A cosine curve (i.e., regular breathing pattern) is used in this XCAT 4D-MRI simulation. Despite the regular breathing pattern, motion artifacts (image blurring) still exist in the 4D-MRI images due to intra-phase variation, although the level is reduced when compared to the artifacts detected using the irregular patient curve (as shown in Figure 2). It can also be seen that the motion artifacts are reduced when the intra-phase variation is small.

Probability-based 3D k-space sorting for multi-cycle 4D-MRI
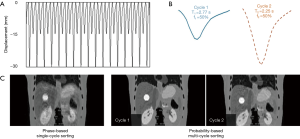
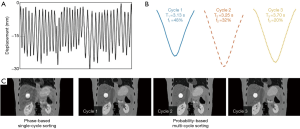
Figure 4 shows the 4D-MRI images (EOI phase only) reconstructed using the phase-based single-cycle sorting method and the probability-based multi-cycle sorting method for an artificial curve (Figure 4A), the two main cycles (cycle 1 and cycle 2 in Figure 4B) were extracted based on PCA analysis and the corresponding 4D-MRI images (Figure 4C) for each cycle were then generated. Figure 5 shows the 4D-MRI images (EOI phase only) reconstructed using the phase-based single-cycle sorting method and the probability-based multi-cycle sorting method for a patient curve (Figure 5A), the three main cycles (cycle 1, cycle 2, and cycle 3 in Figure 5B) were extracted based on PCA analysis and the corresponding 4D-MRI images (Figure 5C) for each cycle were then generated. In both cases, the probability-based method produced 4D-MRI images with significantly reduced motion artifacts (i.e., less blurring) as compared to the conventional phase-based method.
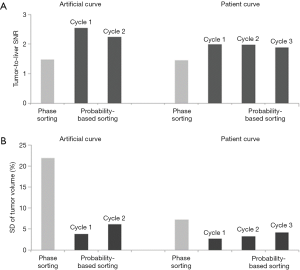
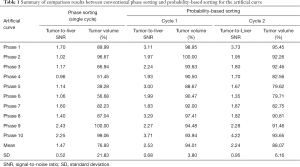
Tumor-to-liver SNR and tumor volume at each of 10 phases of 4D-MRI for both sorting methods for the artificial curve and the patient curve, and their mean values and SDs are shown in Figure 6. It is clearly seen that tumor-to-liver SNR was noticeably improved and the tumor volume variation was largely reduced (i.e., tumor volume consistency improved) by the probability-based sorting method as compared to the phase sorting method for both the artificial-curve and patient-breathing-curve cases. The quantitative results are summarized in Table 1 and Table 2 for the artificial curve and the patient curve, respectively.
Full table
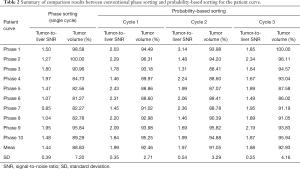
Full table
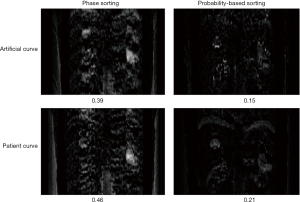
Figure 7 shows the AIP difference maps between the reconstructed 4D-MRI AIP and the reference 4D-XCAT AIP for the phase sorting method and the probability-based sorting method. It is clearly seen that for both the artificial curve (top row) and the patient curve (bottom row), the difference intensity is apparently reduced by the probability-based sorting method as compared to the phase sorting method: the average intensity difference per voxel is reduced from 0.39 to 0.15 for the artificial curve, and from 0.46 to 0.21 for the patient curve. These results imply that more accurate AIP results can be achieved using the probability-based sorting method than the phase sorting method.
Discussion
In this study, we demonstrated the method and the application of probability-based sorting for a 4D-MRI technique that is based on 3D acquisition. Compared to conventional phase-based sorting, the new method is advantageous in generating multi-cycle 4D-MRI images with improved image quality by reducing breathing-variation-induced motion artifacts. The advantages of the new method were successfully illustrated in the digital phantom study in which the new method showed significant improvements in SNRs of tumor and liver, inter-phase tumor volume consistency, and accuracy of AIPs. This work is an extension of, but more complicated than, our previous work in which the probability-based sorting was applied to a 4D-MRI technique that was based on 2D MR acquisitions (17). In previous work the sorting is performed on 2D images and the motion artifact is tissue discontinuity, while in current work the sorting is performed on 3D k-space data and the motion artifacts are ghosting and blurring. Through these two studies we have demonstrated that the probability-based sorting can be applied to different types of 4D-MRI techniques, based on either 2D acquisition or 3D acquisition, to improve the image quality of 4D-MRI via simultaneous motion artifacts reduction and multi-cycle reconstruction. The improved 4D-MRI can then be used to more accurately determine tumor volumes such as internal target volume (ITV) and more accurately calculate radiation dose in MRI-based treatment planning.
It is true that the k-space lines within similar breathing cycles can be used to reconstruct better 4D-MRI in single-cycle phase sorting method. However, much more data and undesired longer acquisition time are needed since the irregular breathing data cannot be used for reconstruction. Most importantly, the single-cycle 4D-MRI does not accurately reflect true patient breathing variation. Compared to the conventional single-cycle phase sorting method, the probability-based multi-cycle sorting method requires only a slightly longer imaging time to obtain complete respiratory information of different breathing patterns and relatively more data acquisition to fill in the additional amplitude bins reside in multiple main cycles. However, since part of the data (e.g., data at the EOE phase) can be shared by different breathing cycles and regular and irregular breathing data can be utilized for multi-cycle 4D-MRI reconstruction to boost data usage in probability-based sorting, the added imaging time accounts for only a small portion (~30%) of the entire imaging time, without significantly increasing the total image acquisition time, meanwhile, breathing variation information can be inherently embedded. Furthermore, there are various fast MR imaging and reconstruction methods, such as view sharing (20-22), compressed sensing (23-26), and iterative reconstruction (27-29), that can be applied to accelerate 4D-MRI. It is expected that the combination of probability-based sorting and fast MR imaging has the potential to reduce image acquisition time and further improve image quality of 4D-MRI. Furthermore, though we demonstrated the Cartesian acquisition in this study, the application of probability-based sorting method can be readily extended to other acquisition schemes (e.g., radial, spiral, pseudo-random, etc.) in MRI, since they meet the same criteria that is required for probability-based sorting, that the k-space data segments are randomly assigned to different respiratory phases, where the breathing variation is inherently incorporated in the sorting process. Moreover, our method can be generalized to the imaging of other anatomical structures since it was based on digital human phantom and the parameters of the tumor and its adjacent organs and the motion pattern were generated artificially. We were focusing on the study and the analysis of the motion and the artifact, rather than the organ type. Therefore, our method is not organ-specific. If the k-space data and the breathing signal could be recorded simultaneously, our method can be applied to any motional organs within the abdominal region (e.g., liver, pancreas, etc.).
There are several limitations in our study. Firstly, although we demonstrated the presence of residual motion artifacts caused by intra-phase breathing variation, we did not provide a solution to resolve this problem. We have tested, however, that uneven k-space acquisition (such as more samplings near k-space center) together with view sharing can reduce the effects of intra-phase breathing variation. It is expected that non-Cartesian acquisitions are less affected by the intra-phase breathing variation than Cartesian acquisition due to its dense sampling near k-space center. Secondly, we only simulated a simple Cartesian acquisition in this study. The probability-based sorting can also be applied to other more complicated Cartesian acquisitions [such as echo-planar imaging (EPI)] and non-Cartesian acquisitions (such as spiral and radial) using the same principle as illustrated in this study, although the sorting algorithm and image reconstruction will be different and will need to be optimized depending upon the acquisition scheme. Thirdly, we have only performed simulations on a digital human phantom in this study. Evaluation and validation of the new method on cancer patients are necessary for a comprehensive evaluation of its real clinical efficacy. This will be the topic of our future studies. Additionally, we have identified some ways in which, machine learning can enhance our research goals and we intend to pursue some of these ideas imminently: firstly, machine learning can be used in the analysis of the PDF, to generate more accurate and robust tumor motion PDF, and to extract the main cycles of patients’ breathing curves. Secondly, artificial neural networks can be trained to minimize the intra-phase variation-caused motion artifact by adaptively optimizing the phase bin size and the amplitude bin size. Thirdly, machine learning can be of great help in noise reduction to make the images even better. Fourthly, pattern recognition and segmentation generated by machine learning can potentially improve treatment planning.
Conclusions
This study successfully demonstrated the application of probability-based k-space sorting for a 4D-MRI technique based on 3D image acquisition. This new sorting method is superior to the conventional phase-based sorting method as it can generate multi-cycle 4D-MRI images with improved image quality by reducing breathing variation induced motion artifacts. The generality and robustness of this new 4D-MRI method warrants further evaluation in patients and for different types of 3D MR sequences.
Acknowledgments
Funding: This work is partly supported by funding from NIH (1R21CA165384 and 1R21CA195317).
Footnote
Conflicts of Interest: The authors have no conflicts of interest to declare.
References
- Cai J, Read PW, Altes TA, Molloy JA, Brookeman JR, Sheng K. Evaluation of the reproducibility of lung motion probability distribution function (PDF) using dynamic MRI. Phys Med Biol 2007;52:365-73. [Crossref] [PubMed]
- Cai J, Read PW, Larner JM, Jones DR, Benedict SH, Sheng K. Reproducibility of interfraction lung motion probability distribution function using dynamic MRI: statistical analysis. Int J Radiat Oncol Biol Phys 2008;72:1228-35. [Crossref] [PubMed]
- Pan T, Lee TY, Rietzel E, Chen GT. 4D-CT imaging of a volume influenced by respiratory motion on multi-slice CT. Med Phys 2004;31:333-40. [Crossref] [PubMed]
- Brandner ED, Wu A, Chen H, Heron D, Kalnicki S, Komanduri K, Gerszten K, Burton S, Ahmed I, Shou Z. Abdominal organ motion measured using 4D CT. Int J Radiat Oncol Biol Phys 2006;65:554-60. [Crossref] [PubMed]
- Betancourt R, Zou W, Plastaras JP, Metz JM, Teo BK, Kassaee A. Abdominal and pancreatic motion correlation using 4D CT, 4D transponders, and a gating belt. J Appl Clin Med Phys 2013;14:4060. [Crossref] [PubMed]
- Kwong Y, Mel AO, Wheeler G, Troupis JM. Four-dimensional computed tomography (4DCT): A review of the current status and applications. J Med Imaging Radiat Oncol 2015;59:545-54. [Crossref] [PubMed]
- Bouilhol G, Ayadi M, Rit S, Thengumpallil S, Schaerer J, Vandemeulebroucke J, Claude L, Sarrut D. Is abdominal compression useful in lung stereotactic body radiation therapy? A 4DCT and dosimetric lobe-dependent study. Phys Med 2013;29:333-40. [Crossref] [PubMed]
- Zhang L, Xi M, Deng XW, Li QQ, Huang XY, Liu MZ. Four-dimensional CT-based evaluation of volumetric modulated arc therapy for abdominal lymph node metastasis from hepatocellular carcinoma. J Radiat Res 2012;53:769-76. [Crossref] [PubMed]
- Paganelli C, Kipritidis J, Lee D, Baroni G, Keall P, Riboldi M. Image-based retrospective 4D MRI in external beam radiotherapy: A comparative study with a digital phantom. Med Phys 2018;45:3161-72. [Crossref] [PubMed]
- Liu Y, Yin FF, Chen NK, Chu ML, Cai J. Four dimensional magnetic resonance imaging with retrospective k-space reordering: a feasibility study. Med Phys 2015;42:534-41. [Crossref] [PubMed]
- Breuer K, Meyer CB, Breuer FA, Richter A, Exner F, Weng AM, Ströhle S, Polat B, Jakob PM, Sauer OA, Flentje M, Weick S. Stable and efficient retrospective 4D-MRI using non-uniformly distributed quasi-random numbers. Phys Med Biol 2018;63:075002. [Crossref] [PubMed]
- Kellman P, Chefd'hotel C, Lorenz CH, Mancini C, Arai AE, McVeigh ER. High spatial and temporal resolution cardiac cine MRI from retrospective reconstruction of data acquired in real time using motion correction and resorting. Magn Reson Med 2009;62:1557-64. [Crossref] [PubMed]
- De Ponti E, Prati G, Morzenti S, Zorz A, Guerra L, Crivellaro C, Arosio M, Crespi A. Relationship between image quality and patient’s respiratory pattern in 4D PET/CT protocols. J Nucl Med 2014;55:2058.
- Kamomae T, Monzen H, Nakayama S, Mizote R, Oonishi Y, Kaneshige S, Sakamoto T. Accuracy of image guidance using free-breathing cone-beam computed tomography for stereotactic lung radiotherapy. PLoS One 2015;10:e0126152. [Crossref] [PubMed]
- Cooper BJ, O'Brien RT, Kipritidis J, Shieh CC, Keall PJ. Quantifying the image quality and dose reduction of respiratory triggered 4D cone-beam computed tomography with patient-measured breathing. Phys Med Biol 2015;60:9493-513. [Crossref] [PubMed]
- Liu Y, Yin FF, Rhee D, Cai J. Accuracy of respiratory motion measurement of 4D-MRI: A comparison between cine and sequential acquisition. Med Phys 2016;43:179. [Crossref] [PubMed]
- Liang X, Yin FF, Liu Y, Cai J. A probability-based multi-cycle sorting method for 4D-MRI: A simulation study. Med Phys 2016;43:6375. [Crossref] [PubMed]
- Liu Y, Yin FF, Czito BG, Bashir MR, Cai J. T2-weighted four dimensional magnetic resonance imaging with result-driven phase sorting. Med Phys 2015;42:4460-71. [Crossref] [PubMed]
- Segars WP, Sturgeon G, Mendonca S, Grimes J, Tsui BM. 4D XCAT phantom for multimodality imaging research. Med Phys 2010;37:4902-15. [Crossref] [PubMed]
- Saranathan M, Rettmann DW, Hargreaves BA, Clarke SE, Vasanawala SS. DIfferential Subsampling with Cartesian Ordering (DISCO): a high spatio-temporal resolution Dixon imaging sequence for multiphasic contrast enhanced abdominal imaging. J Magn Reson Imaging 2012;35:1484-92. [Crossref] [PubMed]
- Deshmane A, Gulani V, Griswold MA, Seiberlich N. Parallel MR imaging. J Magn Reson Imaging 2012;36:55-72. [Crossref] [PubMed]
- Krishnamurthy R, Bahouth SM, Muthupillai R. 4D Contrast-enhanced MR Angiography with the Keyhole Technique in Children: Technique and Clinical Applications. Radiographics 2016;36:523-37. [Crossref] [PubMed]
- Jaspan ON, Fleysher R, Lipton ML. Compressed sensing MRI: a review of the clinical literature. Br J Radiol 2015;88:20150487. [Crossref] [PubMed]
- Haldar JP, Hernando D, Liang ZP. Compressed-sensing MRI with random encoding. IEEE Trans Med Imaging 2011;30:893-903. [Crossref] [PubMed]
- Gamper U, Boesiger P, Kozerke S. Compressed sensing in dynamic MRI. Magn Reson Med 2008;59:365-73. [Crossref] [PubMed]
- Lustig M, Donoho D, Pauly JM. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magn Reson Med 2007;58:1182-95. [Crossref] [PubMed]
- Block KT, Uecker M, Frahm J. Model-based iterative reconstruction for radial fast spin-echo MRI. IEEE Trans Med Imaging 2009;28:1759-69. [Crossref] [PubMed]
- Block KT, Uecker M, Frahm J. Undersampled radial MRI with multiple coils. Iterative image reconstruction using a total variation constraint. Magn Reson Med 2007;57:1086-98. [Crossref] [PubMed]
- Sutton BP, Noll DC, Fessler JA. Fast, iterative image reconstruction for MRI in the presence of field inhomogeneities. IEEE Trans Med Imaging 2003;22:178-88. [Crossref] [PubMed]


