
Accelerating the 3D T1ρ mapping of cartilage using a signal-compensated robust tensor principal component analysis model
Introduction
Osteoarthritis (OA) is an important public health problem (1,2). Cartilage degeneration due to OA changes the functional properties of cartilage and can eventually cause cartilage destruction (3). Conventional magnetic resonance imaging (MRI) provides sufficient tissue contrast to detect morphological changes in cartilage (4) but cannot measure the physiological changes in cartilage that occur during the earliest stages of OA development (2,5). Recent studies have shown that quantitative MRI has the potential to serve as a reproducible, noninvasive biomarker to identify subjects at risk for OA (6,7).
Magnetic spin-lattice relaxation in the rotating frame (T1ρ) has received considerable interest in the early detection of cartilage degeneration (8,9). It can probe the slow motion of the macromolecules in the articular cartilage extracellular matrix (ECM). Changes to the ECM, such as proteoglycan loss, can be reflected in the T1ρ measurements (10). In vivo studies have shown that the cartilage T1ρ value increased in OA subjects compared with controls (11-13). Furthermore, elevated T1ρ was observed in subcompartments in OA subjects where no obvious morphological changes were observed, suggesting the capability of T1ρ in detecting very early biochemical changes within the cartilage matrix (12).
Quantitative T1ρ imaging suffers from a long scan time since multiple T1ρ-weighted images with different spin-lock times (TSLs) must be acquired to calculate the T1ρ values. Relative to 2D T1ρ mapping, 3D T1ρ mapping is more suitable for cartilage imaging because of the small size of the articular cartilage. However, using 3D imaging further prolongs the scan time and thus limits the widespread clinical use of this technique. Therefore, it is necessary to accelerate the data acquisition for 3D T1ρ mapping of cartilage.
Several methods based on compressed sensing (CS) have been proposed for 3D T1ρ mapping acceleration (14-19). Due to the high compressibility of the image in the parametric direction, CS is especially suitable for T1ρ mapping. Pandit et al. combined CS with data-driven parallel imaging (PI) to accelerate cartilage T1ρ mapping and successfully implemented the data acquisition process on a clinical MRI scanner. The scan time was reduced to one-third that associated with full sample acquisition (14). Zhou et al. reconstructed the undersampled T1ρ mapping data using the combined CS and PI method and achieved acceleration factors of 3 and 3.5. However, this technique has been applied only in a 2D version of the reconstruction scheme (18). Zibetti et al. compared the results with reconstructions of 3D T1ρ images based on CS using different regularization functions and achieved a very high acceleration factor of 10 for both Cartesian and radial acquisitions (16,19). They recommended the low-rank plus sparse matrix decomposition method (L+S) (20) for the Cartesian acquisition, one of the most popular methods due to its excellent reconstruction performance (16). Although these studies showed promising results using retrospectively undersampled data, no prospective undersampling reconstruction was shown.
Recently we developed an accelerated 2D T1ρ mapping method, which is referred to as SCOPE, and applied it for 2D T1ρ mapping of brain (21). A signal compensation strategy is applied in SCOPE to enhance the low rankness of the T1ρ-weighted image matrix and reconstruct images using the L+S method (20) followed by the inverse compensation. SCOPE needs to vectorize 2D images to construct the image matrix. The vectorization step leads to the loss of spatial information and may cause reconstruction degradation (22). When extending SCOPE to 3D T1ρ mapping, high-dimensional data can be treated as a tensor to avoid vectorizing the 3D images. This tensor-based representation has been successfully applied in dynamic MRI (22,23); it utilizes the spatial coherence of the image and, hence, can improve the reconstruction performance.
In this study, we investigated the feasibility of a signal-compensated robust tensor principal component analysis (TenSCOPE) method for accelerated 3D cartilage T1ρ mapping. In this framework, we decompose the 3D T1ρ-weighted images compensated at different TSLs as a low-rank high-order tensor plus sparse component. Both retrospective and prospective experiments were performed to assess the performance of TenSCOPE.
Methods
Robust tensor principal component analysis (RTPCA) model
The T1ρ-weighted image matrix can be decomposed as a superposition of a sparse component and a low-rank tensor ℒ. The corresponding optimization model is defined using the following formula:
where is the image series to be reconstructed and represents the acquired k-space data. N1, N2, and N3 represent the number of frequency- and phase-encoding lines in kx, ky, and kz, respectively. NTSL is the total number of TSLs, and Nc represents the channel number. denotes the sparse representation operator. represents the multicoil encoding operator which performs the multiplication with coil sensitivities followed by the undersampled Fourier transform (20,24). ℰ is the measurement error.
The rank of the tensor ℒ needs to be minimized. However, unlike matrix rank, the definition of tensor rank depends on the decomposition methods, which is not unique (25,26). Generally, a tensor can be decomposed as the sum of several rank-1 tensors. Tensor rank is based on the number of rank-1 tensors. We used Tucker decomposition in this work as a generalization of the matrix singular-value decomposition (SVD) in the high-dimensional space that is computationally tractable and flexible (27). Specifically, this process decomposes a tensor into the multiplication between a core tensor and matrices along each mode, which is similar to the SVD of matrices, as shown in Figure 1A. A demonstration of Tucker decomposition is shown in Algorithm 1. The rank of the tensor in mode i of unfolding is defined as:
where ℒi represents the mode-i matricization of tensor ℒ, which can be defined as ℒi=unfold(ℒ,i) (26). The i-rank can be regarded as a generalization of the SVD rank (for a matrix, these two are equivalent). With this definition, a low rank tensor is a tensor with all low rank unfoldings. Therefore, to estimate low-rank tensors, the multi-dimensional tensor trace norm of an i-order tensor is calculated using the weighted sum of the nuclear norms of the unfoldings in each mode:
where λ = [λ1,λ2,…,λn]T represents the rank regularization parameters of different unfolding matrices for the Tucker nuclear norm. With the above tensor rank definition, Eq. [1] can be reformed as:
TenSCOPE model
In TenSCOPE, a signal compensation strategy is applied by multiplying the T1ρ-weighted image signal by the compensation coefficient. The compensation coefficient can be calculated via the inversion of the T1ρ decay using the following formula:
where TSLk represents the spin-lock duration for the kth T1ρ-weighted image, and NTSL is the total TSL number. The compensated T1ρ-weighted images are then obtained with the RTPCA model. The optimization model of the TenSCOPE method is defined as follows:
where C(∙) denotes the pixelwise signal compensation operator using the above compensation coefficients Coefk (21). The signal intensity of the image matrix in the TSL direction should be the same after applying the signal compensation, and the rank of ℒ will then decrease.
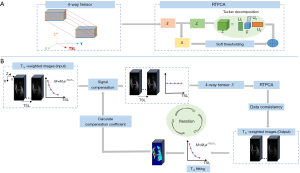
The solution strategy for Eq. [6] is summarized in Algorithm 2 and depicted in Figure 1B. First, the T1ρ-weighted image series to be reconstructed is involved in signal compensation. Low-resolution T1ρ maps are reconstructed using the fully sampled k-space center to estimate the initial compensation coefficient. Specifically, the compensation was performed by multiplying the original image signal by the inversion of the monoexponential decay at each voxel. Then, the image series represented by a 4-way tensor were decomposed by a low-rank tensor ℒ and a sparse component . ℒ and were obtained using Tucker decomposition [denoted by (∙)] and soft thresholding [denoted by (∙)], respectively, to reconstruct the T1ρ-weighted images. Soft thresholding is defined as follows:
where unfold(,i) represents the mode-i matricization of tensor ; fold(·) represents the inverse process, which folds a matrix to a tensor; p is an element of the image matrix; v represents the threshold. In the j-th iteration, the data consistency is enforced by ℒj+j−C(*(C−1(ℒj+j)−)), where C−1(·) represents the division of the image signal by the compensation coefficient in Eq. [5] pixel by pixel. * is the adjoint operation of , which performs the backward function (21,24). The reconstructed T1ρ-weighted images are then used to update the T1ρ maps with the exponential model, and are applied to update the compensation coefficient. The image reconstruction and compensation coefficient updating steps are repeated alternately until the algorithm convergence is reached. The stopping criterion in this method is defined as the point when the algorithm reaches the maximum number of iterations or at which the relative change in the solutions in two consecutive iterations is less than a predefined value.
T1ρ map estimation
T1ρ maps are obtained by fitting the reconstructed T1ρ-weighted images with different TSLs pixel by pixel:
where M0 is the baseline image intensity without applying a spin-lock pulse and Mk is the signal intensity for the kth TSL image. During reconstruction, a log-based linear fitting method was used to update the T1ρ map and reduce the calculation complexity (21). The final T1ρ map was estimated using the nonlinear least-squares fitting method with the Levenberg-Marquardt algorithm from the reconstructed T1ρ-weighted images.
Data acquisition and reconstruction
All the MR scans were performed on a 3T scanner (uMR 790, United Imaging Healthcare, Shanghai, China) using a commercial 12-channel phased-array knee coil. T1ρ-weighted image datasets of the knee were acquired using a 3D modulated flip angle technique in refocused imaging with an extended echo train (MATRIX) sequence and a self-compensated paired spin-lock preparation pulse (28). The spin-lock frequency was fixed at 500 Hz (B1 of spin-lock pulse =11.74 µT). Three healthy volunteers (1 male, age: 26 years old; 2 females, age: 45±15 years old) were recruited for T1ρ scanning. The imaging parameters were: TE/TR =8.96/2,000 ms, matrix size: 256×146×124, pixel size = 0.98×0.98×1 mm3, echo train length =60,echo spacing =4.48 ms, and TSLs =5, 10, 20, 40, and 60 ms. The scan time for the fully sampled dataset with elliptical scanning was 39 minutes and 30 seconds. The fully sampled k-space datasets were retrospectively undersampled using Poisson-disk random (15,18) patterns with R=5.2, 7.7, and 9.7. The sampling masks for each TSL are different. Figures 2 and 3 show the applied undersampling pattern of ky-kz for R=5.2 and R=9.7. Data were fully sampled in the frequency encoding direction. To estimate the coil sensitivity map, the central k-space area was fully sampled with size =16×16 for R=5.2 and R=7.7 and size =12×12 for R=9.7. Furthermore, the T1ρ mapping data were prospectively undersampled using the Poisson-disk randomly undersampled scheme with net acceleration factors R=5 and R=7. Two volunteers (one male, 29 years old; one female, 30 years old) were involved in the prospectively study. The imaging parameters were the same as those used in the retrospective experiment. The scan time was 10 minutes and 10 seconds for R=5 and 7 minutes and 20 seconds for R=7. Due to the time limit, the reference scan was acquired using the PI with accelerating factor R=3. The reference images were then reconstructed using the ESPIRIT method (29) from the BART toolbox (download link: https://people.eecs.berkeley.edu/~mlustig/Software.html). The scan time for the reference scan was 18 minutes and 50 seconds.
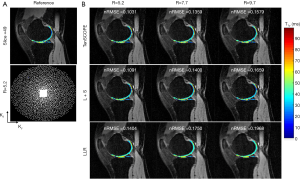
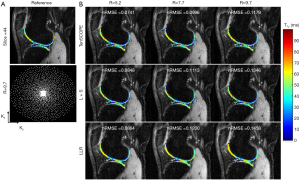
The TenSCOPE method was applied to reconstruct the 3D T1ρ-weighted image series. In the retrospective reconstruction, the iteration numbers of the outer loop were 4, 5, and 6 for R=5.2, 7.7, and 9.7 respectively. For the inner loop, the corresponding iteration numbers were 16, 18, and 20. In the prospective reconstruction, the iteration numbers for R=5 and 7 were 4 and 5 for the outer loop and 16 and 20 for the inner loop, respectively. All the tensor transforms and decompositions were implemented using the MATLAB tensor toolbox by Brett et al. from Sandia National Laboratories (download link: http://www.tensortoolbox.org/). In this study, 4 parameters needed to be tuned in the Tucker decomposition, and the reconstruction quality depends on 3 rank constraint parameters that control the complexity of spatial redundancy and 1 rank constraint parameter that controls the complexity of temporal redundancy in Tucker decomposition. The spatial redundancy parameters are chosen empirically as 0.45× the number of frequency-encoding lines, 0.65× the number of phase-encoding lines, and 0.65× the number of partition-encoding lines (30). Since signal compensation enhances the low rankness of the image matrix in the parameter direction, the temporal redundancy parameter is set as 1. The threshold in soft thresholding for different TSLs was set as [0.02, 0.02, 0.025, 0.025, 0.03]. For comparison, the L+S method (20) and the locally low-rank method (LLR) (31) were also applied to reconstruct the undersampled k-space data. In the L+S method, the singular-value thresholding and soft-thresholding algorithms (20) were used to solve for the L component and S component, respectively. The ratio for singular-value thresholding was set as 0.02, and the ratio for soft thresholding was set as [0.02, 0.025, 0.025, 0.035, 0.035] to achieve optimal performance. In the LLR method, the iteration number was set as 40, 50, and 60 for R=5.2, 7.7, and 9.7, respectively. The block size was set as 8×8, and the threshold for the singular value decomposition was initially set as 0.03 of the largest singular value, reduced to 0.01 after 10 iterations, and finally reduced to 0.005 in the final 10 iterations.
Assessment
The quality of the reconstructed T1ρ-weighted images was assessed based on the normalized root mean square error (nRMSE) using the following formula:
where xest is the reconstructed image from the undersampled k-space data, xref denotes the reference image from the fully sampled data.
The T1ρ quantification was assessed using the median of the normalized absolute deviation (MNAD) (16) and the mean T1ρ values (18) from the accelerated reconstruction for all the pixels in the selected cartilage regions of interest (ROIs) from all the acquisitions. In addition, three ROIs in the cartilage region were manually selected from four slices of each dataset (a total of 36 ROIs), and the mean T1ρ values were calculated for each ROI. Cartilage was segmented manually according to Li et al.’s work (12). Linear regression and Bland-Altman analysis were used to assess the agreement of the T1ρ parameter between the accelerated reconstructions and the reference.
The MNAD was defined as:
where pref(m) represents the reference parameter from fully sampled data; p(m) represents the T1ρ parameter estimated from the reconstructed images of the undersampled data. An MNAD of 0.1 corresponds to a median deviation of 10% from the estimated parameters compared with the reference.
The mean T1ρ value of the selected ROI compartment was defined as follows:
where N represents the number of pixels in the selected ROI compartment, represents the mean value of the selected ROI compartment, and represents the value of the nth pixel of the selected ROI compartment.
In the prospective experiments, the T1ρ values of the selected ROIs in cartilage regions from the 2 subjects were also calculated and then compared with the reference values by the Wilcoxon signed-rank test. Statistical significance was set to P<0.05.
All the image reconstructions and analyses were performed in MATLAB 2017b (The MathWorks, Natick, MA, USA) on an HP workstation with 160 GB DDR4 RAM and 32 cores (two 16-core Intel Xeon E5-2660 2.6 GHz processors).
The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013). The study was approved by the Ethics Committee at the Shenzhen Institute of Advanced Technology, Chinese Academy of Sciences (Ethics Committee approval number: SIAT-IRB-200315-H0455), and written informed consent was obtained from all patients.
Results
The T1ρ-weighted images (at TSL =5 ms) from two volunteers using the TenSCOPE, L+S and LLR methods are shown in Figures 2 and 3. The estimated T1ρ maps in selected ROIs are overlaid on the reconstructed images. The T1ρ-weighted images reconstructed using the LLR method are more blurred than those using the other two methods, showing obvious smoothing artifacts. By adding the sparse component to the low-rank-based method, i.e., using the L+S method, the smoothing artifacts are alleviated. The T1ρ-weighted images reconstructed using the TenSCOPE method show comparable image quality to the reference and achieve lower nRMSEs than images reconstructed using the L+S method for all acceleration factors. The T1ρ maps estimated from the TenSCOPE reconstructions show good agreement with the reference estimated from the fully sampled acquisition. Figure 4 shows the nRMSEs and MNADs of the selected ROIs (shown in Figure 5) from the accelerated reconstructions of the two datasets. The TenSCOPE reconstructions are more accurate than those obtained using the L+S and LLR methods, with the lowest nRMSE and MNAD values obtained for all acceleration factors. TenSCOPE improves the quality of the T1ρ maps in terms of the MNAD relative to that of the L+S method, especially for high-acceleration cases.
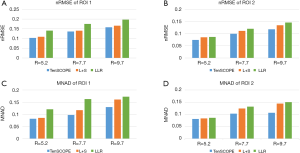
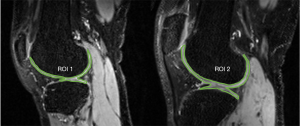
Figure 6 shows the scatter plots and Bland-Altman plots of the mean T1ρ values of ROIs using TenSCOPE compared with a reference. In the linear regression analyses, the estimated T1ρ values using TenSCOPE show good agreement with the reference (R2=0.9554 for 5.2× acceleration, R2=0.9213 for 7.7× acceleration, and R2=0.9209 for 9.7× acceleration). In the Bland-Altman analyses, the T1ρ values agree well with the reference values for R=5.2 (T1ρ: mean ± std: 40.4±1.4 ms, bias: 0.3 ms, 95% CI: −2.5, 3.1), R=7.7 (T1ρ: mean ± std: 40.4± 2.1 ms, bias: 1.5 ms, 95% CI: −2.6, 5.6), and R=9.7 (T1ρ: mean ± std: 40.9±2.2 ms, bias: 1.5 ms, 95% CI: −3.0, 5.9). No statistically significant differences were observed between the T1ρ values measured across the subjects with different acceleration factors and the fully sampled reference.

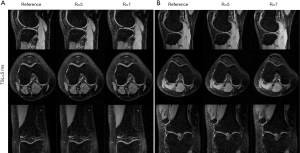
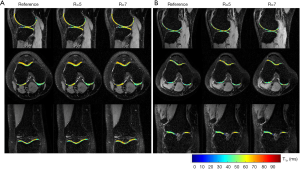
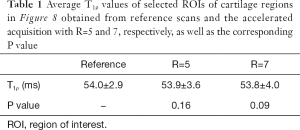
Figure 7 shows the T1ρ-weighted images obtained from the prospectively undersampled data using the TenSCOPE method for R=5 and R=7. Reference images are also shown for comparison. Figure 8 shows the corresponding T1ρ parameter maps estimated from the reconstructed images. The T1ρ maps in the selected ROIs of cartilage regions were overlaid on the reconstructed T1ρ-weighted images at TSL =5 ms. No obvious blurring artifacts were observed in the T1ρ-weighted images and T1ρ maps reconstructed using the TenSCOPE method for R=5 and R=7. The results of T1ρ values of the selected ROIs in cartilage regions shown in Figure 8 and the Wilcoxon signed-rank test are shown in Table 1. There were no statistically significant differences between the T1ρ values measured by TenSCOPE for either accelerated scans (R=5, 7) or the reference values for the selected ROIs (both P>0.05).
Full table
Discussion
In this work, we developed a novel accelerated 3D T1ρ mapping of knee cartilage method to obtain the T1ρ parameters from highly undersampled data with the acceleration factor up to 9.7. The signal-compensated robust tensor principal component analysis model for image reconstruction displayed excellent performance. According to our results, the reconstructed T1ρ-weighted images using TenSCOPE showed fewer blurring artifacts and achieved lower reconstruction errors than those obtained with other methods, i.e., the LLR method. Even at a high acceleration factor, the TenSCOPE method still maintains reasonable image quality and accurate T1ρ maps. The resulting T1ρ estimations show good agreement with the reference derived from the fully sampled data.
CS has been successful for accelerating T1ρ mapping of knee cartilage. In Pandit et al. (14), a method which combined CS and autocalibrating reconstruction for Cartesian sampling (ARC) was applied to accelerate T1ρ mapping of knee cartilage with acceleration factors up to 2.3. T1ρ maps obtained from the retrospective reconstructions using this method were shown with errors less than 5%. In Zhou et al. (18), a combined reconstruction with locally adaptive iterative support detection (k-t LAISD) and PI was used to accelerate T1ρ mapping of knee cartilage. The T1ρ quantification results showed high fidelity between accelerated and fully sampled data with achieved acceleration factors of 3 and 3.5, due to the local adaptability of the regularization and joint estimation of the coil sensitivities. In the above two studies, no prospective undersampling was implemented and the sparse prior was mainly used. In Zibetti et al. (16), CS reconstruction using 12 different sparsifying transforms was compared in reducing the scan time of T1ρ mapping for cartilage, and the low rank with spatial finite difference (L+S SFD) transform is suggested as one of the most suitable sparsifying transforms. In this work, we combined low-rank and sparse priors in the CS reconstruction and applied a signal-compensated robust tensor principal component analysis model to reconstruct 3D images from undersampled data. We provide comparable or better results compared with state-of-the-art CS methods. The prospective reconstructions showed that the proposed TenSCOPE method can achieve comparable performance to the reference scan using PI.
In our previous work (21), we showed that obvious blur artifacts were observed in the reconstructions using the low-rank-based methods such as LLR. By adding the sparse component to the low-rank method, the smoothing artifacts were alleviated. The same conclusion can be drawn from Figures 2 and 3. Similar to the SCOPE method in our previous work, the sparse component in the proposed TenSCOPE method is the differentiation between the acquired images and the exponential relaxation model resulting from hardware imperfections of the MR scanner, noise, and other factors. The strength of the differentiation varies according to TSL, and it may be better to use different thresholds for the images at different TSLs. In previous studies (20,32), L+S decomposition was applied to dynamic imaging or multispectral imaging, in which the data did not fit a low-rank only component and therefore the sparse component contains significant energy. L+S decomposition was applied in static imaging in this study, but we found that some image details can still be observed in the sparse component, especially in the cartilage region. Therefore, although the energy (about 4.31% in average for our knee data) in the sparse component was relatively small, it could not be neglected in the reconstruction.
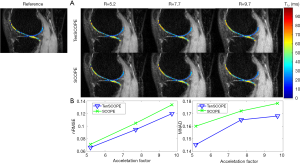
In our recent work (33), we applied the SCOPE method to reconstruct the T1ρ-weighted images slice-by-slice in a 2D reconstruction version and showed the superiority of this method over the L+S method. In this study, we used a low-rank tensor to replace the low-rank matrix to capture the data correlation in multiple dimensions beyond the TSL direction. To validate the effectiveness of tensors in the reconstruction, we also compared TenSCOPE with SCOPE. Figure 9 shows the reconstruction results using the proposed TenSCOPE and SCOPE methods. It can be observed that TenSCOPE improves the quality of the T1ρ-weighthed images and T1ρ maps in terms of the nRMSE and MNAD relative to that of the SCOPE method, with lower nRMSEs and MNADs than SCOPE for all the acceleration factors.
In the proposed TenSCOPE method, the initial signal compensation coefficient was calculated from the center of fully sampled k-space data. The performance may be improved by adding a pre-reconstruction step; notably, the missing k-space data are interpolated using a TV-regularized estimate (34) prior to estimating the initial signal compensation coefficient. However, no such pre-reconstruction is necessary for the proposed method since the coefficient is updated iteratively in the reconstruction step. Four parameters, including the outer iteration number, inner iteration number, rank parameter for Tucker decomposition, and threshold for the sparse component, need to be carefully selected in the optimization process. All the iteration numbers and the thresholds for the sparse component were selected empirically.
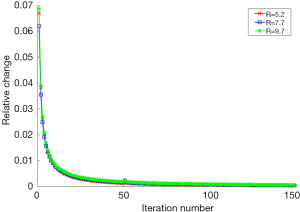
To evaluate the convergence of the proposed method, we calculated the relative change of image norm between two consecutive iterations at different undersampling levels with R=5.2, R=7.7 and R=9.7. The relative change was defined as
where Iiter represents the reconstructed image in the iter-th iteration. The iteration number includes both the inner and outer iterations. Figure 10 shows the relative change for the reconstructed image during each iteration. It demonstrates that the proposed algorithm converges with different undersampling levels as long as the iteration number is large enough. In this work, the algorithm iterates until the algorithm reaches the maximum number of iterations or the relative change in the solution is less than 5×10−4.
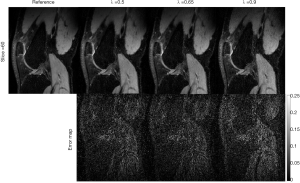
The rank parameter for Tucker decomposition is an important parameter in the TenSCOPE method. Figure 11 shows an example of the reconstructed T1ρ-weighted images with different rank parameters used in the Tucker decomposition at TSL =5 ms for one slice of the dataset with R=7.7. While an insufficient tensor rank may lead to blurring artifacts or bias the T1ρ measurements, high values can lead to limited noise reduction. Furthermore, the rank needs to be prespecified before running TenSCOPE. In this study, the rank parameter was selected empirically (30). An optimized rank parameter may help improve reconstruction performance (35). Regarding the regularization parameter for the sparse component, there is a trade-off between the convergence speed and the image quality. The algorithm converges more slowly using a small parameter, and more image details will be lost if a larger parameter is used, while the noise will not be sufficiently removed using a smaller parameter (Figure 12).
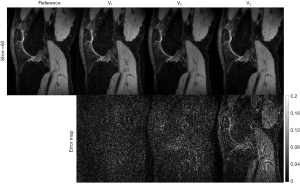
Since the T1ρ map was updated in each outer iteration, Tucker decomposition was performed in each iteration, which further increased the computational burden of the proposed method. In our current implementation, the computation was approximately 3 hours for each iteration for a data set size of 256 (frequency encoding) ×146 (phase encoding) ×124 (slices) ×12 (channel) ×5 (TSL). To reduce the reconstruction time, we applied parallel computing in MATLAB in the process of the T1ρ map estimation. The number of workers used in parallel computing is 30, and the reconstruction times for R=5.2, 7.7, and 9.7 were 4.7, 6.8 and 8.5 hours, respectively. The reconstruction time of the TenSCOPE was longer than that of the L+S method and comparable to that of the LLR method. Taking R=5 as an example, the times required for L+S and LLR were 4.3 and 4.75 hours, respectively. The computational speed can be further improved by using a C implementation or graphical processing units (GPUs) instead of MATLAB.
PI can be integrated with CS-based methods to further accelerate the acquisition. In most CS-based fast MR parameter mapping methods, the fully sampled k-space center prolongs the acquisition time since multiple T1ρ-weighted images need to be acquired, especially in 3D T1ρ mapping applications. Therefore, PI can be used to undersample the k-space center to further reduce the acquisition time (36). For reconstruction, the undersampled k-space center can be first reconstructed with Generalized Autocalibrating Partial Parallel Acquisition (GRAPPA), and the proposed TenSCOPE method can then be used to reconstruct the T1ρ-weighted images.
This work lacks longitudinal reproducibility and variations in cartilage T1ρ studies. The longitudinal reproducibility and variations in cartilage T1ρ are necessary in studies with clinical applications, such as cartilage degeneration evaluations. In future studies, longitudinal reproducibility assessments will be performed for clinical studies by applying the TenSCOPE method to detect early cartilage damage and degeneration in patients with OA, acute joint injury or cartilage damage.
Conclusions
We introduced a TenSCOPE method that uses a signal-compensated robust tensor principal component analysis model to reconstruct 3D images from undersampled data. The proposed method yields reasonable parameter estimates at high acceleration factors for the 3D T1ρ mapping of in vivo knee cartilage, thereby reducing the scan time.
Acknowledgments
Funding: This work was partially supported by the National Key R&D Program of China Nos. 2020YFA0712200, 2017YFC0108802, National Natural Science Foundation of China under grant Nos. 61771463, 81830056, U1805261, 61671441 and 81971611, the Innovation and Technology Commission of the government of Hong Kong SAR under grant no. MRP/001/18X, the Key Laboratory for Magnetic Resonance and Multimodality Imaging of Guangdong Province under grant No. 2020B1212060051, and by the Chinese Academy of Sciences program under grant No. 2020GZL006.
Footnote
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at http://dx.doi.org/10.21037/qims-20-790). DL serves as an unpaid Editorial Board Member of Quantitative Imaging in Medicine and Surgery. The other authors have no conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013). The study was approved by the Ethics Committee at the Shenzhen Institute of Advanced Technology, Chinese Academy of Sciences (Ethics Committee approval number: SIAT-IRB-200315-H0455), and written informed consent was obtained from all patients.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Jinks C, Jordan K, Croft P. Osteoarthritis as a public health problem: the impact of developing knee pain on physical function in adults living in the community: (KNEST 3). Rheumatology 2007;46:877-81. [Crossref] [PubMed]
- Matzat SJ, van Tiel J, Gold GE, Oei EH. Quantitative MRI techniques of cartilage composition. Quant Imaging Med Surg 2013;3:162-74. [PubMed]
- Baboli R, Sharafi A, Chang G, Regatte RR. Isotropic morphometry and multicomponent T1 rho mapping of human knee articular cartilage in vivo at 3T. J Magn Reson Imaging 2018;48:1707-16. [Crossref] [PubMed]
- Koster IM, Oei EH, Hensen JH, Boks SS, Koes BW, Vroegindeweij D, Hunink MG, Bierma-Zeinstra SM. Predictive factors for new onset or progression of knee osteoarthritis one year after trauma: MRI follow-up in general practice. Eur Radiol 2011;21:1509-16. [Crossref] [PubMed]
- Glyn-Jones S, Palmer AJ, Agricola R, Price AJ, Vincent TL, Weinans H, Carr AJ. Osteoarthritis. Lancet 2015;386:376-87. [PubMed]
- Baum T, Joseph GB, Karampinos DC, Jungmann PM, Link TM, Bauer JS. Cartilage and meniscal T2 relaxation time as non-invasive biomarker for knee osteoarthritis and cartilage repair procedures. Osteoarthritis Cartilage 2013;21:1474-84. [Crossref] [PubMed]
- Mosher TJ, Zhang Z, Reddy R, Boudhar S, Milestone BN, Morrison WB, Kwoh CK, Eckstein F, Witschey WR, Borthakur A. Knee articular cartilage damage in osteoarthritis: analysis of MR image biomarker reproducibility in ACRIN-PA 4001 multicenter trial. Radiology 2011;258:832-42. [Crossref] [PubMed]
- Li X, Han ET, Ma CB, Link TM, Newitt DC, Majumdar S. In vivo 3T spiral imaging based multi-slice T(1rho) mapping of knee cartilage in osteoarthritis. Magn Reson Med 2005;54:929-36. [Crossref] [PubMed]
- Wáng YX, Zhang Q, Li X, Chen W, Ahuja A, Yuan J. T1ρ magnetic resonance: basic physics principles and applications in knee and intervertebral disc imaging. Quant Imaging Med Surg 2015;5:858-85. [PubMed]
- Li X, Majumdar S. Quantitative MRI of articular cartilage and its clinical applications. J Magn Reson Imaging 2013;38:991-1008. [Crossref] [PubMed]
- Bolbos RI, Zuo J, Banerjee S, Link TM, Ma CB, Li XJ, Majumdar S. Relationship between trabecular bone structure and articular cartilage morphology and relaxation times in early OA of the knee joint using parallel MRI at 3 T. Osteoarthritis Cartilage 2008;16:1150-9. [Crossref] [PubMed]
- Li X, Benjamin Ma C, Link TM, Castillo DD, Blumenkrantz G, Lozano J, Carballido-Gamio J, Ries M, Majumdar S. In vivo T(1rho) and T(2) mapping of articular cartilage in osteoarthritis of the knee using 3 T MRI. Osteoarthritis Cartilage 2007;15:789-97. [Crossref] [PubMed]
- Stahl R, Luke A, Li XJ, Carballido-Gamio J, Ma CB, Majumdar S, Link TM. T1rho, T2 and focal knee cartilage abnormalities in physically active and sedentary healthy subjects versus early OA patients--a 3.0-Tesla MRI study. Eur Radiol 2009;19:132-43. [Crossref] [PubMed]
- Pandit P, Rivoire J, King K, Li X. Accelerated T1ρ acquisition for knee cartilage quantification using compressed sensing and data-driven parallel imaging: A feasibility study. Magn Reson Med 2016;75:1256-61. [Crossref] [PubMed]
- Zibetti MVW, Baboli R, Chang G, Otazo R, Regatte RR. Rapid compositional mapping of knee cartilage with compressed sensing MRI. J Magn Reson Imaging 2018;48:1185-98. [Crossref] [PubMed]
- Zibetti MVW, Sharafi A, Otazo R, Regatte RR. Accelerating 3D-T 1ρ mapping of cartilage using compressed sensing with different sparse and low rank models. Magn Reson Med 2018;80:1475-91. [Crossref] [PubMed]
- Zibetti MVW, Sharafi A, Otazo R, Regatte RR. Compressed sensing acceleration of biexponential 3D-T 1ρ relaxation mapping of knee cartilage. Magn Reson Med 2019;81:863-80. [Crossref] [PubMed]
- Zhou Y, Pandit P, Pedoia V, Rivoire J, Wang Y, Liang D, Li X, Ying L. Accelerating T1ρ cartilage imaging using compressed sensing with iterative locally adapted support detection and JSENSE. Magn Reson Med 2016;75:1617-29. [Crossref] [PubMed]
- Zibetti MVW, Sharafi A, Otazo R, Regatte RR. Accelerated mono- and biexponential 3D-T1ρ relaxation mapping of knee cartilage using golden angle radial acquisitions and compressed sensing. Magn Reson Med 2020;83:1291-309. [Crossref] [PubMed]
- Otazo R, Candes E, Sodickson DK. Low-Rank Plus Sparse Matrix Decomposition for Accelerated Dynamic MRI with Separation of Background and Dynamic Components. Magn Reson Med 2015;73:1125-36. [Crossref] [PubMed]
- Zhu Y, Liu Y, Ying L, Peng X, Wang YJ, Yuan J, Liu X, Liang D. SCOPE: signal compensation for low-rank plus sparse matrix decomposition for fast parameter mapping. Phys Med Biol 2018;63:185009 [Crossref] [PubMed]
- Roohi SF, Zonoobi D, Kassim AA, Jaremko JL. Multi-dimensional low rank plus sparse decomposition for reconstruction of under-sampled dynamic MRI. Pattern Recognition 2017;63:667-79. [Crossref]
- Liu Y, Liu T, Liu J, Zhu C. Smooth robust tensor principal component analysis for compressed sensing of dynamic MRI. Pattern Recognition 2020;102:107252 [Crossref]
- Pruessmann KP, Weiger M, Bornert P, Boesiger P. Advances in sensitivity encoding with arbitrary k-space trajectories. Magn Reson Med 2001;46:638-51. [Crossref] [PubMed]
- De Lathauwer L, De Moor B, Vandewalle J. On the best rank-1 and rank-(R1, R2,RN) approximation of higher-order tensor. SIAM Journal on Matrix Analysis and Applications 2000;21:1324-42. [Crossref]
- Ying JX, Lu HF, Wei QT, Cai JF, Guo D, Wu JH, Chen Z, Qu XB. Hankel Matrix Nuclear Norm Regularized Tensor Completion for N-dimensional Exponential Signals. IEEE Trans Signal Process 2017;65:3702-17. [Crossref]
- Long Z, Liu YP, Chen LX, Zhu C. Low rank tensor completion for multiway visual data. Signal Processing 2019;155:301-16. [Crossref]
- Mitrea BG, Krafft AJ, Song R, Loeffler RB, Hillenbrand CM. Paired self-compensated spin-lock preparation for improved T1ρ quantification. J Magn Reson 2016;268:49-57. [Crossref] [PubMed]
- Uecker M, Lai P, Murphy MJ, Virtue P, Elad M, Pauly JM, Vasanawala SS, Lustig M. ESPIRiT--an eigenvalue approach to autocalibrating parallel MRI: where SENSE meets GRAPPA. Magn Reson Med 2014;71:990-1001. [Crossref] [PubMed]
- Cao W, Wang Y, Sun J, Meng D, Yang C, Cichocki A, Xu Z. Total Variation Regularized Tensor RPCA for Background Subtraction From Compressive Measurements. IEEE Trans Image Process 2016;25:4075-90. [Crossref] [PubMed]
- Zhang T, Pauly JM, Levesque IR. Accelerating parameter mapping with a locally low rank constraint. Magn Reson Med 2015;73:655-61. [Crossref] [PubMed]
- Levine E, Stevens K, Beaulieu C, Hargreaves B. Accelerated three-dimensional multispectral MRI with robust principal component analysis for separation of on- and off-resonance signals. Magn Reson Med 2018;79:1495-505. [Crossref] [PubMed]
- Liu Y,Chen W, Liu X, Zheng H,Liang D, Zhu Y. Accelerating 3D-T1ρ Cartilage imaing using signal compensated low-rank plus sparse matrix decomposition. In Proceedings of the 28th Annual Meeting of ISMRM, Virtual Conference, 2020. Abstract 2744.
- Yang JF, Zhang Y, Yin WT. A Fast Alternating Direction Method for TVL1-L2 Signal Reconstruction From Partial Fourier Data. IEEE Journal of Selected Topics in Signal Processing 2010;4:288-97. [Crossref]
- Yaman B, Weingartner S, Kargas N, Sidiropoulos ND, Akcakaya M. Low-Rank Tensor Models for Improved Multi-Dimensional MRI: Application to Dynamic Cardiac T 1 Mapping. IEEE Trans Comput Imaging 2019;6:194-207. [Crossref] [PubMed]
- Zhu Y, Liu Y, Ying L, Qiu Z, Liu Q, Jia S, Wang H, Peng X, Liu X, Zheng H, Liang D. A 4-minute solution for submillimeter whole-brain T 1ρ quantification. Magn Reson Med 2021;85:3299-307. [Crossref] [PubMed]




