
Robust three-dimensional registration on optical coherence tomography angiography for speckle reduction and visualization
Introduction
Optical coherence tomography (OCT) is a non-invasive and three-dimensional (3D) biomedical imaging technique that can provide cross-sectional images of a tissue sample with micrometer level resolution (1,2). OCT has been proven clinically useful in ophthalmology and is gradually becoming the gold standard for the diagnosis of many retinal diseases (1-4). Recently, OCT angiography (OCTA) has emerged as a novel non-invasive tool that can visualize functional blood vessels down to capillary levels in clinical settings (5-7). The capabilities of OCT and OCTA have made revolutionary impact on how ophthalmologists understand ocular disease pathologies as well as manage the therapeutic treatments. In addition to the rapid translation of OCTA into clinical ophthalmology, it has also been shown increasing promises in the fields of dermatology (8), otolaryngology (9), dentistry (10) and cardiology (11).
Despite their increasing popularity, OCT and OCTA still face several challenges in terms of the image quality for the purposes of providing more accurate quantification information. The motion artifacts and the inherent speckle noise from imaging process would significantly compromise its image quality, thus affect the accuracy and repeatability of microvasculature quantification (12,13). Previous method has suggested that multiple-volume or repeat B-scan averaging strategy can compensate motion artifacts and reduce speckle noises (5,14,15). This method requires spatial alignment of the repeated scans or volumes before performing averaging. In practice, subjects are often in motion, albeit small, during scanning. The motion, including but not limited to the respiration and heartbeat that are not inevitable, would introduce misalignment in the OCT raster scans during the process of averaging. Specifically, in dermatological OCT imaging, the inter-frame motion artifacts and global movement would corrupt the alignment of the repeated successively acquired volumes. Thus, add the difficulties to perform multi-volume averaging to enhance the image quality and clarity for the purpose of quantification. Also, in ocular imaging, eye motions, such as a slow shift in gaze (drift), high frequency involuntary motions (tremor), or rapid eye movement (saccades), can all lead to disconnected vessels and introduce stripes of motion artifacts, affecting our ability to provide quantitative measures of retinal vascular complex.
Therefore, the key to a successful averaging algorithm is the accurate spatial registration and alignment. Several methods have been proposed for 3D registration in OCT or OCTA for specially-designed system configurations (16) using post-processing algorithms (17). Tracking and compensation strategies have also been proposed and utilized to mitigate the subject motion artifacts, such as with an aid of scanning laser ophthalmoscopy (18) and using wavefront sensors (19). However, these prior approaches usually either require expensive and sophisticated system setup, or increase the total acquisition time that inevitably reduces patient compliance. Other than the hardware approaches mentioned above, software processing algorithms can also be used to reduce speckle noise and motion artifacts. Generally, one can register multiple repeated OCT volumes to mitigate the above mentioned issues and enhance the signal to noise ratio (SNR). Ideally, the OCT signals sampled at the same spatial location with sufficient time interval are correlated. As a result, the averaged signal of repeatedly sampled signals improves the SNR by suppressing the random fluctuating noise while maintaining the true signals (20). Potsaid et al. (21) proposed a method of two dimensional (2D) registration on cross-sectional images to correct the volumetric motion, but it is computationally cost on 3D images. In addition, this method was only designed for correcting motion between slow scans. Kraus et al. (22) introduced a method with orthogonal scanning pattern that uses intensity based registration to minimize the motion artifacts in the OCT system. This method combines the information of fast and slow scans to register and acquire the artifact-free images. Although it has been adopted in commercial OCT systems (e.g., Optovue SD-OCTA machine), it still suffers from residual inter-frame artifact when large inter-volume mismatch exists. The requirement of a special scanning pattern for this algorithm also increases the difficulties for it to be adapted by other commercial OCT systems.
Moreover, layer segmentation (23-26) or feature extraction approaches (27) have also been presented to guide the volumetric registration, such methods can correct global displacement of each sub-image or align the image based on the layer contour before co-registration. However, the robustness of such algorithms may decrease when the pathological cases are dealt with, and they tend to induce unpredictable registration errors. Therefore, there is still a demand to develop a registration and averaging method that can perform universal 3D registration on repeated OCT volumes using reasonable computation resources, without a need to modify the hardware configurations of current commercial OCT systems.
In this study, we propose a robust and comprehensive approach to register 3D OCT and OCTA volumes for speckle noise reduction, where successive OCT volumes are used to obtain the affine and B-spline transformations, upon which to obtain the coordinates of OCTA volumes for later co-registration and averaging. We demonstrate that this method can significantly increase the SNR of images and suppress motion induced artifacts, through testing the algorithm on the datasets acquired from human retina and human skin in vivo.
Methods
The workflow of 3D registration and averaging
In the registration model below, the images that are acquired when the sample is in motion are defined as IM and the fixed image that acts as the reference is referred to as IF. For any pixel located at x, the spatial transformation matrix T that aligns IF to IM is defined as:
[1]
where u(x) is the amount of motion, or the displacement due to global or local motion between coordinates. Note that the spatial location can be of (x,y,z) coordinates in 3D, here we use x for simplicity. Generally speaking, the intensity-based registration is a convex optimization problem that can be represented by the equation below, to obtain the correct spatial transformation.
[2]
In Eq. [2], represents the optimized transformation under the cost function C, which measures the deformation between the reference and registered image. Thus, the goal of image registration is to search for the best parameters vector μ for the transformation Tµ from IF to IM with a minimum cost. The number of parameters in vector μ defined by the transformation matrix T. There are 12 parameters in vector μ for affine transformation and (Px × Py × Pz) × 3 parameters for B-spline transformation, where Px,Py, Pz are the number of pixels in each dimension divided by the designed grid, which is 16 pixels in this study.
The cost function C here is formed by the mutual information (MI) term with the penalty term, as:
[3]
where α, β are user-defined parameters, with empirically set as 1.0 and 0.1 respectively. P[μ;IM] is a penalty term to reduce overfitting and to constrain the transformation matrix Tµ, which is modified from the rigidity penalty method introduced by Staring et al. (28). MI is defined as below:
[4]
where p is the discrete joint probability, and pF and pM are the marginal discrete probabilities of the reference and moving images, obtained by summing p over moving images m and the reference image f, respectively. The joint probability p is estimated using B-spline Parzen window described by Thévenaz (29). The MI depends on fewer assumptions of data and can provide better stability for optimizations comparing L1, the Manhattan distance or L2, the Euclidean distance.
In the optimization of the parameters vector μ for the cost function, we employed a method called adaptive stochastic gradient descent (ASGD) method. This algorithm randomly shuffles the datasets to calculate the gradients, updating the parameters with less variance to produce a more stable convergence. It also requires fewer parameters to be set and tends to be more robust by its adaptive step size. Mathematically, the ASGD can be represented as:
[5]
where μk denotes the registration parameter vector for optimization, γ(tk) denotes the step size and gk denotes the gradient of the cost function at step k. The learning rate is defined by a monotone decreasing function γ (30) and controlled by the incremental variable tk. In the determination of tk, S represents the sigmoid function to normalize the inner products of the gradients of previous two steps (30). If the directions of the gradients gk, gk–1 are same, the positive inner product of gradients will result to a small tk+1 and a larger step size γ(tk+1). Eq. [5] illustrates that the ASGD method implements an adaptive step size mechanism through adjusting the independent variable tk of step size γ(tk). The optimization starts with zero initiation of μ0, and the images are further sampled for calculating the cost function. At next step, μ1 is updated according to Eq. [5]. Then the algorithm will update the µk iteratively until reaching the predefined step number, which was set as 250 in this study. To summarize, the ASGD method {Eq. [5]} was used to update the transformation vector µ and to minimize the cost function Eq. [3] until desired vector µ is found.
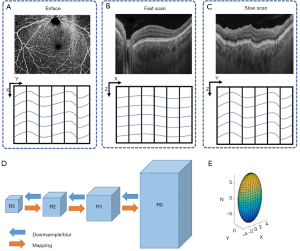
We utilized two approaches in our registration model. Firstly, we employed both affine and B-spline models to obtain the transformation matrix T. The affine transformation was designed to correct translation, scaling, shear, and rotation of the images, also known as global correction of relatively large movement (23,24). Afterward, we used the B-spline transformation to correct the free-form deformation, also known as irregular movement and local deformation correction (23,24) as shown in Figure 1. Secondly, we performed registration on different resolution levels iteratively in order to refine and minimize misalignments between 3D volume scans. Specifically, a range of Gaussian kernels were used to down sample OCT scans in a particular fashion to reduce the complexity and the amount of data. As illustrated in Figure 2, the original OCT scan R0 with highest resolution was down sampled to R1 and then further down sampled to R2, R3, and so on (31). The image size and resolution were decreased to form the image pyramids. The down sampling Gaussian kernel σ(x,y,z) was set with a size of [2,4,8] for the image pyramids and this was specifically designed to match the anisotropic motion patterns in OCT scans. In σ(x,y,z), z corresponds to the A-line direction, x corresponds to the B-scan direction (fast scan) and y corresponds to the C-scan direction (slow scan). The A-line acquisition speed is the fastest, with the least motion artifacts, and thus, down sampled the most (8 times). The C-scan acquisition speed is the slowest, with the highest probability to have motion artifacts, and consequently, down sampled the least (2 times). The down-sampling for the B-scan is in between. For each image pyramids, the registration process was first conducted on R3 as the optimization had better convergence on blurred images. Then the resulted parameters from R3 were applied and mapped back on R2-R0, as indicated by the orange arrows of Figure 2. Specifically, the affine transformation calculated by R3 was firstly applied onto R2 globally, then the B-spline transformation calculated by R3 on each grid was applied onto corresponding pixels on R2. The registration on R2 was then conducted on the modified images with less movements and its results were further applied to R1 and R0. The registration and mapping process were iteratively performed until R0 was reached.
After registration, the registered image was weighted and averaged with the reference image, which was then assigned as the new reference image for next round of registration as it has better contrast. The weighted averaging process for nth image is defined by the following rules, as shown in Figure 3.
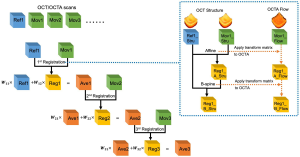
[6]
For nth registration, the designed weights ensure each individual image has the same weight 1⁄n in the final averaged results. We set the wn1=n/(n+1) as the weight for the reference image and the wn2=1/(n+1) as the weight for the registered image. IFix,n, IReg,n represent the corresponding reference image and registered image, respectively. In our study, all registrations were conducted on the OCT scans. Since OCT and OCTA datasets share the same spatial coordinates, transformations calculated from the OCT scans were stored and directly applied to OCTA scans as shown by the dash arrows of Figure 3. The implementation of the registration program was based on MATLAB (MathWorks, R2016a) and an open source project Elastix (32).
Data acquisition
Two datasets were collected to test the proposed algorithm: human skin data using a laboratory built SS-OCT 1,310 nm system (33) and human retina data acquired by a 1,050 nm swept-source OCT angiography (SS-OCTA) (PLEX® Elite 9000, Carl Zeiss Meditec, Dublin, CA, USA). Both systems have an imaging speed of 100 kHz. The subject imaging followed protocols reviewed and approved by the Institutional Review Board of Medical Sciences Subcommittee at the University of Washington, Seattle. The tenets of the Declaration of Helsinki and Health Insurance Portability and Accountability Act were followed. Informed consent forms were obtained from all subjects before participation.
For the human skin data acquired by the laboratory system, 10 consecutive OCT volumes with 9×9 mm scanning pattern were acquired from each subject. Each volume had a total of 2,400 B-scans with four repeated B-scans at each spatial B-location for the purpose of OCTA. Each B-scan had 600 A-scans. No tracking mechanism was employed in this system and the acquisition of 10 volumes took ~180 seconds for each subject in total. For the human retina data acquired by the commercial SS-OCTA device, 22 repeated 6×6 mm volume scans were acquired from the right eye of each subject. Of these 22 volume scans, 11 scans were acquired centered at the fovea and 11 scans were acquired ~9 mm inferonasally away from the fovea. Each scan takes about ~6 seconds and short breaks were taken between scans. The Fastrac motion tracking system was employed to minimize the eye motion during scanning, and the Track to Prior function was turned on to acquire repeated scans at the same location (34). For both sets of data, the ultrahigh sensitive optical microangiography (OMAG) (35) algorithm was used to generate OCTA volumes and the subpixel registration approach was applied to compensate the displacement between adjacent B-scans (36). After OCTA volumes were generated, the proposed registration algorithm was employed to register and average both OCT and OCTA data. After obtaining the average OCTA data, a semi-automatic segmentation software (37) was used to extract slabs of interest to demonstrate the quality of the resulting images. Human retina data were segmented into whole retina slab and choriocapillaris slab, following protocols of previously published study (38). Human skin data were segmented into different slabs for better visualization, following protocols of previously published study (8). After segmentation, the maximum intensity projection (MIP) was used to generate en face images.
Registration evaluation
To evaluate the performance of resulting registration and subsequent averaging, three parameters were used: peak signal-to-noise ratio (PSNR), normalized correlation coefficient (NCC), and SNR. The PSNR measures the quality of single scans compared with the high-quality averaged images. It is defined as:
[7]
where l,m,n represent the size of the volume, and I represents the intensity of data. The averaged high-quality image was picked as the reference image IH and the single scan image was denoted as image IS. MAXI is the maximum possible pixel value of the image. The whole 3D OCT volumes were used to quantify PSNR.
The NCC measures the similarity of images by assuming a linear relationship between the intensity values of the reference image and the moving image. It evaluates how well the volumes are aligned. The NCC is defined as:
[8]
The Tµ (x) represents the registered image IF that is suspected of motion.
The SNR is defined by the ratio of mean to standard deviation of the signal:
[9]
where μsignal is the mean of OCT signal and σnoise is the standard deviation of the background noise. The regions of tissues around the focus position were manually selected as the signal and the regions of no tissues were manually selected as noise floor. Theoretically, the mean of signals from individual samples improves linearly to the repetition N with the standard deviation inversely related to
Results
A total of five healthy subjects with a normal ocular history, no visual complains, and no identified optic disc, retinal, or choroidal pathologies on examination were recruited for human retina imaging and a total of five healthy volunteers were imaged for human skin imaging. To evaluate the performance of proposed algorithm, we examined the cost function at 4 resolution levels during the optimization, inspected visual appearance of the averaged images, and calculated quantitative metrics from averaged images describing image quality.
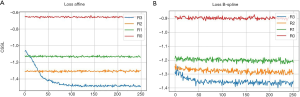
As explained in the Methods section, a cost function is commonly used to evaluate the differences of the reference (fixed) image and the image that is to be registered. This function indicates how well the registration algorithm performs. Figure 4 presents how the cost function changes with the number of iterations during optimizing the transformation parameters. Ideally, the value of the cost function should decrease with the increase of iterations and eventually reach a plateau, from where further increase of iteration would not benefit more the optimization. Figure 4A demonstrates how the cost function varies with the number of iterations for the affine transformation when the optimization was performed on 4 different resolution levels (R3-R0). The cost function decreases relatively fast on the low resolution level (R3), and reaches a plateau at about 100 iterations which would deliver similar performance to that of higher resolution levels (R0-R2). This means the optimal affine registration parameters can be obtained on the low resolution level images. Figure 4B demonstrates how the cost function changes for the B-spline transformation at different resolution levels (R3-R0). The cost decreases relative slowly, but still most significantly in the low resolution level (R3) images. However, unlike in the affine transformation, the value of the cost function is kept on decreasing at higher resolution level images (R1 and R2). That indicates the local movements are progressively aligned by the B-spline registration during the process. The parameter space for affine transformation is much smaller than the B-spline transformation, thus the cost function curves in Figure 4A converges for fewer iterations and on lower resolution level images than in Figure 4B. The appearance of cost function provides ground for selecting the number of iterations and the levels of down sampling during optimization. If the cost functions are converged on the lowest resolution level and keep same at higher levels (like Figure 4A), then the motion of images are not severe. The users can set less iterations and down sampling levels so that the optimization can speed up. Otherwise users can keep the default settings for better registration.
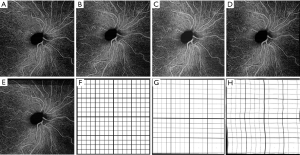
The averaged images suggest its effectiveness for noise reduction and contrast enhancement. Figure 5 shows an example of single (Figure 5A,C) and averaged (Figure 5B,D) OCT (Figure 5A,B) and OCTA (Figure 5C,D) B-scans. These B-scans were taken from 6×6 mm volumes centered at the fovea. Yellow dash lines indicate zoomed-in regions for detailed comparison before and after using the proposed algorithm. Visually, the common appearance of speckle patterns in the single images has been significantly reduced in the averaged images.
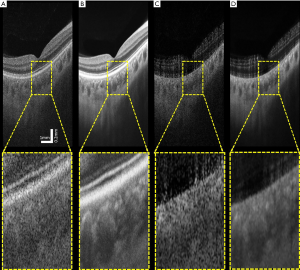
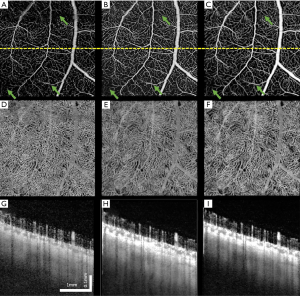
Figure 6 shows another example of human retina data, but located inferornasally to the fovea. Figure 6A,D,G are the enface images of retina, choriocapillaris and OCTA B-scan of a single volume. Figure 6B,E,H and Figure 6C,F,I are organized the same way as Figure 6A,D,G, but from volumes averaged three times and six times, respectively. Visually, the averaged en face images showed smoother vasculature, i.e., better connectivity, better contrast between vasculature and avascular regions. It is particularly evident that the disrupted retinal vasculatures on the single scan image, likely caused by patient movements, were significantly resolved and improved after registration and averaging, as indicated by green arrows.
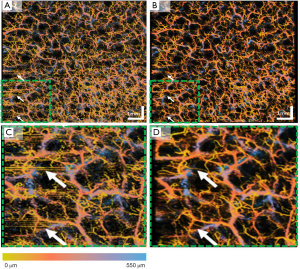
Apart from the human retina imaging, we have also tested this proposed algorithm on human skin imaging due to the increased usage of OCT/OCTA in dermatology applications. Figure 7 shows an example of en face OCTA image before and after registration and averaging. Similar to the human retina data, the averaged en face image shows less speckle noise, higher image contrast and better vascular connectivity. The inter-frame motion artifacts present on the single image (white arrows) have also removed after registration and averaging. Figure 7C,D show a zoomed-in region of the whole 9×9 mm scan. It can be visually observed that in the registered and averaged images, the presence of larger vessels from deeper layers (blue) is significantly enhanced compared to the single image. Moreover, the capillaries from superficial layers (yellow) also have a smoother appearance and less noisy.
The proposed algorithm works relatively fast. For 3D image registration, it took ~8 minutes to register 2 human skin OCT volumes (600×600×1,000) and 6 minutes to register 2 human retina volumes (500×500×1,000). For 2D images, it took ~6 seconds to register 2 human retina en face images (500×500). These processing times were assessed on a workstation configured with the Intel Xeon 2630-v3 CPU and 128G RAM.
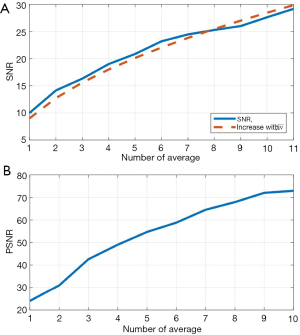
To evaluate further the performance of the proposed algorithm, PSNR and SNR were calculated using human skin data from all 5 subjects. As explained in the Methods section, there is a linear relationship between theoretical SNR value and the square root of iteration N. Such linear relationship is shown in Figure 8A (the orange dashed line). The experimentally calculated SNR values against is shown in Figure 8A (blue line), which agrees well with the theoretical ones. Figure 8B shows the experimentally calculated PSNR value against the iteration N. 11 registered volumes were used to generate this graph, PSNR describes how similar low quality images (the Ref1, Ave1, Ave2…Ave9 volumes) are to the highest quality image (Ave10 in Figure 3) base on Eq. [9]. The PNSRs over 4 averaged scans with the highest quality image are all over 50 dB, which indicates a very high similarity for and an early stop to acquire a high contrast image.
Other than the SNR and PSNR, the NCC has also been calculated using the human skin data. Table 1 shows the calculated NCC between individual scans on original, Affine, and Affine combined with B-spline transforms. The NCC was calculated for both OCT and OCTA volumes. Notably, the NCC values in OCTA data were lower than that in OCT volumes, this was likely due to the high frequency noise and motion artifacts that existed in the OCTA images, degrading the similarity between volumes.

Full table
Discussion
In this paper, we have presented a useful approach for multi-volume registration in OCT/OCTA, resulting in better averaging and noise reduction that would be useful for quantitative assessment of microvasculature features within tissue beds. The algorithm was designed for compensating the patient motion during and between each individual scans. Specifically, the proposed registration algorithm can minimize the spatial mismatch between repeated 3D scans, and align the volumes by using both affine and B-spline transformation. The affine transformation corrects the bulk motion, i.e., the global movement while the B-spline transformation compensates the local deformation. To increase the accuracy, stability and robustness of the algorithm we have also employed a multi-level resolution approach, in which the registration first starts on low resolution level and then the transformation calculated from lower resolution levels is being progressively applied to higher resolution levels. We have shown that such multi-level resolution approach has the advantage of speeding up the processing, important for in vivo imaging applications. As demonstrated by both retina and skin data, after registering and averaging multiple 3D OCT and OCTA volumes, the proposed algorithm could significantly reduce speckle noise and motion artifacts, yielding higher SNR, PSNR and NCC values.
The proposed registration algorithm has been shown very robust for two main reasons: (I) the combined use of Affine and B-spline strategies, and (II) the multi-level resolution treatments in the registration. We employed the combination of both Affine and B-spline registration after careful considerations of misalignments at the sources between OCT volumes. The Affine registration compensates for the global movement between individual repeated scans due to patient movement. And the B-spline registration aligns the local mismatches due to local movement. Specifically, the movements are the results of the heartbeat, respiration and other deformation of the tissue. The multi-level resolution treatment is specifically designed for considering how the OCT’s scanning protocol would influence motion patterns. In the OCT imaging protocol, multiple A-lines are used to form a B-scan and multiple B-scans would form a C-scan (3D volume). Therefore, when scanning a 3D sample, on the A-line direction, the motion is minimal (almost negligible) because the scanning speed is the fastest at the collection of A-scans. On the C-scan direction, the motion is the worst because the scanning speed is the slowest, and the B-scan direction is in between. This is why we designed the strategy to downsample the data differently at the A, B, and C scan directions. Comparing to a uniform downsampling, the proposed approach is efficient in reducing computational resources and increasing the stability of the algorithm on different samples. The number of downsampling levels and the iterations for parameters optimization can also be further optimized based on the cost function curves shown in Figure 7. For example, since the cost function for Affine transform converged on R1, it is not necessary to downsample four times. It is likely that with different type of OCT data, the required levels of downsampling for affine and B-spline transformation would also be different. Therefore, it is suggested that the optimal selection of downsampling levels is adjusted accordingly in terms of practical imaging situations.
Successful registration on both human skin data and human retina data from different OCT systems can also attest to the robustness of the proposed registration and averaging algorithm. Qualitatively, the averaging images are all shown with significantly less speckle noise and with line-like motion artifacts removed. On OCTA images, the connectivity of vasculature has been demonstrated to improve after averaging. The human skin data (Figure 7) revealed that the motion artifacts (the horizontal lines) are minimized and image contrast has been improved after averaging. For human retina data, Figure 5 showed that less speckle noise is present on OCT and OCTA B-scan images after registration and averaging. Particularly, the features of vessels and lumens in the choriocapillaris can be much clearly observed in averaged images. Figure 6 showed examples of en face projection images after the volumetric registration. On single scan OCTA images (Figure 6A,D), there are small broken endpoints and disconnectivity within capillary networks as well as obvious motion artifacts (green arrows). After 3 or 6 averages, vasculature connectivity has been significantly improved and previously present motion artifacts have also been compensated. It is expected that further quantification analysis based on averaged OCTA images could be much more reliable than single scan OCTA images. Quantitatively, we calculated SNR, PSNR and NCC as numerical descriptions of image quality. All three parameters have increased to a various extent with multiple averaging. Both qualitative and quantitative evidence strongly suggest that the proposed method can significantly improve OCT and OCTA image quality and potentially facilitate better clinical decision making.
Even though the proposed algorithm was designed for 3D data, it can also be applied to 2D images. Similar procedures have been reported in our previous study (5) with various constraints and parameters. The 2D registration requires fewer computation resources but it also requires layer segmentation as a step of image preprocessing. Moreover, with a 3D registration approach, it is likely that the extra depth information could be useful in some clinical settings. For example, the diagnosis and management of macular edema sometimes would require 3D OCT scans. In this case, this averaging approach could help obtain more accurate information of 3D tissue and vessel morphology.
There are a couple of advantages of our proposed algorithm comparing to previously published methods. Mostly, this proposed algorithm can be applied directly to OCT and OCTA data acquired from commercially available OCT systems. It does not require image preprocessing such as layer segmentation (23,24), or extra imaging hardware (16,18). Therefore, compared to previously published methods, it has a wider range of application possibilities. It can also be applied to data from other 3D imaging modalities such as ultrasound, MRI, multiphoton microscopy etc. Moreover, this approach does not require any particular scanning protocols such as orthogonal scanning requirement like in (22), though it can be applied to data acquired by any scanning protocols.
There are also some limitations of the proposed algorithm. Firstly, this algorithm is an intensity based registration algorithm, therefore it could fail if the intensity of images is too homogenous. Luckily, biological tissues usually have some unique features that can guide the registration and reduce unconstrained errors. Secondly, it is quite computationally expensive to register multiple 3D volumes. We have already utilized parallelization for optimization to improve the speed of the framework, but it still takes 60 minutes to register and average 10 OCT volumes under high quality setting, especially when each volume is as large as 600×600×2,560 pixels. There certainly exists a tradeoff between the quality of registration and the computational resources needed. With the same workstation set up, the time needed for registration can be adjusted by optimizing the number of downsampling levels and the number of iterations according to practical situations. The future development is to implement the proposed algorithm on a GPU platform (39) to further improve the speed. Lastly, the proposed registration algorithm is not boundless, meaning that a certain amount of overlap between images is need to succeed. For our collected human retina data, the motion tracking feature was turned on during acquisition; and for our collected human skin data, the portable probe was attached to the samples to avoid large subject movements. We did not observe any failures of registration on our collected data, but if the inter-volume motion is too large, this proposed algorithm can certainly experience errors or failures.
In conclusion, we have proposed a 3D registration method and demonstrated its robustness on reducing speckle noises and suppressing motion artifacts. Both human skin data and retina data were collected from different OCT systems to test the robustness of this proposed algorithm. Averaged OCTA data showed higher contrast of vascular network and better connectivity for vessels of all sizes, as evidenced by the resulting higher SNR, PSNR and NCC metrics. It is expected that the proposed algorithm would be practically useful in better visualization and more reliable quantification of in vivo OCT and OCTA data, which could be beneficial to research and clinical applications of OCT.
Acknowledgments
Funding: This work was supported in part by the National Institutes of Health with a contract from National Eye Institute (R01-EY028753), Carl Zeiss Meditec Inc., and an unrestricted grant from the Research to Prevent Blindness, Inc., New York, NY, USA. The funding organization had no role in the design or conduct of this research.
Footnote
Provenance and Peer Review: With the arrangement by the Guest Editors and the editorial office, this article has been reviewed by external peers.
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at http://dx.doi.org/10.21037/qims-20-751). The special issue “Advanced Optical Imaging in Biomedicine” was commissioned by the editorial office without any funding or sponsorship. RKW served as the unpaid Guest Editor of the special issue and serves as an unpaid Deputy Editor of Quant Imaging Med Surg. The authors have no other conflicts of interest to declare.
Ethical Statement: The subject imaging followed protocols reviewed and approved by the Institutional Review Board of Medical Sciences Subcommittee at the University of Washington, Seattle. The tenets of the Declaration of Helsinki and Health Insurance Portability and Accountability Act were followed. Informed consent forms were obtained from all subjects before participation.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- de Oliveira Dias JR, Zhang Q, Garcia JM, Zheng F, Motulsky EH, Roisman L, Miller A, Chen CL, Kubach S, de Sisternes L. Natural history of subclinical neovascularization in nonexudative age-related macular degeneration using swept-source OCT angiography. Ophthalmology 2018;125:255-66. [Crossref] [PubMed]
- Kashani AH, Chen CL, Gahm JK, Zheng F, Richter GM, Rosenfeld PJ, Shi Y, Wang RK. Optical coherence tomography angiography: A comprehensive review of current methods and clinical applications. Prog Retin Eye Res 2017;60:66-100. [Crossref] [PubMed]
- Roisman L, Zhang Q, Wang RK, Gregori G, Zhang A, Chen CL, Durbin MK, An L, Stetson PF, Robbins G, Miller A, Zheng F, Rosenfeld PJ. Optical coherence tomography angiography of asymptomatic neovascularization in intermediate age-related macular degeneration. Ophthalmology 2016;123:1309-19. [Crossref] [PubMed]
- Miller AR, Roisman L, Zhang Q, Zheng F, de Oliveira Dias JR, Yehoshua Z, Schaal KB, Feuer W, Gregori G, Chu Z. Comparison between spectral-domain and swept-source optical coherence tomography angiographic imaging of choroidal neovascularization. Invest Ophthalmol Vis Sci 2017;58:1499-505. [Crossref] [PubMed]
- Chu Z, Zhou H, Cheng Y, Zhang Q, Wang RK. Improving visualization and quantitative assessment of choriocapillaris with swept source OCTA through registration and averaging applicable to clinical systems. Sci Rep 2018;8:16826. [Crossref] [PubMed]
- Zhang Q, Shi Y, Zhou H, Gregori G, Chu Z, Zheng F, Motulsky EH, De Sisternes L, Durbin M, Rosenfeld PJ. Accurate estimation of choriocapillaris flow deficits beyond normal intercapillary spacing with swept source OCT angiography. Quant Imaging Med Surg 2018;8:658. [Crossref] [PubMed]
- Wang RK, Jacques SL, Ma Z, Hurst S, Hanson SR, Gruber A. Three dimensional optical angiography. Opt Express 2007;15:4083-97. [Crossref] [PubMed]
- Deegan AJ, Talebi-Liasi F, Song S, Li Y, Xu J, Men S, Shinohara MM, Flowers ME, Lee SJ, Wang RK. Optical coherence tomography angiography of normal skin and inflammatory dermatologic conditions. Lasers Surg Med 2018;50:183-93. [Crossref] [PubMed]
- Tan HEI, Santa Maria PL, Wijesinghe P, Francis Kennedy B, Allardyce BJ, Eikelboom RH, Atlas MD, Dilley RJ. Optical coherence tomography of the tympanic membrane and middle ear: a review. Otolaryngol Head Neck Surg 2018;159:424-38. [Crossref] [PubMed]
- Le NM, Song S, Zhou H, Xu J, Li Y, Sung CE, Sadr A, Chung KH, Subhash HM, Kilpatrick L. A noninvasive imaging and measurement using optical coherence tomography angiography for the assessment of gingiva: An in vivo study. J Biophotonics 2018;11:e201800242. [Crossref] [PubMed]
- Vignali L, Solinas E, Emanuele E. Research and clinical applications of optical coherence tomography in invasive cardiology: a review. Current cardiology reviews 2014;10:369-76. [Crossref] [PubMed]
- Spaide RF, Fujimoto JG, Waheed NK. Image artifacts in optical coherence angiography. Retina (Philadelphia, Pa) 2015;35:2163. [Crossref] [PubMed]
- Chu Z, Lin J, Gao C, Xin C, Zhang Q, Chen CL, Roisman L, Gregori G, Rosenfeld PJ, Wang RK. Quantitative assessment of the retinal microvasculature using optical coherence tomography angiography. J Biomed Opt 2016;21:66008. [Crossref] [PubMed]
- Li P, Cheng Y, Zhou L, Pan C, Ding Z, Li P. Single-shot angular compounded optical coherence tomography angiography by splitting full-space B-scan modulation spectrum for flow contrast enhancement. Opt Lett 2016;41:1058-61. [Crossref] [PubMed]
- Wang RK, Zhang A, Choi WJ, Zhang Q, Chen CL, Miller A, Gregori G, Rosenfeld PJ. Wide-field optical coherence tomography angiography enabled by two repeated measurements of B-scans. Opt Lett 2016;41:2330-3. [Crossref] [PubMed]
- Li P, Cheng Y, Li P, Zhou L, Ding Z, Ni Y, Pan C. Hybrid averaging offers high-flow contrast by cost apportionment among imaging time, axial, and lateral resolution in optical coherence tomography angiography. Opt Lett 2016;41:3944-7. [Crossref] [PubMed]
- Wong A, Mishra A, Bizheva K, Clausi DA. General Bayesian estimation for speckle noise reduction in optical coherence tomography retinal imagery. Opt Express 2010;18:8338-52. [Crossref] [PubMed]
- Sheehy CK, Yang Q, Arathorn DW, Tiruveedhula P, de Boer JF, Roorda A. High-speed, image-based eye tracking with a scanning laser ophthalmoscope. Biomed Opt Express 2012;3:2611-22. [Crossref] [PubMed]
- Kocaoglu OP, Ferguson RD, Jonnal RS, Liu Z, Wang Q, Hammer DX, Miller DT. Adaptive optics optical coherence tomography with dynamic retinal tracking. Biomed Opt Express 2014;5:2262-84. [Crossref] [PubMed]
- Cheng Y, Guo L, Pan C, Lu T, Hong T, Ding Z, Li P. Statistical analysis of motion contrast in optical coherence tomography angiography. J Biomed Opt 2015;20:116004. [Crossref] [PubMed]
- Potsaid B, Gorczynska I, Srinivasan VJ, Chen Y, Jiang J, Cable A, Fujimoto JG. Ultrahigh speed spectral/Fourier domain OCT ophthalmic imaging at 70,000 to 312,500 axial scans per second. Opt Express 2008;16:15149-69. [Crossref] [PubMed]
- Kraus MF, Potsaid B, Mayer MA, Bock R, Baumann B, Liu JJ, Hornegger J, Fujimoto JG. Motion correction in optical coherence tomography volumes on a per A-scan basis using orthogonal scan patterns. Biomed Opt Express 2012;3:1182-99. [Crossref] [PubMed]
- Zang P, Liu G, Zhang M, Wang J, Hwang TS, Wilson DJ, Huang D, Li D, Jia Y. Automated three-dimensional registration and volume rebuilding for wide-field angiographic and structural optical coherence tomography. J Biomed Opt 2017;22:26001. [Crossref] [PubMed]
- Hendargo HC, Estrada R, Chiu SJ, Tomasi C, Farsiu S, Izatt JA. Automated non-rigid registration and mosaicing for robust imaging of distinct retinal capillary beds using speckle variance optical coherence tomography. Biomed Opt Express 2013;4:803-21. [Crossref] [PubMed]
- Lezama J, Mukherjee D, McNabb RP, Sapiro G, Kuo AN, Farsiu S. Segmentation guided registration of wide field-of-view retinal optical coherence tomography volumes. Biomed Opt Express 2016;7:4827. [Crossref] [PubMed]
- Wang G, Le NM, Hu X, Cheng Y, Jacques SL, Subhash H, Wang RK. Semi-automated registration and segmentation for gingival tissue volume measurement on 3D OCT images. Biomed Opt Express 2020;11:4536-47. [Crossref] [PubMed]
- Niemeijer M, Garvin MK, Lee K, van Ginneken B, Abràmoff MD, Sonka M. Registration of 3D spectral OCT volumes using 3D SIFT feature point matching. Lake Buena Vista (Orlando Area), Florida: Image Processing, 2009.
- Staring M, Klein S, Pluim JP. A rigidity penalty term for nonrigid registration. Med Phys 2007;34:4098-108. [Crossref] [PubMed]
- Thévenaz P, Unser M. Optimization of mutual information for multiresolution image registration. IEEE Trans Image Process 2000;9:2083-99. [Crossref] [PubMed]
- Klein S, Pluim JP, Staring M, Viergever MA. Adaptive stochastic gradient descent optimisation for image registration. Int J Comput Vis 2009;81:227. [Crossref]
- Lester H, Arridge S. A survey of hierarchical non-linear medical image registration. Pattern Recognit 1999;32:129-49. [Crossref]
- Klein S, Staring M, Murphy K, Viergever MA, Pluim JP. Elastix: a toolbox for intensity-based medical image registration. IEEE Trans Med Imaging 2010;29:196-205. [Crossref] [PubMed]
- Wei DW, Deegan AJ, Wang RK. Automatic motion correction for in vivo human skin optical coherence tomography angiography through combined rigid and nonrigid registration. J Biomed Opt 2017;22:66013. [Crossref] [PubMed]
- Zhang Q, Huang Y, Zhang T, Kubach S, An L, Laron M, Sharma U, Wang RK. Wide-field imaging of retinal vasculature using optical coherence tomography-based microangiography provided by motion tracking. J Biomed Opt 2015;20:066008. [Crossref] [PubMed]
- Wang RK, An L, Francis P, Wilson DJ. Depth-resolved imaging of capillary networks in retina and choroid using ultrahigh sensitive optical microangiography. Opt Lett 2010;35:1467-9. [Crossref] [PubMed]
- An L, Subhush H, Wilson D, Wang R. High-resolution wide-field imaging of retinal and choroidal blood perfusion with optical microangiography. J Biomed Opt 2010;15:026011. [Crossref] [PubMed]
- Yin X, Chao JR, Wang RK. User-guided segmentation for volumetric retinal optical coherence tomography images. J Biomed Opt 2014;19:086020. [Crossref] [PubMed]
- Chu Z, Zhang Q, Zhou H, Shi Y, Zheng F, Gregori G, Rosenfeld PJ, Wang RK. Quantifying choriocapillaris flow deficits using global and localized thresholding methods: a correlation study. Quant Imaging Med Surg 2018;8:1102. [Crossref] [PubMed]
- Shamonin DP, Bron EE, Lelieveldt BP, Smits M, Klein S, Staring M. Fast parallel image registration on CPU and GPU for diagnostic classification of Alzheimer's disease. Front Neuroinform 2014;7:50. [PubMed]


