Three-dimensional characterizations of two-photon excitation fluorescence images of elastic fibers affected by cutaneous scar duration
Introduction
The scar is a product of wound healing (1,2), and the formation of scars is generally considered a process of granulation tissue fibrosis and increasing deposition of collagen and elastic fibers. However, the deep mechanism of the wound healing process is still a mystery. Cutaneous scars not only have an aesthetic dimension but can also restrict normal skin psychological function. Scar treatment has long been a research focus, and many practical and effective methods such as laser treatment have become clinical therapies; however, the different treatment methods are usually suitable only for specific types of scars. Classifying the type or duration of scars, some traditional methods such as biopsies and long-term observation have inevitable drawbacks such as secondary trauma or inaccuracy. With the development of microscopy and computer science, visualization in scientific computing based on microscopic images has been a hot research topic. Elastic fibers are long, thin, highly refractive extracellular components of connective tissue. They are composed of the protein elastin and usually branch and anastomose freely. Unlike the stronger and non-extensible collagen fibers, elastic fibers can be stretched from one and one-third to one and one-half times their normal length and, when released, return to their normal length. Elastic fibers (3) provide the elasticity and mobility of organs such as the skin, blood vessels, elastic ligaments, and the external ear’s cartilage.
Under the action of a femtosecond laser, the non-linear optical effects of the internal components of biological tissue have been used to study scar formation and development, as well as the internal laws of wound repair, which has promoted a deeper understanding of the scar formation mechanism utilizing early, direct and non-destructive detection, diagnosis and real-time monitoring. The advantages of two-photon excitation fluorescence (TPEF) microscopy have greatly expanded its application in biological systems. First, TPEF provides high internal three-dimensional (3D) resolution, limiting phototoxicity, photodamage, and photobleaching to focal points, thus allowing it to be used for observation for longer periods. Second, because the excitation wavelength of TPEF is very different from the emission wavelength, the excitation laser can be effectively filtered out to obtain a higher signal-to-noise ratio. Third, because TPEF does not need additional confocal pinholes, most dispersed photons can be detected, thus improving the collection of the fluorescence signals’ efficiency. Also, considering that the TPEF spectrum of many fluorescent molecules is wider than the single-photon excitation spectrum, it is possible to excite various fluorescent molecules with a single wavelength, thus obtaining more image information. Moreover, tissue absorption in the near-infrared window (700–1,000 nm) is relatively small, giving TPEF a deeper penetration depth (4-6).
Many researchers have studied descriptions of 2D microscopic images. Some features such as phase parameters and texture feature parameters have already been presented. There are numerous texture analysis methods, such as grey level co-occurrence matrix (GLCM) (7), local binary pattern (LBP) (8), binary gradient contours (BGC) (9), local ternary pattern (LTP) (10,11), improved local ternary pattern (ILTP) (12). Many methods have achieved fantastic results, but all 2D analysis methods have inevitable drawbacks. Medical section plane images from the surface to depth are correlated, and analysis of one of them would unnecessarily fall into locality, imperfection, even inaccuracy. Aiming at solving the problems with 2D analysis, some researchers have presented 3D analysis methods (13-16). Borrelli et al. presented two 3D parameters (3D vascular volume and 3D perfusion density) to analyze optical coherence tomography angiography images to measure macular ischemia in eyes affected by non-proliferative diabetic retinopathy (17). Varando et al. developed a new tool, MultiMap, which allows visualization, 3D segmentation, and quantification of fluorescent structures selectively in the neuropil from large stacks of confocal microscopy images (18). Hasaballa et al. explored 3D quantification of myocardial collagen morphology from confocal images and presented some morphological parameters, including elongation, flatness, and anisotropy, based on the covariance matrix of 3D images (19). Liu et al. developed a metric, 3D directional variance, as a quantitative biomarker of truly 3D organization of fiber-like structures (20).
In this study, we investigated the 3D quantification of elastic fibers in cutaneous scar tissue to understand how they changed with scar duration. This study’s procedure had three main steps: preprocessing and segmentation, 3D reconstruction and skeleton extraction, and quantitative analysis. Finally, the application of random forests regression analysis in the prediction of scar duration was studied.
Methods
Ethics approval
This study of human tissue imaging was approved by the Fujian Normal University Research Ethics Board (no. 2018-3-3). Each volunteer subject gave informed consent, and the study strictly conformed to institutional rules governing the clinical investigation of human subjects in biomedical research.
Specimen preparation and acquisition
Ex vivo human cutaneous scar samples were obtained from 30 female patients who had undergone cesarean section or abdominal cholecystectomy 2–22 years previously, and each of the six duration groups had five patients (Table 1). The samples were snap-frozen in liquid nitrogen (–196 °C) immediately after excision.
Full table
High-resolution images were obtained with a TPEF microscopic imaging system on a commercial LSM 510 META (Zeiss, Inc.) coupled to a mode-locked Ti: sapphire laser (110 fs,76 MHz), operated at 810 nm (Coherent Mira 900-F). The META detector had eight independent channels, and each of them could be set to detect backscattered intrinsic TPEF signals. An independent channel was selected to obtain the high-resolution images: one channel with a wavelength from 430 to 697 nm to collect the TPFF signals. To obtain sequential images (16 sequential 2D images with depth intervals of 2 µm between two adjacent images) to reconstruct the 3D images, the device’s focal plane (Z-level) needed to be changed at different depths. The scar’s central area was focused on for imaging, and several images were obtained within the same scar sample for averaging. The obtained images (512×512 pixels) were obtained at 2.5 µs/pixel with a 12-bit depth.
Proposed method of analysis
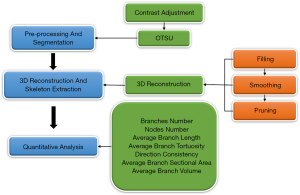
The image analysis method was developed in the context of its application to the 3D confocal microscopy images of elastic fibers in human cutaneous scars. With this method, we extracted some quantitative 3D information of elastic fibers, such as the length and diameter of fibers and the number of branches and nodes. An outline of our approach is shown in Figure 1. The first stage comprised preprocessing and segmentation of sequential microscopy images. The second stage was the 3D reconstruction and thinning process, which contained a range of processing steps for better reconstruction performance and more accurate extracted quantitative information. Finally, the quantitative was extracted on the foundation of the first two steps. We implemented our method in Visual Studio 2015, VTK 7.0.0, MATLAB R2014b, and ran it on a PC with a 3.2 GHz Core CPU and 8 GB RAM.
Stage 1: preprocessing
The 2D images were processed mainly to extract the region of interest (ROI) and converted to binary images for further processing. Using the microscopy image and elastic fibers’ characteristics, we designed a pipeline of preprocessing and segmentation as follows. The first was increasing the contrast of the images to highlight the ROIs, and the second step was generating the binary image based on the OTSU algorithm and suppressing small noise through elaborating the small object region by setting a threshold.
Stage 2: 3D reconstruction and skeleton extraction
To better understand the microstructure and alterations of elastic fibers within the normal cutaneous scar, we reconstructed 3D images of elastic fibers from the different scar types as listed in Table 1. Computerized 3D visualization mainly studies the generation and visualization of volume data from slice-based image data generated by laser scanning confocal microscopy. The 3D visualization technique, as a mature technology, can be split into two categories: surface rendering and volume rendering. Surface rendering firstly extracts the isosurface as intermediate and then uses it to fit the 3D image. The fundamental difference of volume rendering compared with surface rendering is that there is no intermediate generation, and all voxels can contribute to the final visualized result. In this study, we used four different 3D reconstruction algorithms, comprising Contour Matching algorithm (21), Marching Cubes (22,23), Ray Casting Volume Rendering (24), and Dividing Cubes algorithm (25), to reconstruct the 3D elastic fiber images.
After 3D reconstruction, the skeleton of the output fibrin network was extracted using a 3D thinning algorithm (26,27). The algorithm was mainly to iteratively remove voxels on the boundaries until a 1-voxel-wide medial axis was left and did not change the networks’ topological structure. However, it is well known that this algorithm is sensitive to noise and some fake branches occurred caused by perturbations and deformations on the object boundaries. These fake branches have a severe effect on the accuracy of statistical data, such as the number of branches, which will be much increased, and the average length of the branches will be shortened for lots of the short fake branches, and so on. To solve these problems, we adopted three methods: filling, smoothing, and pruning. The first problem was that there were many small holes in the volume, which led to many fake nodes and branches, and as a solution, we chose to fill the holes of the volume data.
With regard to smoothing, we found that the rough surface of the 3D image caused burrs, and we adopted a closing operation in the 3D morphological processing to solve this problem. The final method was pruning, which removed segments with a length less than the average thickness. After these processing procedures, we obtained the refined skeleton of the 3D image.
Stage 3: extraction of quantitative information
The final step was mainly to extract significant morphological alterations of the scar samples of different durations and analyze the possible effects of these discrepancies. Based on the characteristics of the 3D skeleton image, we extracted a series of 3D morphological feature parameters: branches number (B-NUM), nodes number (N-NUM), average branch linear length (AB-LL), average branch broken-line length (AB-BL), average branch tortuosity (AB-T), branch direction consistency (B-DC), average branch volume (AB-V), and average branch sectional area (AB-SA). Our analysis’s foundation transformed from a 3D skeleton image to a 3D graph with detailed branches and nodes information. The extraction methods of the different parameters are described as follows.
B-NUM and N-NUM
The first two parameters can be directly obtained from the 3D graph. N-NUM was defined as the total number of branch nodes, and B-NUM as the total number of branches.
AB-LL and AB-BL
AB-LL was defined as the Euclidean distance between the start and endpoints of a branch in 3D data space. AB-BL was defined as the sum of the Euclidean distance of pixel-to-pixel from the start to the end of one branch in 3-D data space. We used D (N1, N2) to refer to the Euclidean distance of point N1 and point N2 in the 3D dataset defined as follows:
where N1(x1, y1, z1) and N2 (x2, y2, z2) are two points in the 3D dataset. The two parameters above can be defined as:
where I represents one branch and is made up of N sequential pixels. Ii denotes the coordinate of the ith pixel of the branch. D(I) and B(I) are the linear length and the broken-line length, respectively, of the specified skeleton branch.
AB-LL was defined as the mean value of the sum of all branches’ broken-line lengths because AB-BL can truly represent one branch’s practical length.
AB-T
After the two types of branch length were defined, we defined AB-T as:
where T(I) represents the tortuosity of branch I. As can be seen, T(I) is between 0 and 1, and a value closer to 1 indicates the branch is straighter. This parameter indicated the possible alteration in-branch tortuosity after the different duration of scars.
AB-T was also calculated as the mean value of the sum of all branches’ tortuosity.
B-DC
We defined B-DC as the direction of a straight line from the start to the endpoint in one branch. After that, B-DC can be defined as the distribution of angle θ between the branch vector VI and the fixed vector specified as VC (1,1,1). The cosine value of angle θ can be calculated as:
where (x1, y1, z1) and (x2, y2, z2) are coordinates of the start and endpoints, respectively, of a branch as mentioned above. If two results had the same absolute value, whether positive or negative, it indicated they were parallel and had the same trend. Therefore, we chose the absolute value to display in the next step.
AB-V
The next parameter was the branch’s volume, which was defined as the voxels number of the branch. Acquiring the parameter was a search procedure of points satisfying certain conditions based on the node’s information in the 3D skeleton graph. The searching started from the skeleton’s central point and proceeded in two opposite directions along with the skeleton. The process of searching algorithm is shown in Table 2.

Full table
According to the upper search procedure, we obtained the final AX set, which contained all branch points. We used the number of no-zeros points instead of the number of voxels to estimate the branch’s volume because of the unknown distribution of voxels.
As before, AB-V was defined as the mean value of all branches’ volumes.
AB-SA
After obtaining the volume, the sectional area of the branch can be defined as the result of the branch volume divided by the length of the corresponding skeleton, which is expressed as follows:
where VI denotes the branch’s volume, and I and BI represent the broken-line length as defined above. AI measures the thickness branch I.
AB-SA was defined as the mean value of the sum of all branches’ sectional areas.
Stage 4: random forests for regression
As an ensemble learning algorithm for classification, regression, and other tasks, random forests are a group of decision trees and have been widely used in many applications. Every decision tree of the forest will vote for the final result; when used in classification, the final outcome is the label with the most votes, whereas, in regression, the final outcome is the average of the individual tree predictions. Random forests are not easily overfitting machine learning algorithms that mainly depend on its radical random mechanism. When training the random forest bagging algorithm was used to generate the random training set. Also, randomly selected mtry characteristics further guarantee the randomness of the forest. Excepting the parameter mtry, parameter K, representing the number of decision trees, also affects random forests’ performance. Random forests also have a prominent characteristic: random forests can rank a variable according to its importance, so this characteristic means random forests can be used in feature engineering.
In our study, random forests’ performance was studied with the alterations of parameters K and R2, and the root-mean-square error (RMSE) was used to estimate the performance.
Results
Each of the six groups of scar duration included five different image sequences from the five patients. Figure 2 shows the main process: 2D TPEF image sequence, 3D reconstructed image, and 3D skeleton extraction image.

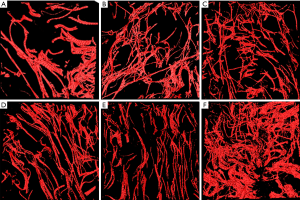
In the first step, we reconstructed 3D images of elastic fibers, and representative 3D reconstructed elastic fiber TPEF images from normal human scars of 2, 5, 8, 10, 21, and 22 years duration after cesarean section are presented in Figure 3. Through our comparison of the reconstruction results, we found that volume rendering had the features of fast rendering speed, and was smooth but easily fractured, and surface rendering had the features of low rendering speed that was, rough but more integrated. From these reconstructed images, we can easily see some obvious morphological changes with duration. For example, the distribution of the elastic fibers in 3D space becomes progressively denser, and the thickness of the branches seems to become thinner over the 20 years. These changes are obvious features displayed in the images, but some other characteristics are not easily observed directly, for which we need some quantitative data.
3D thinning results and improvements for morphological analysis
Figure 4 displays 3D reconstructed results before and after improvement. Fake branches and burrs have been well pruned.

Application of random forests regression
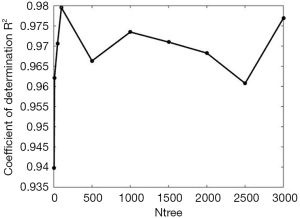
Random forests regression analysis was applied to predict scar duration using the extracted parameters of the 30 samples. The average value of every parameter in scars of different duration is listed in Table 3. From the table, we found that several parameters had an explicit changing rule while some did not. B-NUM and N-NUM increased with time, AB-LL, AB-BL, AB-V, AB-SA were in reverse order, and AB-T and B-DC did not show a clear regular change. As discussed earlier, random forests have better predicting and assessing features in regression problems. In random forests, the parameters mtry and ntree have an important role. To explore the relationship between ntree and random forests’ performance, we fixed ntree =5, 10, 50, 100, 500, 1,000, 1,500, 2,000, 2,500, and 3,000 as depicted in Figure 5. We observed that after ntree=100, random forests’ performance remained stable with little fluctuation, so we need to set ntree=100 to satisfy the requirement without needing any more decision trees.
Full table
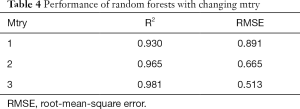
Next, to determine the appropriate parameter mtry, we explored random forests’ performance when mtry =1, 2, and 3 and ntree =100 as depicted in Table 4. We observed that when mtry =3, random forests had a better fitting performance with R2=0.981 and RMSE =0.513 when ntree =100 and mtry =3.
Full table
Discussion
We explored how to quantify the 3D morphological changes of elastic fibers in cutaneous scars over time. This study’s main procedure can be split into four steps: 3D reconstruction, skeleton extraction, quantitative information extraction, and random forests regression. The first step, 3D reconstruction, mainly achieved a 3D image of elastic fiber in dermal tissue but did not influence quantitative information accuracy. The second step, skeleton extraction, is mainly applied as a bridge between visualization and calculation and has an important influence on quantitative information accuracy. Aiming at overcoming the drawbacks of the existing 3D thinning algorithm, we propose three improvements: filling, smoothing, and pruning. As shown in Figure 4, the skeleton of the original 3D image becomes much more unambiguous, which means much more accurate quantitative information can be extracted. The third step, quantitative information extraction, mainly extracted eight parameters: number of branches, number of nodes, mean length and tortuosity of branches, congruency of branches direction, the volume of branches, and the mean sectional area of branches. The fourth step, random forests regression, is mainly applied to explore the prediction of scar duration. Figure 5 shows the performance of random forests with changing duration, and the result indicated that K=100 satisfied the requirement of this study. Table 4 shows the performance of random forests with mtry =1, 2, and 3 when K=100, and the result indicated that mtry =3 and K=100 had the best fitting performance. Table 4 also compares random forests and unitary regression models, and the result showed that random forests with multiple parameters had better performance in predicting scar duration than unitary regression with only one parameter.
To verify the effectiveness of our 3D characterization method for TPEF images of elastic fibers in the future, more samples for more effective model development, the importance of the parameters, the effect of patients’ ages on the growth and distribution of elastic fibers, and the 3D characterization for pathologic scars are future research.
Conclusions
In this study, a process for quantitatively analyzing 3D elastic fibers of human scars was designed, comprising 3D reconstruction, skeleton extraction, quantitative analysis, and random forests regression. Our findings demonstrated that the parameters we extracted had a distinct relationship with scar duration and that random forests had better performance in forecasting scar duration than unitary models.
Acknowledgments
Funding: The authors gratefully acknowledge the financial supports of the Fund for High-level Talents of the Xiamen University of Technology (No. YKJ19010R), the Natural Science Foundation of Fujian Province (2018J01784, 2019J01272), the United Fujian Provincial Health and Education Project for Tackling the Key Research of China (2019-WJ-03) and the Fujian Provincial Health and Family Planning of Young and Middle Age Personnel Training Projects (2016-ZQN-27).
Footnote
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at http://dx.doi.org/10.21037/qims-20-1051). The authors have no conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013). This study of human tissue imaging was approved by the Fujian Normal University Research Ethics Board (no. 2018-3-3). Informed consent was obtained from each volunteer subject.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Tsao SS, Dover JS, Arndt KA, Kaminer MS. Scar management: keloid, Hyper trophic, atrophic, and acne scars. Semin Cutan Med Surg 2002;21:46-75. [Crossref] [PubMed]
- Roten SV, Bhat S, Bhawan J. Elastic fibers in scar tissue. J Cutan Pathol 1996;23:37-42. [Crossref] [PubMed]
- Johnson EF, Chetty K, Moore IM, Stewart A, Jones W. The distribution and arrangement of elastic fibres in the intervertebral disc of the adult human. J Anat 1982;135:301-9. [PubMed]
- Sun Y, You S, Du X, Spaulding A, Liu ZG, Chaney EJ, Spillman DR Jr, Marjanovic M, Tu H, Boppart SA. Real-time three-dimensional histology-like imaging by label-free nonlinear optical microscopy. Quant Imaging Med Surg 2020;10:2177-90. [Crossref] [PubMed]
- Lin HX, Yang LJ, Zhang X, Liu GM, Zhuo SM, Chen JX, Song JB. Emerging Low-Dimensional Nanoagents for Bio-Microimaging. Advanced Functional Materials 2020;30:2003147 [Crossref]
- Lin H, Fan T, Sui J, Wang G, Chen J, Zhuo S, Zhang H. Recent advances in multiphoton microscopy combined with nanomaterials in the field of disease evolution and clinical applications to liver cancer. Nanoscale 2019;11:19619-35. [Crossref] [PubMed]
- Mohanaiah P, Sathyanarayana P, Gurukumar L. Image texture feature extraction using GLCM approach. Int J Sci Res Publications 2013;3:1-5.
- Ojala T, Pietikainen M, Maenpaa T. Multiresolution gray-scale and rotation invariant texture classification with local binary pattern. IEEE Trans PAMI 2002;24:971-87. [Crossref]
- Fernández A, Álvarez MX, Bianconi F. Image classification with binary gradient contours. Opt Lasers Eng 2011;49:1177-84. [Crossref]
- Guo Z, Zhang L, Zhang D. A completed modeling of local binary pattern operator for texture classification. IEEE Trans Image Process 2010;19:1657-63. [Crossref] [PubMed]
- Tan X, Triggs B. Enhanced local texture feature sets for face recognition under difficult lighting conditions. IEEE Trans Image Process 2010;19:1635-50. [Crossref] [PubMed]
- Nanni L, Brahnam S, Lumini A. A local approach based on a Local Binary Patterns variant texture descriptor for classifying pain states. Expert Syst Appl 2010;37:7888-94. [Crossref]
- Campagnola PJ, Millard AC, Terasaki M, Hoppe PE, Mohler WA. Three-dimensional high-resolution second-harmonic generation imaging of endogenous structural proteins in biological tissues. Biophys J 2002;82:493-508. [Crossref] [PubMed]
- . Königa1 K, Schenke-Layland K, Riemann I, Stock UA. Multiphoton autofluorescence imaging of intratissue elastic fibers. Biomaterials 2005;26:495-500. [Crossref]
- Mostaço-Guidolin LB, Ko ACT, Wang F, Xiang B, Hewko M, Tian GH, Major A, Shiomi M, Sowa MG. Collagen morphology and texture analysis: from statistics to classification. Sci Rep 2013;3:2190. [Crossref] [PubMed]
- Cai S, Tian Y, Lui H, Zeng H, Wu Y, Chen G. Dense-UNet: a novel multiphoton in vivo cellular image segmentation model based on a convolutional neural network. Quant Imaging Med Surg 2020;10:1275-85. [Crossref] [PubMed]
- Borrelli E, Sacconi R, Querques L, Battista M, Querques G. Quantification of diabetic macular ischemia using novel three-dimensional optical coherence tomography angiography metrics. J Biophotonics 2020;13:e202000152 [Crossref] [PubMed]
- Varando G, Benavides-Piccione R, Muoz A, Kastanauskaite A, Defelipe J. MultiMap: A Tool to Automatically Extract and Analyse Spatial Microscopic Data From Large Stacks of Confocal Microscopy Images. Front Neuroanat 2018;12:37. [Crossref] [PubMed]
- Hasaballa AI, Sands GB, Wilson AJ, Young AA, Wang VY, LeGrice IJ, Nash MP. Three-Dimensional Quantification of Myocardial Collagen Morphology from Confocal Images. International Conference on Functional Imaging and Modeling of the Heat 2017; 10263. Springer, Cham.
- Liu Z, Pouli D, Sood D, Sundarakrishnan A, Mingalone CKH, Arendt LM, Alonzo C, Quinn KP, Kuperwasser C, Zeng L. Automated quantification of three-dimensional organization of fiber-like structures in biological tissues. Biomaterials 2017;116:34-47. [Crossref] [PubMed]
- Fuchs H, Kedem ZM, Uselton SP. Optimal surface reconstruction from planar contours. Communications of the ACM 1977;20:693-702. [Crossref]
- Lorensen WE, Cline HE. Marching cubes: a high resolution 3d surface construction algorithm. Computer Graphic 1987;21:163-9. [Crossref]
- Dürst MJ. Additional reference to "Marching Cubes". Computer Graphics 1988;22:72-3. [Crossref]
- Harvey R, Pfister H. Ray Casting Architectures for Volume Visualization. IEEE Trans Vis Comput Graph 1999;5:210-23. [Crossref]
- Ellis CH, Siegwalt L, Edward LW. Dividing cubes and method for the display of surface structures contained within the interior region of a solid body. European Patent EP 0216156[P]: 1993-12-15.
- Lee TC. Building skeleton models via 3-D medial surface/axis thinning algorithm. Graphical Models Image Process 1994;56:462-78. [Crossref]
- Lobregt S, Verbeek PW, Groen FCA. Three-dimensional skeletonization: Principle and algorithm. IEEE Trans Pattern Anal Mach Intell 1980;2:75-7. [Crossref] [PubMed]