
Spectral response of optical fiber probe with closely spaced fibers
Introduction
The ability to assess a tissue’s status by a quick low-cost non-invasive optical measurement can find many uses in clinical medicine. Optical spectroscopy can monitor inflammation (1), edema (2), assess metabolic consumption of oxygen (3), detect nuclear abnormalities (4), and quantify fibrosis or stromal remodeling, to mention a few examples. Optical fiber spectrometers are especially convenient for topical placement of a probe to characterize a tissue site, for example on skin (5), oral cavity (1), uro-genital (6), gastrointestinal tract (7), brain (8,9), breast (10), kidney (11), liver (12), and bronchi (13).
This report considers the use of closely spaced optical fibers in a spectroscopic probe, one fiber for light delivery and one fiber for light collection. The fiber separation is less than 1 mm, which interrogates a local tissue site. Bigio and colleagues pioneered such spectroscopy (14-16), which is especially sensitive to the light scattering properties of a tissue and is called Elastic Scattering Spectroscopy (ESS).
A two-fiber probe on a tissue site delivers light into the tissue with one optical fiber and collects light with the second optical fiber. The lateral separation between the two optical fibers as they contact the tissue determines the tissue depth that the measurement interrogates. Larger separation yields a deeper measurement. Closer separation yields a more superficial measurement. The interaction of the probe response with the inter-fiber separation and the wavelength-dependent tissue optical properties are quite non-linear (17). Therefore, light transport theory is used to understand the interaction and to interpret measurements.
Diffusion theory provides a simple light transport calculation that usually works well when the fiber separation is greater than 1 or 2 mm. Often one wishes a more compact probe where the optical fiber separation is much closer. One may wish a more superficial measurement, or one may not have much room for a wide probe with large fiber separations. Diffusion theory fails for such closely spaced fibers.
This report analyzes the generic case of a two-fiber probe spaced less that 1 mm apart. In particular, a widely used commercially available optical fiber probe is considered, which arranges six source fibers around a central collection fiber, where the 400-µm-core-dia. optical fibers are separated by 80 µm (480 µm center-to-center). Its behavior is the same as the generic two-fiber probe. The particular commercial probe design of this report was chosen due to its wide use and reproducible construction, however, the method described in this report can be applied to all such probes. This report will be useful for investigators using spectroscopy for clinical, biomedical, or industrial measurements.
The report considers the probe response when the probe is in contact with a tissue but with near-zero pressure to avoid disturbing the blood perfusion, which is the situation when a local region of a tissue site is being interrogated by a lightly placed probe. Secondly, the non-contact probe response is considered, where the probe is held above the tissue surface yielding a generic diffuse reflectance measurement that is no longer sensitive to the particular inter-fiber spacing of the probe. The results show that the contact probe is not sensitive to the absorption of low-absorption tissues, but sensitive to high absorption and to the scattering properties. The non-contact probe is sensitive to both absorption and scattering, and delivers and collects light from the same spot on the tissue. Therefore lateral diffusion of light allows some light to escape outside this spot and hence escape collection. Such partial collection of light can distort the measured spectra.
A commercial optical fiber probe
Figure 1 shows the face of a commercial multi-fiber probe (400-µm fiber probe, Ocean Insight, Largo, FL, USA) with six source fibers surrounding a single central collection fiber. Monte Carlo simulations were conducted to calculate the delivery and collection of light by the probe. In this report, two conditions were tested: (I) a contact probe, where the probe was assumed to be placed in contact with a tissue, and (II) a non-contact probe, where the probe was held 1 cm above the tissue. The model assumed a homogeneous tissue with uniform absorption and reduced scattering properties. However, the Monte Carlo simulation can be adjusted to model complex tissues, such as a multi-layered tissue like epidermis/dermis or epithelium/stroma. The method reported here can be applied to those simulations. Alternative probe designs with different fiber positions and separations can also be simulated and the method applied.

Methods
Probe in contact with tissue
Monte Carlo simulations of the probe in contact with tissue were conducted. The simulations used mcml.c (18), a cylindrically symmetrical calculation of light transport, to generate point spread functions of escaping flux density at the tissue/probe interface, labeled R(r) (W/cm2 escaping per W delivered) or (cm2), where r denotes the separation between a point source and the position of escape. A range of optical properties were used in 400 simulations: 20 absorption coefficients, µa, logarithmically distributed from 0.01 to 100 (cm-1), and 20 reduced scattering coefficients, µs’ = µs(1-g), logarithmically distributed from 1 to 300 (cm-1). µs is the scattering coefficient and g is the anisotropy equal to the mean value of cos(θ) where θ is the photon deflection angle of a single scattering event, typically g ≈0.90. These ranges are broader than normally found in tissues in order to illustrate the generic behavior of this probe design.
The simulations considered the transport of light from a single source fiber to a single collection fiber. For each µa µs’ pair, the point spread function specified by the simulation was convolved over the face of the source fiber and the light collected over the face of the collection fiber was summed. The result was a single value of collection in units of (W collected/W delivered) or (dimensionless) for a µa,µs’ pair. Because the collected power was normalized by the delivered power, the result for a single two-fiber probe was the same as for a 6-surrounding-1 fiber probe for a homogeneous tissue. Repeating this convolution for all 400 µa,µs’ pairs yielded an analysis grid (i.e., a look-up table) of Rprobe(µa,µs’) (W collected per W delivered) or (dimensionless).
The expected values of µa,µs’ values for a typical soft tissue from 300 to 1,000 nm wavelength was specified by the parameters in Table 1 for the case of a 1% blood content using the following expressions for each wavelength λ:
Full table
[1]
where µa.oxy, µa.deoxy, and µa.water are the absorption spectra of oxygenated hemoglobin, deoxygenated hemoglobin, and water, respectively, from the website https://omlc.org/spectra/. The factor a is the scattering strength [a = µs’(500 nm)], and b is the scattering power. Table 1 lists the other parameters.
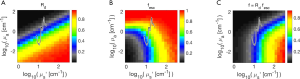
Figure 2A shows the point spread functions calculated by Monte Carlo simulations for escaping flux density as a function of radial position, R(r) (cm-2). Each R(r) curve is for a different pair of absorption (µa) and scattering (µs’) coefficients. The figure shows the location of the source and collection fibers.
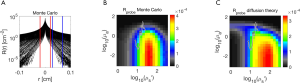
Figure 2B shows a histogram of all distances between source fiber pixels and collection fiber pixels on the faces of the two fibers, based on a 400-µm-dia. fibers. The mean distance is 408 µm.
Figure 2C shows the analysis grid Rprobe(µa,µs’) (dimensionless) based on the Monte Carlo simulations. There is an interval of scattering (x-axis µs’) around 101.56=36 cm-1 in which the strongest probe response occurs. If scattering is too low, the light spreads out in the tissue beyond the collection fibers, so the collected signal drops. If the scattering is too high, the delivered light is prevented from reaching the collection fiber, so again the signal drops. But when the scattering is around 36 cm-1, the scattering is optimal for restricting the light within the tissue around the collection fiber and the collection fibers see a maximum density of escaping flux.
As the absorption initially increases (y-axis µa), there is initially little change in Rprobe because the absorption is so low. The photons scatter to the collector through short pathlengths dominated by the scattering coefficient, so the pathlength [L (cm)] spent by collected photons in the tissue is short. Hence, the attenuation of light, exp(-µaL), is small because photon pathlength L is small. When the absorption becomes stronger (µa >1 cm-1), the probe become more strongly responsive to the tissue’s absorption. In other words, when in contact with a low-absorption tissue, the probe is primarily responsive to the tissue’s scattering properties, which depend on the micron and sub-micron scale of tissue structure. This behavior is due to the close spacing of source and collection fibers. There is always some effect of absorption on the signal due to the background diffuse reflectance involving deeper tissue, but this diffuse signal has spread out beyond the collection fibers and hence is largely not collected.
Figure 2C includes the locus of the µa,µs’ pairs calculated {see Eq. [1]} for a generic tissue with the parameters in Table 1 for the case of a 1% blood content. In other words, this is the reflectance spectrum of the tissue.
Figure 2D shows the analysis grid Rprobe(µa,µs’) based on diffusion theory (18). The general pattern of this grid is similar to the grid generated by Monte Carlo simulations, but there are clear differences that occur in the range of µa,µs’ values typical for tissues. The differences become greater for high absorption and low scattering, which diffusion theory does not adequately model.
The Supplement presents a subroutine Rprobe(µa,µs’) = getRprobe(µa,µs’) that is based on 2D-interpolation of the analysis grid of Figure 2C (Appendix 1).
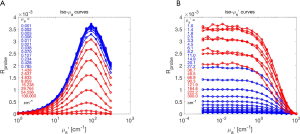
Figure 3 shows the iso-µs’ curves of Rprobe for the range of µa values, and the iso-µs’ curves of Rprobe for the range of µs’ values. The curves show rather slow gradients of change as properties change, which reassures that the 2D interpolation used in getRprobe(µa,µs’) will behave well.
Probe not in contact with tissue
A second analysis grid was also prepared for the probe not in contact with a tissue (Figure 4). The probe was held above the tissue at a height of 1.0 cm and delivered light as a conical beam between ±24.8°. The irradiance was assumed to be uniform over the illuminated spot for this example. A Gaussian-shaped intensity of illumination from the probe source fibers would alter the response a little, because the irradiance would be non-uniform. The flux escaping across the air/tissue boundary (a refractive index mismatch ntissue/nair =1.4) was recorded for each µa,µs’ pair as local diffuse reflectance R(r) (cm-2), and as total diffuse reflectance, Rd (dimensionless).
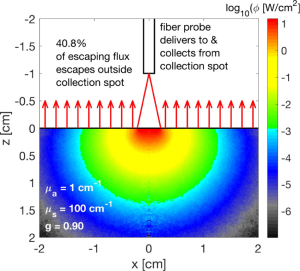
The six source fibers create six spots of illumination, which closely overlap since the inter-fiber spacing is so small compared to the size of the illuminated spots. The central collection fiber collects reflectance from essentially the same spot to which light is delivered. Lateral spread in the tissue causes some of the escaping flux to not be collected. Hence, the probe measures a lower value than the true total diffuse reflectance, Rd. There is also a component of specular reflectance from the tissue surface that is collected by the probe, which does not contain information about the tissue properties.
The following subsection first considers the total diffuse reflectance (Rd) as a function of the optical properties µa,µs’. The second subsection considers the effect of partial collection (fesc) where the probe does not collect the peripheral ring of light that has spread outside the collection spot of the probe.
Total Rd(µa,µs’)
Figure 5A shows the analysis grid Rd(µa,µs’) based on Monte Carlo simulations. As scattering increases, the Rd increases. As absorption increases, Rd decreases. The black line shows the Rd(λ) spectrum expected for a tissue with the properties in Table 1 for the case of 1% blood volume. The spectrum extends from 300–1,000 nm.
Partial collection of Rd(µa,µs’) by non-contact probe
Figure 4 showed the delivery and collection of light by the optical fiber probe to/from a circular spot [radius ≤ h tan(θ), where fiber height h =1 cm]. The simulation was adjusted to deliver an expanding beam of light that illuminated this spot uniformly, which is a simplification to illustrate the effect of partial collection by the cone of light delivered and collected by the probe. The maximum half-angle of delivery/collection was θ =24.8°, which depends on the numerical aperture of the optical fiber. Within the tissue the light spreads and only a fraction (fesc) of the total escaping light (Rd) escapes within this collection spot. A fraction (1-fesc)Rd escapes outside the collection spot. In this example (µa =1 cm-1, µs’ =100 cm-1, g =0.90), only 59.2% of the escaping flux escapes within the collection spot (fesc =0.592). Then only a fraction of this light, fcoll ≈ (πa2)/(2πh2), is collected by the collection fiber of the probe (radius a =200 µm). Therefore, the fraction of total reflectance (Rd) that is collected by the probe is f,
[2]
where fesc =0.592, fcoll =2×10-4, and f = 1.19×10-4 in the example of Figure 4. The factor fesc depends on the tissue optical properties and the spot size of collection.
Figure 5B shows fesc(µa,µs’), illustrating how fesc drops when absorption or scattering become too low and light spreads laterally outside the collection spot. For high absorption or scattering, most of the escaping photons escape within the measurement spot and fesc approaches 1.0.
Figure 5C shows the analysis grid for the product Rdfesc, which is the response for the probe held 1 cm above a tissue. Comparing with Figure 5A, there is significant distortion of the non-contact probe response due to photons at wavelengths of low absorption and low scattering escaping outside the collection spot of the probe.
Results
Using analysis grid to predict probe response: the forward problem
Once the analysis grid has been prepared, it may be used to predict the Rprobe spectrum given particular tissue parameters that determine the optical properties of the tissue over a range of wavelengths. This is called the “forward problem” in which known tissue parameters are used to predict an observed Rprobe spectrum. Given a µa,µs’ pair at each wavelength, the subroutine getRprobe(µa,µs’) yields the expected Rprobe spectrum. This subroutine is listed in the Supplement and is based on the Monte Carlo simulation of the response for the probe in Figure 1 (Appendix 1).
Figure 6 shows the three spectra generated by the µa,µs’ pairs generated by Eq. [2] for each wavelength based on the tissue parameters in Table 1. The spectra are generated by 2D-interpolation of log10(µa),log10(µs’) against the analysis grid. Figure 6A shows the spectra expected when the probe is held in contact with tissue using the Rprobe (µa,µs’) analysis grid.
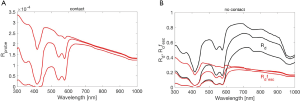
Figure 6B shows the spectra expected when the probe is held 1 cm above the tissue using the Rd(µa,µs’) analysis grid (see getRd() in Appendix 1). The total Rd spectra are shown as black lines. The Rdfesc spectra (red lines) show the reflectance escaping within the collection spot of the fiber probe. The Rdfesc spectra are distorted due to the loss of collected reflectance at wavelengths with low absorption and low scattering because light spreads within the tissue and escapes outside the collection spot. The final term fcoll is ignored in this figure, since it simply scales the spectra by 2×10-4 but does not distort the spectra.
Note that the non-contact Rd(λ) spectra (black lines) show more sensitivity to absorption at long wavelengths than do the contact Rprobe(λ) spectra for the probe in contact with the tissue. The contact probe collects photons that have spent a short pathlength in the tissue, and hence low absorption does not have a chance to exert an effect. In particular, note how the absorption by water in the tissue is seen as a dip in Rd at 960 nm, but is not significant in Rprobe. Also, the slight dip at 760 nm due to deoxy-hemoglobin is seen in Rd but not in Rprobe. However, the Rdfesc spectra (red lines) have lost much of this advantage of sensitivity to low absorption since long-pathlength photons are lost.
Therefore, it is better to deliver light via other fibers (or light sources) illuminating an area much broader that the collection spot so that the problem of partial collection is avoided. Then the collection by the central fiber of the probe will not suffer distortion at wavelengths of low absorption and low scattering. The probe will sample the total reflectance without distortion.
Using analysis grid to analyze probe response: the inverse problem
The “inverse problem” strives to deduce the tissue parameters (Table 1) based on the measured contact-probe spectra Mprobe or the non-contact total reflectance measurement Md, where M indicates the uncalibrated measurement in units of (counts). In this section, Mtissue and Rtissue refer to either Mprobe and getRprobe() or Md and getRd(), depending on whether a contact or non-contact probe is being used. The protocol is listed in two steps:
Take ratio of tissue spectrum to reference spectrum
A reference spectral measurement Mstd(λ) is made by placing the probe above a calibrated reflectance standard, e.g., a SpectralonTM reflectance standard (Rstd =0.99; Labsphere Inc., NH, USA). It is important that the Mstd(λ) is acquired while the probe is not in contact with the reference standard. Otherwise, both the µa(λ) and µs’(λ) of the standard must be known in order to calibrate. A non-contact measurement needs to know only the calibrated Rstd(λ) of the standard reference, which is usually supplied by the manufacturer. The normalized measurement M (dimensionless) for each wavelength is,
[3]
where K = ftissue/fstd. The factor f is the collection efficiency of the measurement on the tissue or reference standard. The geometry of the tissue measurement and the reference measurement need not be the same. For example, a contact measurement has an ftissue that depends on the solid angle of collection by the fiber (Ω) and the fiber collection area (Afiber): ftissue ≈ (Ω/2π)Afiber. The fstd for the reference measurement from some height (h) above the reflectance standard depends on h and Afiber: fstd ≈ Afiber/(2πh2). The tissue measurement may be from a different height than the standard measurement. The factor K is usually an unknown experimental parameter, however it is nearly wavelength-independent and hence scales but does not affect the shape of the spectrum. Eq. [3] is rearranged to place measurements on the left and the least-squares fit on the right,
[4]
Least-squares fitting solves for tissue parameters
Least-squares fitting is applied to match the left and right sides of Eq. [4] to determine B, S, a, b, and K, where a is the scattering strength [a = µs’(λref), e.g., λref =500 nm] and b is the scattering power. The water content W is assigned an assumed value (e.g., W =0.50). The B, S, a, b are used in Eq. [1] to specify Rtissue(λ), and K scales the result. The fitting strives to match the shape of the spectrum, not the absolute value, since the shape is scaled by K.
To illustrate, Figure 7 shows the fitting of two skin spectra taken by (A) the probe in contact with skin, and (B) the non-contact probe. An additional attenuation, exp(-m µa.melaninLepidermis), is included in the analysis to account for the slight amount of melanin in these skin Type II sites (m = melanosome volume fraction in a 60-µm-thick epidermis, Lepidermis is the pathlength spent in the epidermis by escaping photons, which is about three times the epidermal thickness or 180 µm, based on Monte Carlo simulations of skin as increments of melanin are added to the epidermis). The values of B, S, a, b, m and K are shown in Figure 7. This analysis assumes a homogeneous skin with a superficial absorbing filter due to epidermal melanin, and therefore is not as accurate as a multi-layered Monte Carlo simulation of the skin.
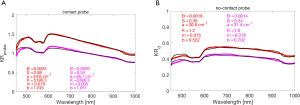
The contact probe shows higher blood content than the non-contact probe, likely due to interrogating the superficial vascular plexus while the non-contact probe also interrogates the reticular dermis with a lower blood content. The contact probe shows a slightly lower scattering strength (a) with a higher scattering power (b), perhaps indicating the difference between scattering in the papillary dermis versus the reticular dermis. The papillary dermis may have smaller collagen fiber bundles than the reticular dermis yielding a smaller scattering strength. The higher b implies a shift toward smaller scale scattering as if the smaller collagen fibrils are not as tightly cross-linked into fiber bundles and are able to behave more like Rayleigh scatterers whose scattering falls more rapidly with wavelength. These conjectures are cited only to suggest how future work could learn about tissue structure from such contact and non-contact probe spectra.
Discussion
This paper is a technical report important for users of optical spectroscopic technology to understand the strengths and weaknesses of a very common type of optical fiber probe that uses two closely spaced fibers. The six-surrounding-one fiber probe in this report will behave the same as a two-fiber probe with one source and one collector, with respect to the variation in signal versus optical properties, although the magnitude of the signal will differ.
The Monte Carlo model in this paper assumed a tissue with homogeneous optical properties. Obviously, this assumption breaks down for complex tissue architectures, such as skin with its multiple layers. However, the model does fit experimental data when the probe is in contact with skin and provides a practical metric for following changes in blood content (B), oxygen saturation (S). For unpigmented tissues, the probe and model can follow changes in B and S. For skin with epidermal melanin, a superficial melanin filter can be included to attenuate the prediction of the homogeneous model (19). The behavior of the probe when held above the skin (non-contact measurement) is illustrated in Figure 7, which cautions about the partial collection of total reflectance that may distort a spectrum.
Conclusions
When an optical fiber probe with closely spaced fibers contacts a tissue (or medium), the response is not sensitive to low absorption values, but is sensitive to µa values above 1 cm-1. The contact probe is sensitive to the scattering properties of the tissue. Therefore, such probes can follow inflammation using the shorter wavelength range and follow structural changes using the longer wavelength range.
When the probe is held above a tissue as a non-contact measurement, the total diffuse reflectance spectrum, Rd(λ), is expected to be sensitive to both absorption and scattering. However, the probe only collects from the spot of illumination, which is specified by the numerical aperture of the fibers and the height of the fiber above the tissue. Consequently, many photons at wavelengths of low absorption and low scattering escape the tissue outside this collection spot, as described by fesc(µa,µs’). The probe collects Rdfesc. Therefore, the non-contact probe loses some of the advantage of Rd for low-absorption sensitivity. If light is delivered more broadly by separate illumination so the non-contact probe samples the central region of a larger illuminated area, then the non-contact measurement will avoid wavelength-dependent losses that distort the spectrum.
Acknowledgments
Funding: None.
Footnote
Provenance and Peer Review: With the arrangement by the Guest Editors and the editorial office, this article has been reviewed by external peers.
Conflicts of Interest: The author has completed the ICMJE uniform disclosure form (available at http://dx.doi.org/10.21037/qims-20-816). The special issue “Advanced Optical Imaging in Biomedicine” was commissioned by the editorial office without any funding or sponsorship. The author has no other conflicts of interest to declare.
Ethical Statement: This paper did not involve a clinical study. The arm spectra of Figure 7 were spectra acquired several years ago at Tufts University under an approved protocol (Prof. Sergio Fantini).
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Liu KZ, Xiang XM, Man A, Sowa MG, Cholakis A, Ghiabi E, Singer DL, Scott DA. In vivo determination of multiple indices of periodontal inflammation by optical spectroscopy. J Periodontal Res 2009;44:117-24. [Crossref] [PubMed]
- Gill AS, Rajneesh KF, Owen CM, Yeh J, Hsu M, Binder DK. Early optical detection of cerebral edema in vivo. J Neurosurg 2011;114:470-7. [Crossref] [PubMed]
- Liasi FT, Samatham R, Jacques SL. Noninvasive in vivo optical characterization of blood flow and oxygen consumption in the superficial plexus of skin. J Biomed Opt 2017;22:1-6. [Crossref] [PubMed]
- Backman V, Wallace MB, Perelman LT, Arendt JT, Gurjar R, Müller MG, Zhang Q, Zonios G, Kline E, McGilligan JA, Shapshay S, Valdez T, Badizadegan K, Crawford JM, Fitzmaurice M, Kabani S, Levin HS, Seiler M, Dasari RR, Itzkan I, Van Dam J, Feld MS. Detection of preinvasive cancer cells. Nature 2000;406:35-6. [Crossref] [PubMed]
- McKenna J, Pabbies A, Friesen JR, Sowa MG, Hayakawa T, Kerr PD. Assessing flap perfusion: optical spectroscopy versus venous doppler ultrasonography. J Otolaryngol Head Neck Surg 2009;38:587-94. [PubMed]
- Farage MA, Cambron T, Liu KZ. Visible-Near Infrared Spectroscopic Assessment of Urogenital Tissue in Premenopausal and Postmenopausal Women. Clin Med Insights Womens Health 2018;11:1179562X17749608.
- Dhar A, Johnson KS, Novelli MR, Bown SG, Bigio IJ, Lovat LB, Bloom SL. Elastic scattering spectroscopy for the diagnosis of colonic lesions: initial results of a novel optical biopsy technique. Gastrointest Endosc 2006;63:257-61. [Crossref] [PubMed]
- Lin WC, Toms SA, Johnson M, Jansen ED, Mahadevan-Jansen A. In vivo brain tumor demarcation using optical spectroscopy. Photochem Photobiol 2001;73:396-402. [Crossref] [PubMed]
- Villringer A, Chance B. Non-invasive optical spectroscopy and imaging of human brain function. Trends Neurosci 1997;20:435-42. [Crossref] [PubMed]
- Shah N, Cerussi AE, Jakubowski D, Hsiang D, Butler J, Tromberg BJ. The role of diffuse optical spectroscopy in the clinical management of breast cancer. Dis Markers 2003-2004;19:95-105. [Crossref] [PubMed]
- Bensalah K, Peswani D, Tuncel A, Raman JD, Zeltser I, Liu H, Cadeddu J. Optical reflectance spectroscopy to differentiate benign from malignant renal tumors at surgery. Urology 2009;73:178-81. [Crossref] [PubMed]
- Nilsson JH, Reistad N, Brange H, Öberg CF, Sturesson C. Diffuse Reflectance Spectroscopy for Surface Measurement of Liver Pathology. Eur Surg Res 2017;58:40-50. [Crossref] [PubMed]
- Aerts JG, Amelink A, van der Leest C, Hegmans JP, Hemmes A, den Hamer B, Sterenborg HC, Hoogsteden HC, Lambrecht BN. HIF1a expression in bronchial biopsies correlates with tumor microvascular saturation determined using optical spectroscopy. Lung Cancer 2007;57:317-21. [Crossref] [PubMed]
- Mourant JR, Bigio IJ, Boyer J, Conn RL, Johnson T, Shimada T. Spectroscopic diagnosis of bladder cancer with elastic light scattering. Lasers Surg Med 1995;17:350-7. [Crossref] [PubMed]
- Bigio IJ, Mourant JR. Ultraviolet and visible spectroscopies for tissue diagnostics: fluorescence spectroscopy and elastic-scattering spectroscopy. Phys Med Biol 1997;42:803-14. [Crossref] [PubMed]
- Rodriguez-Diaz E, Castanon DA, Singh SK, Bigio IJ. Spectral classifier design with ensemble classifiers and misclassification-rejection: application to elastic-scattering spectroscopy for detection of colonic neoplasia. J Biomed Opt 2011;16:067009. [Crossref] [PubMed]
- Wang L, Jacques SL, Zheng L. MCML--Monte Carlo modeling of light transport in multi-layered tissues. Comput Methods Programs Biomed 1995;47:131-46. [Crossref] [PubMed]
- Farrell TJ, Patterson MS, Wilson B. A diffusion theory model of spatially resolved, steady-state diffuse reflectance for the noninvasive determination of tissue optical properties in vivo. Med Phys 1992;19:879-88. [Crossref] [PubMed]
- Jacques SL, Samatham R, Choudhury N. Rapid spectral analysis for spectral imaging. Biomed Opt Express 2010;1:157-64. [Crossref] [PubMed]


