
A transmission measurement-based spectrum estimation method incorporating X-ray tube voltage fluctuation
Introduction
The X-ray energy spectrum, which displays the relative fraction of photons at different energies during an exposure, is a fundamental distinctive feature of the X-ray tube. It has a direct or indirect impact on correction for beam-hardening artifacts, Monte Carlo (MC) simulation, and others. For example, MC simulation (1,2), which is regarded as the gold standard in the field of particle transport, utilizes the source energy spectrum and its fluence map to initialize the photons of the source. However, the gold standard will no longer exist if the physical data loaded at the beginning are inaccurate.
For obtaining the energy spectrum of the X-ray imaging system, various methods have been proposed. Due to the limited count rate of the spectrum detector, it is difficult to measure the spectrum directly. Most of the methods are indirect, which are approximately classified into four categories: Compton-scattering measurement, MC simulation, spectra modeling, and transmission measurements. For compton-scattering measurement (3,4), the spectrum is calculated using the scattered spectrum and the corresponding scattering angle. The scattered spectrum can be generated via measuring the Compton-scattering photons directly. System calibration is complicated due to the absorption in the scatterer and the limited absorption efficiency of the detector. Most of the MC packages (5,6) provide comprehensive physics modeling and are well validated. However, in addition to the energy spectrum, there are other factors that influence the simulation results. Spectra modeling methods (7,8) usually adopt an empirical or semi-empirical approach that fits a parameterized model based on physical processes. Transmission measurements (9,10) estimate the spectrum using projections of a calibration phantom which requires dedicated hardware or workflow. In order to avoid such drawbacks, an indirect transmission measurement-based spectrum estimation method (11) was proposed, which expresses the estimated X-ray spectrum as the weighted summation of a set of model spectra. In this method (11), each model spectrum is the spectrum that the X-rays penetrate with a filter of a certain thickness and voltage. Then, an estimated projection can be computed via the ray-tracing method using the estimated spectrum. The final spectrum is calculated with these calibrated weights which minimize the difference between the reprojection and the raw projection. The method does not need any special phantom or high-precision measuring tools and can reduce the complexity of solving.
However, the method introduced above has a drawback in that it does not take the voltage fluctuation (12,13) into consideration. It only utilizes the model spectra at a preset voltage, and we therefore refer to it as the single-voltage method. In reality, it is difficult to generate an ideal voltage. The X-ray tube will not stabilize at a voltage during the entire exposure and will instead fluctuate around the preset voltage (14). There will be a process of rising, oscillating, and falling (15). The amplitude of the fluctuation is related to the quality of the machine and the X-ray tube. Different from the single-voltage method, we take the voltage fluctuation into account to estimate the spectrum as accurately as possible. Specifically, the model spectra that cover a voltage range are utilized to estimate the real spectrum of the X-ray tube, which expands the voltage range of the model spectra. For the sake of simplicity, we refer to the method proposed in this study the poly-voltage method.
Methods
Figure 1 shows the proposed workflow of the poly-voltage method. The first step is to acquire the raw projection data exposed by the X-ray tube. A modified Feldkamp-Davis-Kress (FDK) algorithm (16), one of the classical analytic reconstruction methods, integrated with geometric calibration results (17), is used to reconstruct a three-dimensional (3D) image. The second step is to load the reconstructed image and the initial estimated spectrum into the ray-tracing algorithm for calculating the estimated projection, a process referred to as reprojection. In order to minimize the difference between the raw projection and the reprojection, we set the difference as the objective function, and it is optimized for iteratively updating the weights of the model spectra. Finally, the best estimated spectrum is calculated with the model spectra and the corresponding weight.
In the poly-voltage method, we take the voltage fluctuation into account. The model spectra are produced from various voltages, and the spectrum can be represented as the weighted sum of the model spectra as follows:
Here, Sreal is the real spectrum produced by the X-ray tube during exposure; M is the number of voltages, which represents the voltage range of the model spectra; N is the number of model spectra at each voltage, which represents different thicknesses of the filter; Sij is the model spectrum at ith voltage with jth thickness of the filter; and wij is the weight of Sij. At the beginning, the initial estimated spectrum can be calculated with the weights set randomly, and the weights are updated with an iterative optimization algorithm.
Voltage fluctuation
From the technical standard (18,19), we know that the deviation of the tube voltage should not exceed ±10% or ±10 kV. In addition, according to the relevant literature (20,21) and the tube voltage pulse measured in our in-house cone-beam computed tomography (CBCT) system, we can know that the phenomenon of voltage fluctuation is real. In an ideal situation, the exposure voltage will remain stable at the preset value during the entire exposure, and the voltage will increase and decrease very quickly at the beginning and end of the exposure, respectively. Focusing on the tube voltage pulse measured in our in-house CBCT system, we can observe that the tube voltage will rise to a value that is higher than the preset value at first and then gradually decrease to the preset value. The difference between the ideal voltage pulse and the real voltage pulse can be clearly seen in Figure 2. Of the pulses shown in Figure 2, the first pulse is obtained by fitting the actually measured pulse. For convenience, the second value is copied from the first. Based on the above phenomenon, a single real exposure can be interpreted as many short exposures at different voltages. In other words, the actual spectrum of the X-ray tube can be expressed as the weighted summation of numbers of model spectra from different voltages.
The model spectra used in the single-voltage method are generated at the preset voltage with different thicknesses of the filter. The high-energy photon that exceeds the preset voltage will not be simulated, and the estimated spectrum does not match the real spectrum well. Therefore, we propose the poly-voltage method to cover a wide voltage range of the model spectra.
Model spectra
There are a variety of ways to generate model spectra, such as the MC simulation (5,22,23) and SPEKTR 3.0 software (24). In our work, we generate model spectra using SPEKTR3.0 software, which was developed to calculate X-ray spectra using the TASMICS (tungsten anode spectral model using interpolating cubic splines) algorithm (25) based on the TASMIP (tungsten anode spectral model using interpolating polynomials) spectral model (26). As for the process of generating model spectra in the spectrum estimated method, the tube voltage, material type, and thickness of the filter need to be defined. The tube voltage is included in a certain range in the “Model spectra mixture evaluation” section. The model spectra are filtered with 3, 4, 6, 8, 10, 12, and 18 mm of aluminum at each voltage, respectively. If one can use a broad range of the thicknesses of the filter, and sample more intensively, the accuracy of the estimated spectrum will improve; however, the calibration time may also increase. The requirement of the model spectra is that the softest model spectrum should be softer than the true spectrum while the hardest model spectrum should be harder than the true spectrum. For simplicity, we used the filter thickness (3, 4, 6, 8, 10, 12, 18 mm) from the reference which can obtain an acceptable spectrum.
Ray-tracing algorithm
After phantom image reconstruction, the ray-tracing algorithm is used to obtain the reprojection. The ray-tracing algorithm is based on Beer-Lambert law (27). It is expressed in Eq. [2]:
where I and I0 are the incident and transmitted X-ray intensities, L is the length of the X-ray through the phantom, and µ is the linear attenuation coefficient of the material, which is a function of the incident X-ray photon energy. In Eq. [2], the X-ray beam is single energy and the phantom is composed of a single homogeneous material, which is inconsistent with reality. In reality, X-rays are multienergy, and a phantom is composed of a variety of materials. We therefore apply Beer-Lambert law as in Eq. [3]:
where Ii is the normalized flux of the ith energy segment, µij is the linear attenuation coefficient of the photon in the ith energy segment when passing through the jth voxel, and Lj is the length that the X-ray penetrates the jth voxel. For implementing Eq. [3], Siddon’s algorithm (28,29) is firstly used to calculate the length of each X-ray passing through each voxel. The attenuation coefficients of the different energy rays in each voxel are from the table of the National Institute of Standards and Technology (NIST) database (30). Finally, the reprojection is calculated via Eq. [3].
Updating weights
To make the reprojection match the raw projection well, we optimize the weights of the model spectra constantly until a preset number of iterations has been completed. Prior to this study, we compared particle swarm optimization (PSO) (31,32), genetic algorithm (GA) (33,34), and the equilibrium optimizer (EO) (35-37) algorithm. We found that EO yielded the best results based on the stability of the solution and iteration speed. Therefore, we used EO in this study. EO is inspired by the control volume mass balance model for estimating both dynamic and equilibrium states. In EO, the concentration of each particle is a solution, and the change in concentration of each particle acts as a search agent. The search agents update the concentration randomly from the best-so-far solutions, namely equilibrium candidates, and reach the equilibrium state as the optimal result. In order to keep the solution physically meaningful, a nonnegative constraint is applied to the weights. In this study, we execute EO in MATLAB (MathWorks, Natick, MA, USA). The pseudocode is presented below and can be briefly summarized as follows.
First, we initialize the number of independent runs Rn=1; the number of random number Pn=25, the maximum number of iterations Mi=360, and the number of weight Wd is equal to the number of model spectra. Then, line 2 of the pseudocode initializes the weight combination set C, and each weight value is in the interval [lb, ub], lb=0 and ub=1. From lines 3 to 7, we obtain the optimal four groups (Ceq1, Ceq2, Ceq3, Ceq4) from the weight combination set (C) according to fitness. The fitness fit(C(i, :)) at line 5 represents the difference of the middle row profiles between the estimated projection (p_est) and the raw projection (p_raw) for the ith weight combination. The specific expression is shown in line 5 and is equal to the sum of the absolute values of the difference. We build the equilibrium pool (Ceq_pool) with Ceq1, Ceq2, Ceq3, Ceq4, and Ceq_aveat line 9. Ceq_ave is the arithmetic mean of the mentioned four particles. Finally, line 12 generates the new weight combination set (C) according to the equilibrium pool (Ceq_pool). See Faramarzi et al. (35) for the specific generating process.
Line 1: Initialize Rn, Pn, Mi, Wd;
Line 2: Calculate C = rand(Pn, Wd) × (ub − lb) + lb;
Line 3: While iteration < Mi;
Line 4: For i=1:Pn;
Line 5: Fit(C(i, :)) = sum(abs(p_est - p_raw));
Line 6: Update Ceq1, Ceq2, Ceq3, Ceq4;
Line 7: End;
Line 8: Ceq_ave = (Ceq1 + Ceq2 + Ceq3 + Ceq4)/4;
Line 9: Ceq_pool = {Ceq1, Ceq2, Ceq3, Ceq4, Ceq_ave};
Line 10: For i=1:Pn;
Line 11: Ceq = Ceq_pool {rand(size(Ceq_pool, 1), 1)};
Line 12: Generate the new weight combination set C;
Line 13: End;
Line 14: Iteration = iteration + 1;
Line 15: End while.
Experiments and evaluation
In this section, we described how the model spectra mixture evaluation and projection evaluation verified the correctness of the poly-voltage method and identified the voltage range of the model spectrum. The aim of using phantom evaluation was to not only prove that the poly-voltage method not only provides accurate reprojection, but can also the accurately estimate the spectrum. The aim of the scatter evaluation was to assess the difference between the estimated scatter signals using the estimated spectrum via the two methods and to determine whether it is necessary to load the spectra via the poly-voltage method in MC simulation for scatter simulation.
Model spectra mixture evaluation
In this evaluation, three modes of X-ray tube voltage pulse including the ideal pulse mode, long pulse mode, and short pulse mode were used to highlight the difference among the spectra estimated by the different methods. As shown in Figure 3, the ideal pulse mode was set to 90 kV during the whole exposure, and the other two were the same as the real voltage pulse. Both the preset voltage of the long and the short pulse mode were 90 kV. The former slightly oscillated around 93 kV, whereas the latter slightly oscillated around 90 kV. In this evaluation, the reference spectrum was composed of the model spectra filtered with 10 mm of aluminum.
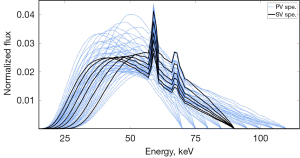
Voltage range refers to the voltage range covered by the model spectra. For instance, we set 90 kV as the exposure voltage and 10% as the voltage range. This means that the voltage of the model spectra covered from 81 to 99 kV. Figure 4 shows a sample of the model spectra in the poly-voltage method and single-voltage method. One line in the figure indicates as one model spectrum, and the model spectra which have the same end point are generated at the same voltage. For the model spectra, there were 6 model spectra at 1 voltage, which were filtered with 3, 4, 6, 8, 12, and 18 mm of aluminum, respectively. The number of model spectra used in the poly-voltage method was larger than that in the single-voltage method. Moreover, the voltage range was sufficiently wide to cover the peak of the voltage pulse.
Projection evaluation
To verify the difference between two reprojections obtained via the two methods, a 3D phantom image of a pelvis was used in the ray-tracing algorithm. The phantom matrix and the size of the voxel were 512×512×70 and 0.1172×0.1172×0.3 cm3, respectively. The source to axis of rotation distance (SAD) and axis of rotation to image distance (AID) were set to 100 and 50 cm, respectively. Then, we generated reprojections via the ray-tracing algorithm and compared the difference between the generated projections.
Phantom evaluation
A digital phantom simulation and a polymethyl methacrylate (PMMA) phantom experiment were performed. A digital cylindrical water phantom was used in the numerical simulation. The phantom matrix was 780×780×620, and the size of voxel was 0.2×0.2×0.2 cm3. The reference projection is the reprojection of the phantom via the ray-tracing algorithm using the reference spectrum, which is combined with model spectra with consideration to the measured voltage fluctuation. We executed the PMMA phantom experiment with a 6-degrees of freedom (DoF) robot-based in-house CBCT system as shown in Figure 5A. In this configuration, there were two robotic manipulators upon which the X-ray tube and the detector were respectively mounted. The optional voltage range was from 40 to 140 kV, and the optional tube current range was from 10 to 120 mA. The detector resolution was 1,920×1,536 with a physical size of 24.4×19.5 cm2. The PMMA phantom consisted of an upper cone and a lower cylinder, as shown in Figure 5B. The height of the cone and the cylinder were both 90 mm, and the diameter of the bottom of the cone was 140 mm, equal to the diameter of the cylinder. The raw projections were obtained from the 6-DoF robot-based in-house CBCT system. The SAD and AID were 100 and 50 cm, respectively. A total of 360 projections were equally acquired in 360 degrees with the tube voltage of 85 kV. In order to minimize the impact of scattering, the scanner was equipped with a narrow collimator. Therefore, the contribution of the scatter signal to the raw projections could be neglected. The 3D image was reconstructed via the FDK algorithm. Then, we calculated the two spectra estimated via the poly-voltage method and single-voltage method according to the workflow presented in Figure 1. The resulting spectra were utilized for beam-hardening artifact correction (38-41). The artifacts could be corrected using the water correction method, which transforms the total attenuation values from polychromatic to monochromatic using polynomial-based nonlinear mapping.

Scatter evaluation
In this evaluation, the MC simulations of CBCT projections were developed using the GPU-based MC package (gMCDRR) by Jia et al. (42). In gMCDRR, the detector can collect and distinguish the primary signal and the scatter signal. Multiple GPU threads are launched to transport photons simultaneously. Each photon is transported from the X-ray source until it exits the phantom or is absorbed in the phantom. Within each thread, the state of the X-ray source photon is initialized by the energy spectrum and fluence. The source photon energy must be generated according to the spectrum. As for the fluence, it is used to specify the probability density of a photon traveling toward the detector after emission from the source. If a photon exits from the phantom, its energy is recorded at a corresponding detector pixel in either the primary counter or the scatter counter depending on whether a scattering event has occurred. In this study, we used a digital water phantom and the gMCDRR to simulate the scatter signals with two estimated spectra calculated in the PMMA phantom experiment. The phantom matrix was 128×128×96, and the voxel size was 0.1×0.15×0.15 cm3. The detector resolution was 512×384 with size of 40×30 cm2. The SAD and AID were set as 100 and 50 cm, respectively. The total number of photons we simulated in gMCDRR was 2×1012.
Performance comparison
In the model spectra mixture evaluation, for quantitative comparisons, absolute error and percentage error of each energy bin were calculated to show the difference between the reference spectrum and the estimated spectrum. Furthermore, the mean energy difference (MED) and normalized root mean square error (NRMSE) were used to evaluate the effect of the voltage range on the accuracy of the estimated spectrum. MED and NRMSE can be defined as follows:
where Se(n) is the normalized flux of bin n in the estimated spectrum, Sref(n) is the normalized flux of bin n in the reference spectrum, En is the photon energy of bin n, and N is the total bin number of the spectrum. In the projection evaluation, profiles of the projections and the percentage error graph were compared in a quantitative analysis. In the phantom evaluation, beam-hardening artifacts appeared as cupping artifacts on reconstructed images of the PMMA and water phantom. The image appeared dark in the middle and light in the periphery. With the profile of the middle row of the image, a concave curve appeared with the two sides high and the middle low. The deeper the concave curve was, the more serious the artifact. We determined the severity of artifacts qualitatively by observing the degree of sag of the profile (i.e., flatness). The spectra generated by the two methods were used to perform beam-hardening correction on the projection, and the severity of cupping artifacts in the two reconstructed images were compared qualitatively to verify which method is more accurate. We also calculated the NRMSE of the middle row profile between the estimated projection and the reference projection, as well as the NRMSE indices between the estimated spectrum and the reference spectrum. The accuracy of the estimated spectrum from the two methods and the deviation of the reprojection were then compared using the NRMSE index. In scatter evaluation, we compared the profiles of the scatter signals generated using two spectra directly, and the percentage error was used as the quantification index of the difference.
Results
Model spectra mixture evaluation
Figure 6A-6C show the estimated spectra generated via the poly-voltage method and single-voltage method of the X-ray tube in ideal pulse mode, long pulse mode, and short pulse mode, respectively. Figure 6A shows that both methods could estimate the reference spectrum quite well with an ideal voltage; indeed, in a comparison with Figure 6B,6C, it appears that the voltage variation does have an impact on the results of the single-voltage method, whereas the poly-voltage method can match the reference spectrum well whether the voltage pulse is ideal or not. Figure 6D-6F show the difference in terms of absolute error and percentage error. Generally, the flux of spectrum estimated via the single-voltage method was higher than the reference spectrum before the characteristic radiation and lower at higher energies.
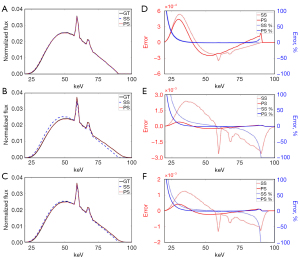
Figure 7 shows the MED (Figure 7A) and NRMSE (Figure 7B) of the estimated spectrum generated via the poly-voltage method with different voltage ranges. In the figure, the horizontal coordinate is the voltage range. The arrows in figures indicate the highest peak of the voltage pulse. With the expansion of voltage range, the MED and NRMSE between the estimated spectrum and reference spectrum gradually approach a constant. The mean and fluctuation range of each index in the stable stage are shown in Table 1. The voltage range that the arrow indicates can be used as the voltage range of the model spectra.
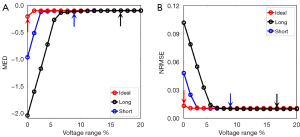
Table 1
| Tube mode | MED | NRMSE | |||
|---|---|---|---|---|---|
| Mean | Range | Mean | Range | ||
| Ideal pulse | −1.01×10−1 | ±0.49% | 1.08×10−2 | ±0.04% | |
| Long pulse | −1.03×10−1 | ±4.53% | 1.00×10−2 | ±0.42% | |
| Short pulse | −9.91×10−2 | ±3.36% | 1.03×10−2 | ±1.01% | |
Mean, mean value; range, the maximum fluctuation value away from the mean. MED, mean energy difference; NRMSE, normalized root mean square error.
Projection evaluation
Figure 8 shows the projections generated via the poly-voltage method and single-voltage method in the ideal pulse mode, long pulse mode, and short pulse mode. In the figure, the ground truth (GT) refers to the reference projections produced via the ray-tracing algorithm using the reference spectra. The arrows indicate the visible difference between the reprojections and the reference projection among the same pulse mode. Profile comparisons for the ideal pulse mode of the reference projection and reprojections are shown in Figure 9A. The percentage error of the reprojections generated via the single-voltage method and poly-voltage method are shown in Figure 9. Figure 9D-9F present the long pulse mode, and Figure 9G-9I present the short pulse mode. The maximum percentage error of the reprojections generated via the two methods in three pulse modes are shown in Table 2. In the table, the error of the reprojection generated via the single-voltage method is larger when the tube voltage has more fluctuation, demonstrating that the poly-voltage method can calculate a more accurate and stable spectrum.

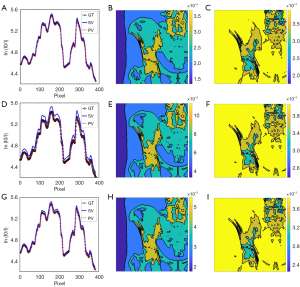
Table 2
| Methods | Ideal pulse | Long pulse | Short pulse |
|---|---|---|---|
| Single-voltage | 4.27% | 13.33% | 6.41% |
| Poly-voltage | 0.44% | 0.42% | 0.45% |
Phantom evaluation
Digital phantom simulation
Figure 10 shows the results of the digital phantom simulation in the phantom evaluation. Figure 10A presents the reference spectrum and two estimated spectra generated via the two methods. In the figure, the estimated spectrum generated via the poly-voltage method is more accurate than that generated via the single-voltage method. The NRMSE of the estimated spectrum generated via the single-voltage method was 14.95%, whereas that generated via the poly-voltage method was 2.66%. The profile comparison is shown in Figure 10B. In the comparison of the reprojections, the NRMSE generated via the poly-voltage method was 0.0352%, whereas that generated via the single-voltage method was 0.1258%. Figure 10C shows the error of profile between the reprojections and the reference projection. The reprojection generated via the poly-voltage method was slightly more accurate than that generated via the single-voltage method. The reason for this is that the reprojection calculated by the ray-tracing algorithm is the result of integration. In comparing the spectrum obtained via the single-voltage method with the reference spectrum, it can been that the photon in the low-energy part is more and that in the high-energy part is less. In the forward projection, the missing integral of the high-energy part is compensated by the low-energy part. Even though the two spectra are quite different, the reprojection generated via the single-voltage method can match the reference projection well.
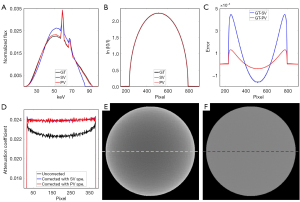
For the performance of beam-hardening correction, profiles of the uncorrected images and the corrected images using spectra that generated via the single-voltage method and poly-voltage method are shown in Figure 10D. The profiles of correction produced using the estimated spectra generated via the two methods are visually flat and similar. Therefore, we only present the image without correction in Figure 10E and the image corrected with the spectrum generated via the poly-voltage method in Figure 10F. The image without correction in Figure 10E has severe beam-hardening artifacts, while Figure 10F shows that the artifacts almost disappeared after correction, demonstrating the accuracy of the estimated spectrum.
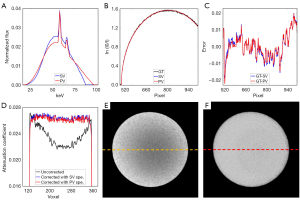
PMMA phantom experiment
Figure 11 shows the results of the PMMA phantom experiment in our robot-based in-house CBCT system. Figure 11A shows two estimated spectra generated via the 2 methods. Profiles of the raw projection and reprojections are shown in Figure 11B, and profile errors between the raw projection and reprojection are shown in Figure 11C. The NRMSE profile of the reprojection generated via the poly-voltage method was 0.7573%, whereas that generated via the single-voltage method was 0.8002%. The NRMSE in the realistic experiment was larger than that of the simulation study due to various external factors, such as scattering. Figure 11D shows the profiles of the center column of Figure 11E,11F. Figure 11E,11F are the results without correction and correction with the spectrum generated via the poly-voltage method, respectively. The beam-hardening artifacts almost disappeared after correction.
Scatter evaluation
Figure 12A shows the profiles of scatter signals using the spectra generated in the PMMA phantom experiment. Figure 12B shows the estimated scatter using the spectra generated by the poly-voltage method, and Figure 12C shows the estimated scatter using the spectra generated by the single-voltage method. The percentage error was 1.77%. The comparison of the results using the spectra obtained via the single-voltage method and poly-voltage method showed little difference. The reason for this is that the low-energy part of the spectrum generated with the single-voltage method was more than that generated with the poly-voltage method, but the high-energy part generated with the single-voltage method was less than that generated with the poly-voltage method. Thus, the reason explained above plays a neutralizing role when generating the scatter.

Discussion
We developed an indirect spectrum estimation method that incorporates the voltage fluctuation of the X-ray tube. The estimated spectrum is expressed as the weighted summation of a set of model spectra as generated using SPEKTR3.0 software (24). The method mentioned by Zhao et al. (11) only simulates the spectrum at 1 voltage with different thicknesses of the filter, which does account for the realistic voltage pulse oscillation during exposure. We referred to this as the single-voltage method and compared it with the poly-voltage method. The method mentioned by Sidky et al. (9) decomposes the spectrum into a number of energy bins using a set of basis functions. This method is intuitive but introduces too many unknown variables (equal to the number of energy bins), making the inverse problem highly underdetermined, and it cannot recover fine details of the spectrum without proper initialization. The single-voltage method and the poly-voltage method can significantly reduce the DoF.
From the model spectra mixture evaluation, the single-voltage method cannot simulate part of the high-energy photons in the reference spectrum. The spectrum obtained via the single-voltage method is narrower than the reference spectrum, whereas that obtained via the poly-voltage method can match the reference spectrum well. It is difficult to obtain the actual voltage pulse in realistic applications. According to previous reports (20,21) and the tube voltage pulse measured in our in-house CBCT system, we recommend the maximum voltage fluctuation range to be 10% and regard it as the voltage range of the model spectra. According to the phantom evaluation, both reprojections via the two methods can match the raw projection well, with the one that uses the spectrum generated via poly voltage being just slightly better than that generated via single voltage, even though the spectrum generated via the single-voltage method is quite different from the reference spectrum. The reason for this that when we use an energy-integrating detector, the missing contribution to the reprojection of the high-energy photons can be compensated with the low-energy photons. The single-voltage method aims to make the raw projection and the reprojection as similar as possible but ignores the distribution of the particles with different energies in the energy spectrum. The poly-voltage method takes both into consideration, so the spectrum generated via the poly-voltage method matches the reference spectrum better than does that generated with the single-voltage method. However, there are many interference factors in realistic applications, which renders the fitness of the projection in the realistic experiment inferior to the numerical simulation.
According to above evaluations, the NRMSE index between the spectrum via the poly-voltage method and the reference spectrum should be kept within 3% under different mode voltages. The best result of the single-voltage method reported is 4% (11). However, the NRMSE index of the estimated spectrum under different mode voltages may have a large deviation. We also compared the scatter signals using estimated spectra and gMCDRR. There was a slight difference between the estimated scatter signals. Therefore, the poly-voltage method can be considered for the scatter simulation.
More experiments need to be designed for evaluating the accuracy of the poly-voltage method. In a field that requires the precise distribution of photons during exposure, such as multienergy computed tomography, the poly-voltage method may have considerable value. In the future, if we aim to estimate a more accurate spectrum using the poly-voltage method in realistic applications, any influencing factors need to be considered as much as possible when obtaining raw projections.
Conclusions
We propose an X-ray energy spectrum estimation method called the poly-voltage method. It expresses the real spectrum as the weighted summation of a set of model spectra at a voltage range, which considers the voltage fluctuation of the X-ray tube. The results of evaluations demonstrate that the spectrum can be accurately estimated from different voltage pulses via the proposed method.
Acknowledgments
Funding: This work was supported by the National Natural Science Foundation of China (Nos. 61971463, 82272131, and 82202960), the Ministry of Science and Technology Planning Project of Guangdong (No. 2023A1515010537), and the National Key R&D Program of China (No. 2019YFC0121901).
Footnote
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at https://qims.amegroups.com/article/view/10.21037/qims-22-1055/coif). The authors have no conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Jia X, Gu X, Graves YJ, Folkerts M, Jiang SB. GPU-based fast Monte Carlo simulation for radiotherapy dose calculation. Phys Med Biol 2011;56:7017-31. [Crossref] [PubMed]
- Jia X, Yan H, Gu X, Jiang SB. Fast Monte Carlo simulation for patient-specific CT/CBCT imaging dose calculation. Phys Med Biol 2012;57:577-90. [Crossref] [PubMed]
- Yaffe M, Taylor KW, Johns HE. Spectroscopy of diagnostic x rays by a Compton-scatter method. Med Phys 1976;3:328-34. [Crossref] [PubMed]
- Maeda K, Matsumoto M, Taniguchi A. Compton-scattering measurement of diagnostic x-ray spectrum using high-resolution Schottky CdTe detector. Med Phys 2005;32:1542-7. [Crossref] [PubMed]
- Ay MR, Shahriari M, Sarkar S, Adib M, Zaidi H. Monte carlo simulation of x-ray spectra in diagnostic radiology and mammography using MCNP4C. Phys Med Biol 2004;49:4897-917. [Crossref] [PubMed]
- Darvish-Molla S, Spurway A, Sattarivand M. Comprehensive characterization of ExacTrac stereoscopic image guidance system using Monte Carlo and Spektr simulations. Phys Med Biol 2020;65:245029. [Crossref] [PubMed]
- Birch R, Marshall M. Computation of bremsstrahlung X-ray spectra and comparison with spectra measured with a Ge(Li) detector. Phys Med Biol 1979;24:505-17. [Crossref] [PubMed]
- Tucker DM, Barnes GT, Chakraborty DP. Semiempirical model for generating tungsten target x-ray spectra. Med Phys 1991;18:211-8. [Crossref] [PubMed]
- Sidky EY, Yu L, Pan X, Zou Y, Vannier M. A robust method of x-ray source spectrum estimation from transmission measurements: Demonstrated on computer simulated, scatter-free transmission data. J Appl Phys 2005;97:124701. [Crossref]
- Duan X, Wang J, Yu L, Leng S, McCollough CH. CT scanner x-ray spectrum estimation from transmission measurements. Med Phys 2011;38:993-7. [Crossref] [PubMed]
- Zhao W, Niu K, Schafer S, Royalty K. An indirect transmission measurement-based spectrum estimation method for computed tomography. Phys Med Biol 2015;60:339-57. [Crossref] [PubMed]
- Matsumoto M, Kubota H, Hayashi H, Kanamori H. Effects of voltage ripple and current mode on diagnostic x-ray spectra and exposures. Med Phys 1991;18:921-7. [Crossref] [PubMed]
- Matsumoto M, Kubota H, Ozaki Y, Kanamori H. Experimental verification of reverse order of diagnostic X-ray beam quality in voltage-ripple dependence. Med Biol Eng Comput 1995;33:48-51. [Crossref] [PubMed]
- Kramer HM, Selbach HJ, Iles WJ. The practical peak voltage of diagnostic X-ray generators. Br J Radiol 1998;71:200-9. [Crossref] [PubMed]
- Chida K, Saito H, Ito D, Shimura H, Zuguchi M, Takai Y. FFT analysis of the X-ray tube voltage waveforms of high-frequency generators for radiographic systems. Acta Radiol 2005;46:810-4. [Crossref] [PubMed]
- Wiesent K, Barth K, Navab N, Durlak P, Brunner T, Schuetz O, Seissler W. Enhanced 3-D-reconstruction algorithm for C-arm systems suitable for interventional procedures. IEEE Trans Med Imaging 2000;19:391-403. [Crossref] [PubMed]
- Duan XM, Cai JZ, Ling QQ, Huang YC, Qi HL, Chen YS, Zhou LH, Xu Y. Knowledge-based self-calibration method of calibration phantom by and for accurate robot-based CT imaging systems. Knowledge-Based Systems 2021;229:107343. [Crossref]
- Administration SD. Medical electrical equipment-Part 2: Particular requirements for the safety of high-voltage generators of diagnostic X-ray generators. State Bureau of Quality Technical Supervision, 2000. Available online: https://www.antpedia.com/standard/435667-1.html
- Commission IE. Medical electrical equipment-Part 2-54: Particular requirements for the basic safety and essential performance of X-ray equipment for radiography and radioscopy. 2018. Available online: https://webstore.ansi.org/standards/iec/iec6060154ed2018
- Strauss KJ. Interventional suite and equipment management: cradle to grave. Pediatr Radiol 2006;36:221-36. [Crossref] [PubMed]
- Hourdakis CJ. Determination of the diagnostic x-ray tube practical peak voltage (PPV) from average or average peak voltage measurements. Phys Med Biol 2011;56:2199-217. [Crossref] [PubMed]
- Bazalova M, Verhaegen F. Monte Carlo simulation of a computed tomography x-ray tube. Phys Med Biol 2007;52:5945-55. [Crossref] [PubMed]
- Chadeeva M, Korpachev S. Validation of Geant4 Simulation and Digitization of a SiPM-on-Tile System. Physics of Atomic Nuclei 2021;84:585-9. [Crossref]
- Siewerdsen JH, Waese AM, Moseley DJ, Richard S, Jaffray DA. Spektr: a computational tool for x-ray spectral analysis and imaging system optimization. Med Phys 2004;31:3057-67. [Crossref] [PubMed]
- Hernandez AM, Boone JM. Tungsten anode spectral model using interpolating cubic splines: unfiltered x-ray spectra from 20 kV to 640 kV. Med Phys 2014;41:042101. [Crossref] [PubMed]
- Boone JM, Seibert JA. An accurate method for computer-generating tungsten anode x-ray spectra from 30 to 140 kV. Med Phys 1997;24:1661-70. [Crossref] [PubMed]
- Mamouei M, Budidha K, Baishya N, Qassem M, Kyriacou PA. An empirical investigation of deviations from the Beer-Lambert law in optical estimation of lactate. Sci Rep 2021;11:13734. [Crossref] [PubMed]
- Siddon RL. Fast calculation of the exact radiological path for a three-dimensional CT array. Med Phys 1985;12:252-5. [Crossref] [PubMed]
- Gao H. Fast parallel algorithms for the x-ray transform and its adjoint. Med Phys 2012;39:7110-20. [Crossref] [PubMed]
- Henke BL, Gullikson EM, Davis JC. X-ray interactions: photoabsorption, scattering, transmission, and reflection at E= 50-30,000 eV, Z= 1-92. At Data Nucl Data Tables 1993;54:181-342. [Crossref]
- Peng FX, Hu SB, Gao ZN, Zhou W, Sun H, Yu P. Chaotic particle swarm optimization algorithm with constraint handling and its application in combined bidding model. Comput Electr Eng 2021;95:107407. [Crossref]
- Zhao H, Chen ZG, Zhan ZH, Kwong S, Zhang J. Multiple populations co-evolutionary particle swarm optimization for multi-objective cardinality constrained portfolio optimization problem. Neurocomputing 2021;430:58-70. [Crossref]
- Abbasi M, Rafiee M, Khosravi MR, Jolfaei A, Menon VG, Koushyar JM. An efficient parallel genetic algorithm solution for vehicle routing problem in cloud implementation of the intelligent transportation systems. J Cloud Comput 2020;9:1-14. [Crossref]
- Katoch S, Chauhan SS, Kumar V. A review on genetic algorithm: past, present, and future. Multimed Tools Appl 2021;80:8091-126. [Crossref] [PubMed]
- Faramarzi A, Heidarinejad M, Stephens B, Mirjalili S. Equilibrium optimizer: A novel optimization algorithm. Knowledge-Based Systems 2020;191:105190. [Crossref]
- Gupta S, Deep K, Mirjalili S. An efficient equilibrium optimizer with mutation strategy for numerical optimization. Applied Soft Computing 2020;96:106542. [Crossref]
- Fan QS, Huang HS, Yang K, Zhang SS, Yao LG, Xiong QQ. A modified equilibrium optimizer using opposition-based learning and novel update rules. Expert Syst Appl 2021;170:114575. [Crossref]
- Herman GT. Correction for beam hardening in computed tomography. Phys Med Biol 1979;24:81-106. [Crossref] [PubMed]
- Kachelriess M, Sourbelle K, Kalender WA. Empirical cupping correction: a first-order raw data precorrection for cone-beam computed tomography. Med Phys 2006;33:1269-74. [Crossref] [PubMed]
- Zhao W, Fu GT, Sun CL, Wang YF, Wei CF, Cao DQ, Que JM, Tang X, Shi RJ, Wei L, Yu ZQ. Beam hardening correction for a cone-beam CT system and its effect on spatial resolution. Chinese Physics C 2011;35:978. [Crossref]
- Schüller S, Sawall S, Stannigel K, Hülsbusch M, Ulrici J, Hell E, Kachelrieß M. Segmentation-free empirical beam hardening correction for CT. Med Phys 2015;42:794-803. [Crossref] [PubMed]
- Jia X, Yan H, Cervino L, Folkerts M, Jiang SB. A GPU tool for efficient, accurate, and realistic simulation of cone beam CT projections. Med Phys 2012;39:7368-78. [Crossref] [PubMed]





