
High-efficiency 3D black-blood thoracic aorta imaging with patch-based low-rank tensor reconstruction
Introduction
Diseases of the thoracic aorta are some of the most common causes of cardiovascular morbidity and mortality and can result in potentially catastrophic consequences (1-3). Thoracic aortic imaging can be used to diagnose aortic diseases and may help predict cardiovascular risk (4). Aortic computed tomography angiography (CTA) with intravenous iodinated contrast material is the most widely used diagnostic modality for clinical situations (5-7). However, CTA has potential risks from radiation and intravenous contrast exposure, and it is not suitable to use for repeated checks. Furthermore, CTA only enables measurement of the lumen stenosis and cannot show lesions on the vessel wall. Aortic MR imaging can accurately visualize the entire aorta without using ionizing radiation or injecting iodinated contrast material (8,9).
Black-blood (BB) vessel wall magnetic resonance imaging (MRI) has been demonstrated to be a promising technique for the assessment of thoracic aortic diseases (10,11). Through blood signal suppression, it can increase the contrast between the blood and vessel wall (12). Therefore, it can support the detection of conditions such as arterial wall thickening, aortic dissection, and vulnerable atherosclerotic plaques (13-16). In addition, the high spatial resolution can visualize and characterize the composition of atherosclerotic plaques in vivo based on MR signal intensity and can evaluate the effect of medical treatment on changes in wall thickness more precisely (12,17).
Previous studies demonstrated that 3-dimensional (3D) imaging has some advantages because it allows for improved signal-to-noise (SNR) and higher spatial resolution compared to 2D imaging (18,19). BB thoracic aortic imaging is realized by using a magnetization-preparative module before the pulse to maximize the contrast between blood and the vessel wall (20,21). In doing so, the SNR of the image may be reduced (22). The thoracic aorta vessel wall imaging with a 3D-variable flip angle (vFA) fast-spin echo (FSE) with Sampling Perfection with Application-optimized Contrasts by using different flip angle Evolutions (SPACE) has traditionally been used for the assessment of the thoracic aortic disease in clinical practice and can achieve high spatial resolution vessel wall imaging (23,24).
The BB effect of the 3D vFA-FSE is achieved by setting the initial refocusing flip angle (RFA) as low as possible and gradually increasing the RFA over the remainder of the echo train. The vFA-FSE is named CUBE (GE), SPACE (Siemens), and VISTA (Philips) by different vendors. Thus, the blood signal can be better suppressed without using any magnetization-preparative module (14,25,26), and the SNR of the vessel wall can be maintained. However, the image data can only be acquired during the middle diastole to restrain the cardiac motion artifacts, and it requires a long scan time when the 2-fold generalized autocalibrating partially parallel acquisitions (GRAPPA) reconstruction is used. The low acquisition efficiency may lead to the patient moving and is poorly tolerated by most patients.
Compressed sensing (CS) has been widely used because it can accelerate image acquisition. Recently, CS has been successfully applied to the BB imaging of carotid plaque, where it exhibited a comparable image quality to the fully sampled methods with significantly reduced scanner times (27-29). However, the image quality contains blurring, and the image contrast appears reduced for high accelerations when the conventional CS is used, such as the ℓ1-SPIRiT regularization (30).
Recently, the patch-based low-rankness of the image matrix has achieved good results in accelerating MRI by using the anatomical correlation of images locally, outperforming conventional CS reconstructions by restoring better image edges and details, and exhibiting improved overall image quality (31,32). The use of tensor structures that implicitly enforce low-rankness for accelerated imaging has been proposed (33-36). These techniques exploit the strong anatomical correlations observed in multidimensional images on a global scale, which use the entire image series as a tensor directly, or on a local scale, which extract the image patches that have higher correlations in the neighborhood and rearrange them to form local tensors. The reconstruction with patch-based low-rank tensors (Pt-LRT) using the local processing approach has been shown to outperform low-rank tensor reconstruction globally (31,36). As an extension of the matrix, the high-order tensors could better describe the data by describing multilinear latent structures beyond the pairwise interactions captured by matrices, which may enable high-resolution thoracic aorta imaging with higher accelerations while maintaining clinical image quality and scan time. Therefore, this study primarily focused on the optimization of the vFA-FSE sequence to a higher acceleration and on improving image quality with the Pt-LRT algorithm to achieve an isotropic high-resolution thoracic aorta wall imaging with clinically acceptable scan duration.
An in vivo experiment was used in this work, with the traditional GRAPPA acquisition and CS-based ℓ1-SPIRiT reconstruction being compared to determine the superiority of the proposed framework. The feasibility of the proposed method was demonstrated in 12 healthy participants and 2 patients within a 4.5 s free-breathing acquisition. Quantitative analyses of the vessel wall thickness (VWT), internal diameter (ID), lumen area (LA), and contrast-to-noise ratio (CNR) between the lumen and wall were performed on all healthy participants. Statistical analyses of the VWT, ID, and LA were used to test the measurement agreement between the Pt-LRT reconstruction and its corresponding GRAPPA sampling. Statistical analysis of the CNR between the lumen and wall was also used to test the image quality between Pt-LRT reconstruction and ℓ1-SPIRiT reconstruction.
Methods
Sequence optimization and data acquisition
The schematic and timing diagrams of the 3D T1-weighted BB modulated vFA-FSE sequence are shown in Figure 1. The Cartesian undersampling is the prospective. To minimize the cardiac motion artifacts and pulsatility artifacts, 2 image datasets of the thoracic aorta are acquired using electrocardiogram (ECG) gating triggered to the middle diastole. One data set is sampled with a variable density sampling pattern accompanied by an elliptical k-space coverage, and the other is sampled with 1D GRAPPA. A fat saturation pulse is used for magnetization preparation and is followed by the vFA-FSE acquisition.
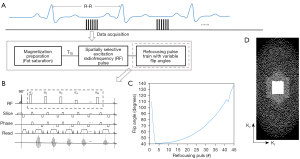
An asymmetric pulse is used for the spatially selective radiofrequency (RF) excitation, which can shorten the echo time and maximize the contrast between the aortic wall, blood, and perivascular fat. Furthermore, the echo spacing (ESP) can be shorted by employing the short nonselective RF pulses in the refocusing pulse train. A short ESP can minimize the duration of the echo train thus the reduced blurring.
The flip angle train used in the 3D vFA-FSE is shown in Figure 1C. vFA-FSE can reduce the blurring because the modulation of the refocusing flip angles keeps the magnetization relatively constant over the long echo train (37). An echo train of about 45 was used in this work to reduce the scan time.
The Cartesian trajectory with variable density is performed in the ky-kz plane, where kz is the slice direction. A fully sampled k-space center area with 32 autocalibration scan (ACS) lines for calibration in GRAPPA reconstruction. Variable density Cartesian sampling (Figure 1D) with CS is used to accelerate image acquisition, and an iterative Pt-LRT algorithm for the imaging reconstruction of sparsely undersampled k-space data (38). For each mask, a k-space center area 32×22 in size is fully sampled for the calibration in the ℓ1-SPIRiT and low-rank tensor reconstruction (Figure 1D).
Forward reconstruction model
Let be the image to be reconstructed, where , and are the number of voxels in the frequency encoding, phase encoding, and slice directions. is the acquired k-space data, where Nc denotes the number of the phase-array coils. Then, the forward reconstruction model can be given by the following formula:
where ε represents the measurement noise and E is the encoding operator (39), including the undersampled Fourier operator and the coil sensitivities, which can be formulated as E = AFS, where S denotes the coil sensitivity map, F denotes the Fourier transform operator, and A denotes the undersampling mask. The forward reconstruction model presented in Eq. [1] is usually ill-conditioned due to sub-Nyquist sampling. Therefore, regularizers that induce prior information can be incorporated into the objective function, and the image reconstruction is then formulated as an optimization problem:
where the first term represents data consistency with acquired measurements, R(·) is a regularization term, ||·||F is the Frobenius norm, and λ is the regularization parameter.
Pt-LRT reconstruction
In this study, a Pt-LRT reconstruction model with regularization is proposed to explore the global low-rankness and nonlocal self-similarity of the thoracic aorta images. The method first extracts similar 3D patches to form fourth-order tensors, and then a class of low-rank penalties is employed to explore the low-rankness of the tensors. A block matching algorithm is used to extract similar anatomical patches from X at each spatial location, after which X can be regarded as a high-order low-rank representation on a patch scale, possibly with respect to an appropriately chosen patch selection operator. Let Pp(·) denote the patch selection operator, which extracts a group of similar patches centered at pixel p from the image (
where ||·||* is the nuclear norm, ||·||1 is the L1 norm, is defined as , and λ1 is a regularization parameter. Eq. [3] can be converted into the following equivalent constrained optimization problem through variable splitting:
By using the Lagrangian optimization scheme, Eq. [4] can be rewritten as the following:
Eq. [5] can be solved through the alternating direction method of multipliers (ADMM) (41) by transforming the optimization problem into 5 subproblems:
Update on X:
Subproblem Eq. [6] could be solved through the conjugate gradient (CG) algorithm.
Update on Γp:
Subproblem Eq. [7] can be solved in 3 steps. First, high-order singular value decomposition (HOSVD) is applied to the tensors Γp, which effectively acts as a high-order denoising process. A demonstration of the HOSVD is shown in Algorithm 1 in Appendix 1. Second, the denoised tensors are rearranged to form denoised patches. Finally, the image patches are overlapping and can be combined by simple averaging (see Figure 2, Aggregation) to generate the final image estimation .

Update on Z:
Subproblem Eq. [8] can be solved with soft thresholding with the solution to , where ST(·) denotes the soft thresholding operator, which is defined as follows:
where m is an element of the image matrix, and v is the threshold.
Update on α1:
Update on α2:
Experiments
All in vivo imaging examinations were performed on 3T whole-body MRI scanners (u790, United Imaging, Shanghai, China) during free breathing. A 12-channel phased array abdomen coil and an integrated spine matrix coil (total of 24 channels) were used for signal reception. The study recruited 12 healthy volunteers (aged 20–55 years; 2 females) and 2 patients (aged 64 and 60 years; 1 male and 1 female). MR images of the whole thoracic aorta using an oblique sagittal orientation were acquired during free breathing. For each scan, both conventional GRAPPA and the proposed 3D T1-weighted vFA-FSE were acquired in the same participant. Both of the 2 imaging schemas were ECG-triggered to the mid-diastolic rest period (the trigger delay was about 500–700, depending on the cardiac cycle) to minimize flow artifacts.
The conventional GRAPPA acquisition was performed as a reference. The imaging parameters for the traditional GRAPPA were as follows: GRAPPA undersampling in the phase encoding direction with elliptical k-space scanning (the total accelerated factor was 3.06); ACS =32, 4 averages; echo time (TE)/repetition time (TR) =20.67/R-R ms; echo train length (ETL) =40–45; matrix =240×208×76; 1.2 isotropic resolution; BW =700 Hz/pixel; and spectral presaturation with inversion recovery. The average scan time was 7.5±1.8 min. Variable density Cartesian sampling had similar acquisition parameters as those for GRAPPA acquisition except for the use of a CS k-space undersampling pattern with an acceleration of 5/5.5, an average of 3.5, and a scan time that could be reduced to 4.5 min (about a 40% reduction). Then, they were reconstructed with the ℓ1-SPIRiT and the proposed Pt-LRT reconstruction.
All of the reconstructions were performed in MATLAB R2014b (MathWorks, Natick, MA, USA) and a workstation with 2 10-core 2.60-GHz Intel Xeon processors (Intel Xeon E5-2660V3 and 128 GB memory). The regularization parameter λ was determined empirically (the optimal value of λ was 0.01) by balancing the noise/artifacts and blurring in the ℓ1-SPIRiT reconstructions. For the Pt-LRT reconstruction method, all regularization parameters were also selected empirically. The size of the patch was set as 6×6×6. Before application of the ADMM, the k-space data were normalized by scaling the data to have a maximum magnitude of 1. λ1 with the value of 0.002, 0.002, 0.002, or 0.004 in the HOSVD denoising process worked well. In this study, since the size of the patch used for constructing the high-order tensor Γp is 6×6×6, if denotes the number of similar patches, the size of the resultant tensor Γp is . The number of rows for the unfolding matrix of Γp along the mode-4 (denoted by T(4)) is much larger than that of other 3 unfolding matrices of Γp along the mode-1, 2, 3 [denoted by T(1), T(2), T(3)]. We used a value of 0.004 to provide more weight for the low rankness of T(4). For the ADMM penalty parameters µ1 and µ2, and the soft thresholding threshold v , we investigated a range of values and found empirically that µ1=0.01, µ2=0.05, and v=0.01 were good initializations. Furthermore, we used varying penalty parameters to make the algorithm reach a fast convergence by increasing µ1 and µ2 with an increment in each subsequent iteration:
where iADMM denotes the ADMM iteration number, iADMM is set as 10, and the CG iteration number is set as 15. In view of the convergence numerically, the relative change in the solution between 2 consecutive iterations can be calculated and defined as follows:
where Xiter denotes the reconstructed image at the iter-th ADMM iteration. Based on our experience, the performance of Pt-LRT is sensitive to the iteration number of ADMM. The relative change stabilizes rapidly within a few iteration numbers and has no significant changes when the iteration number reaches 10. When the relative change in the solution between the 2 consecutive iterations is less than the predefined value of 4×10−3 or when the algorithm reaches the maximum iteration, the stopping criterion is defined.
The study was conducted in consistent with the Declaration of Helsinki (as revised in 2013). It was approved by the Ethics Committee at the Shenzhen Institute of Advanced Technology, Chinese Academy of Sciences (No. SIAT-IRB-180315-H0228), and written informed consent was obtained before experiments from all participants.
Image analysis
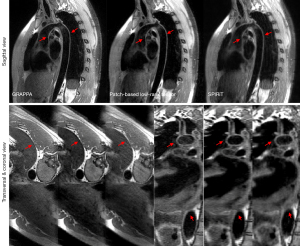
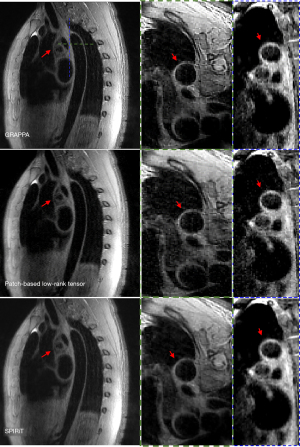
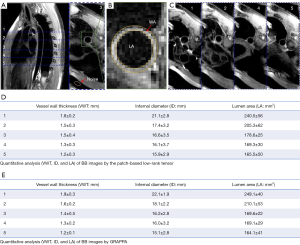
Three different spatial orientations (the transverse, coronal, and sagittal views) reconstructed by the GRAPPA, Pt-LRT, and ℓ1-SPIRiT are shown in Figures 3,4. A conventional GRAPPA sequence was used to serve as a reference for morphological (i.e., the lumen and vessel wall) quantification and image quality (i.e., CNR, SNR, and sharpness) assessment of the thoracic aorta. For each healthy participant, the thoracic aorta was divided into 5 segments from the ascending aorta to the descending aorta (Figure 5A). The lumen and outer wall contours of the vessel wall (Figure 5B) on all of the cross-sectional slices (Figure 5C) were drawn on the 2 above-described reconstructed images (GRAPPA, Pt-LRT), which were manually signed by a radiologist. Based on these contours, the VWT, ID, and LA of the 5 different levels were measured. Quantitative analysis (VWT, ID, and LA) was only used on the Pt-LRT reconstruction and its corresponding GRAPPA reference to test whether the proposed method could obtain the accurate measurement of the lumen and vessel wall with reduced imaging time. A paired t test was used to compare the quantitative analyses of the GRAPPA acquisition and the proposed method. A P value of less than 0.05 was considered statistically significant.
In addition, to evaluate the effect on image quality, the average of the wall-lumen CNR and SNR of the 5 different levels of the aorta shown in Figure 5A was measured in the 40th slice of the cross-sectional 3D vessel wall images acquired with GRAPPA, the proposed method, and ℓ1-SPIRiT reconstruction.
The CNR between the lumen blood and vessel wall was calculated using the following formula:
The SNR of the wall [SNR (wall)] and lumen [SNR(lumen)] were measured, and they were calculated using a method adopted from a previous publication (42):
where SMIWA and SMILA are the mean signal intensity of the vessel WA and the LA (Figure 5B), respectively. The mean CNR (mCNR) values for each healthy participant were acquired by averaging the measurement results of the 5 different levels of the aorta from the ascending aorta to descending aorta. NoiseSD is the standard deviation of the air signal. Furthermore, the differences in CNR between the proposed method and ℓ1-SPIRiT reconstruction were assessed using a paired t test, and the statistical significance was set to P<0.05.
The sharpness measurements of the proposed Pt-LRT, GRAPPA, and ℓ1-SPIRiT reconstruction are shown in Table 1. The sharpness quantization strategy was similar to that used in previous publications (43,44). A straight line was drawn perpendicular to the vessel wall to obtain a line profile. The sharpness of the boundary was defined based on the profile using the following equation:
Table 1
| Quantitative analysis index | GRAPPA | Patch-based low-rank tensor | ℓ1-SPIRiT |
|---|---|---|---|
| SNR (lumen) | 19.8±3.4 | 17.9±4.2 | 20.2±1.3 |
| SNR (wall) | 71.2±6.5 | 67.3±7.6 | 59.1±8.1 |
| CNR | 51.4±3.1 | 49.4±3.4 | 38.9±6.8 |
| Sharpness | 0.83±0.02 | 0.78±0.05 | 0.69±0.12 |
Data are presented as the mean ± SD. CNR, contrast-to-noise ratio; SNR, signal-to-noise ratio; GRAPPA, generalized autocalibrating partially parallel acquisitions; SNR (lumen), the SNR of the lumen area; SNR (wall), the SNR of the wall area.
where d is defined as the distance between positions where the intensity values of the profile can be changed from 0.2 to 0.8 of the difference between the maximum and minimum intensity values (in millimeters). The sharpness of the vessel wall from the inner and outer boundaries was measured from ascending aorta to descending thoracic aorta and averaged. The mean sharpness (Msharpness) values of each healthy participant were acquired by averaging the measurement results of the 5 different levels of the aorta from the ascending aorta to descending aorta. We compared these quantitative image analyses of the 3 methods.
Furthermore, since the constructed patch-based tensors are fourth-order tensors, we cannot visualize them. To show the low rankness of the patches, we selected a tensor at the ascending aorta region from the constructed patch-based tensors and visualized its 4 unfoldings [T(1), T(2), T(3), T(4)]. The corresponding singular values demonstrated the low rankness of the unfoldings.
Results
Representative results of the thoracic MR images with 3 different views are shown in Figures 3,4. A good depiction of the aortic arch and clear outer and inner aortic wall delineation in the descending aorta was obtained by the proposed reconstruction. The image showed a vessel definition and sharpness comparable to that of GRAPPA (the reference). Boundary blurring/unclear delineation existed between the wall and surroundings, as well as the outer wall, when ℓ1-SPIRiT reconstruction was performed, as shown by the red arrowheads shown in Figures 3,4 on the coronal and transverse views. Therefore, the proposed approach could provide better quality images of the thoracic aorta compared with the ℓ1-SPIRiT approach. However, due to slow blood flow in the thoracic aorta (the white arrowheads), poor blood-signal suppression was present in the aortic arch because of the incomplete flow void.
The results of the quantitative analysis of VWT, ID, and LA of the BB images obtained by the proposed method are shown in Figures 5,6. The means and standard deviations were measured for all healthy volunteers for the 5 different levels. As a whole, the lumen gradually became smaller from the ascending aorta to the descending aorta. There were no significant differences between the GRAPPA imaging and the proposed method in VWT, ID, or LA (P<0.05). Linear regression was often used to test the measurement agreement in morphological and functional parameters between Pt-LRT and corresponding GRAPPA reference. Bland-Altman analysis was also used to determine the extent of agreement. Based on the Bland-Altman plots (Figure 6B,6D,6F), excellent agreements of VWT, ID, and LA measurement results were observed between the Pt-LRT and GRAPPA image sets. For VWT measurements, an absolute mean difference of −0.003 with a 95% limits of agreement from −0.014 to 0.0086 was obtained; for ID measurements, −0.037 with a 95% limits of agreement from −1.05 to 0.98 was obtained; and for LA measurements, −3.20 with a 95% limits of agreement from −24.85 to 18.45 was obtained. Therefore, according to the linear regression and Bland-Altman analysis, there were no significant differences and the agreement was excellent between the GRAPPA imaging and the proposed method in VWT, ID, and LA.
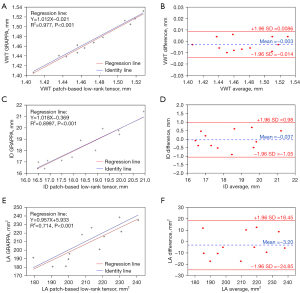
The mean CNR measurements for the aorta were 49.4±3.4 and 38.9±6.8 for the proposed reconstruction and ℓ1-SPIRiT, respectively. CNR between the arterial wall and the lumen was 21% less with ℓ1-SPIRiT compared with the proposed reconstruction. The results demonstrated an improved image contrast ratio compared to the ℓ1-SPIRiT reconstruction. A paired t test (P<0.05) was performed to identify statistically significant differences in CNR. The analysis of the ℓ1-SPIRiT reconstruction had a significant difference compared to that of the proposed reconstruction according to the SNR measurements of the proposed Pt-LRT, GRAPPA, and ℓ1-SPIRiT reconstruction, as shown in Table 1. SNR (lumen) in all regions of interest (ROIs) of the thoracic aorta were significantly lower with Pt-LRT than with GRAPPA or ℓ1-SPIRiT. The CNR and SNR (wall) were significantly higher with Pt-LRT than with ℓ1-SPIRiT. Moreover, Pt-LRT had a slightly lower SNR (wall) and CNR than did GRAPPA, but this difference was not significant. However, there were no significant differences between GRAPPA and Pt-LRT in SNR and CNR. Furthermore, in sharpness quantification, there were no significant differences between the Pt-LRT and GRAPPA in the thoracic aorta wall imaging, whereas the sharpness was significantly higher with Pt-LRT than with ℓ1-SPIRiT reconstruction. Therefore, the tensor low-rank model does not affect the CNR evaluation, although the tensor low-rank reconstruction results appear a little smoother.
Figure 7A presents the 4 unfoldings of the tensor along different modes, and Figure 7B plots the corresponding singular values of the unfoldings to demonstrate the low-rankness of the patch-based tensor. We have added a detailed description of the HOSVD algorithm in Appendix 1.
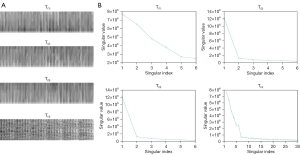
Figure 8 shows the BB imaging of the aortic arch in a 64-year-old male patient with an aortic aneurysm in the left side of the aortic arch that was acquired using the 3D vFA-FSE sequence. An aneurysm was clearly depicted in all 3 views (red arrowheads). The motion artifacts (yellow arrowhead) could be seen in the GRAPPA imaging because of the long imaging time.
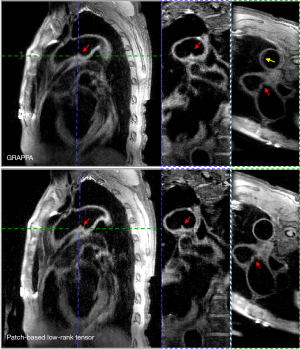
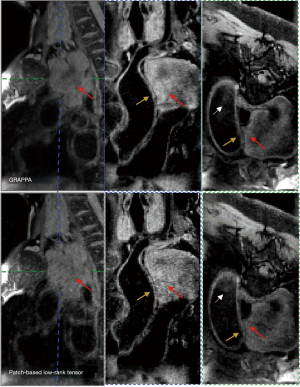
Figure 9 shows the imaging results of a female patient (60 years old) with a large saccate superior vena cava tumor near the arch of the aorta (red arrowheads). Vortex flow patterns were present in the ascending aorta. Although, poor blood-signal suppression was seen in the transverse multiplanar reformation (MPR) images due to the vortex flow in the ascending aorta (white arrowheads). The vessel walls were clearly depicted, and the definition of the tumor boundary could also be clearly visualized on the transverse and coronal views of the BB image.
Discussion
Three-dimensional vFA-FSE is commonly used to noninvasively assess the vulnerable plaques in the thoracic aorta. Recently, several blood-imaging methods with multicontrast have been proposed to obtain the bright MR angiography and BB vessel wall images simultaneously. Examples of related studies include Yoneyama et al. (45), who reported a method called REACT (Relaxation-Enhanced Angiography without Contrast and Triggering (REACT) with Multiple Delays (REACT-MD), and a method reported by Hu et al. (46) called the MT-MACS(Multitasking-based Multidimensional Assessment Of Cardiovascular System). In addition, Tachikawa et al. (11) proposed a novel method named Bright and Dark Blood Images with Multishot Gradient-Echo EPI (BRIDGE) to evaluate MRA and VWI in the thoracic aorta. However, the spatial resolution is lower with these methods. In order to image the thoracic aorta, especially for the aortic vessel wall, a higher spatial resolution with isotropic resolution is critical for the more detailed depiction of the vessel wall, and partial volume effects can be reduced. However, higher spatial resolution may lead to an increased scan time.
For the low-rank tensor reconstruction, a global low-rank tensor model that captured data correlation in multiple dimensions, including spatiotemporal or spatiospectral correlation, was applied to reconstruction images from undersampled data in the study by He et al. (33). In the study by Guo et al. (36), the functional MRI (fMRI) time series was broken into nonoverlapping time blocks and used to construct the patch-tensors, which only imposed low-rankness on temporal blocks instead of the whole fMRI time series. In our study, overlapping patches of the whole image were used to construct the Pt-LRTs, which exploited the similarities among neighboring pixels and nonlocal pixels over the whole image and may be more rank-deficient.
In this paper, we present a fast imaging strategy for 3D BB thoracic aorta imaging and demonstrate its feasibility in healthy participants and patients with thoracic aortic diseases. The results show that the optimized vFA-FSE sequence combined with the patch-based low-rank reconstruction can achieve 3D thoracic aorta VWI under free-breathing conditions within ~4.5 min. The visualization and sharpness of the vessel wall and the definition of the tissue boundary are comparable to those of the traditional GRAPPA approach, which takes approximately more than 7.5 min. On average, the proposed method reduces the acquisition time by 1.7 min compared with the traditional GRAPPA approach. The reconstructed results also show superior CNR, vessel sharpness, and delineation of the outer vessel wall with the proposed patch-based low-rank reconstruction compared to the ℓ1-SPIRiT reconstruction. The image quality contained blurring and reduced image contrast for high accelerations when the ℓ1-SPIRiT was used. The higher image quality and clear boundary definition of the vessel wall enabled by our method supported a higher spatial resolution. Thus, a more accurate measurement of the small changes in vessel wall dimensions could benefit from higher resolution. In this work, the spatial resolution was 1.2×1.2×1.2 mm3 with isotropic resolution. The higher resolution is highly desirable to better delineate the vessel wall of the aortic and reduce the partial volume effect.
In this study, we used an average of 4 to increase the SNR of the acquired image data. However, in order to reduce the free-induction-decay artifacts, we averaged the image data along the repetition dimension. Therefore, the data used for reconstruction were a single-frame data set, and the tensor might not have been low rank if we constructed the whole 3D data set as a global tensor. Therefore, we did not include the global low-rank tensor as a reference for the reconstruction comparison.
Furthermore, respiratory motion is another motion type that would affect the image quality of cardiac MR images. Generally, the diaphragmatic navigator-gated technique (47) or respiratory-ordered phase encoding (48) is used to reduce respiratory motion artifacts. In our work, these respiratory corrections were not used with the vFA-FSE sequence, and these strategies may improve image quality. In order to trade off the imaging time and respiratory artifacts, multiple signals (with scans repeated 3 or 4 times) were averaged to minimize respiratory and other motion-related artifacts, as has been done previously (49,50).
First, all the imaging data were obtained in the mid-diastolic period to realize BB imaging. However, this strategy may result in severe motion artifacts in patients with cardiac arrhythmias and irregular breathing rhythms. Furthermore, the magnetic inhomogeneity in the thorax leads to SNR reduction of the ascending aorta and partial signal loss (51). The image quality can be improved by shimming the ascending aorta in focus; however, this method may not be suitable for patients with respiratory disorders or arrhythmia. Second, with the proposed method, conditions of cardiac hypofunction, vortex flow patterns, or reduced blood flow can decrease the BB effect (i.e., aortic arch) due to insufficient blood flow (24). As shown in Figure 3, the slow blood flow in the thoracic aorta or the vortex flow in the ascending aorta (Figure 7) can lead to an incomplete flow void, thus causing poor blood-signal suppression in the aortic arch. Third, with the proposed method, the acquisition time is related to the R-R interval, with a shorter R-R interval requiring a reduced acquisition time. In other words, with a lower heart rate and a longer R-R interval, the acquisition time increases. Therefore, the imaging time across different individuals may vary according to the difference in heart rates. The ETL can be increased to shorten the acquisition time in individuals with a slow heart rate. Regardless, most can be completed within 4.5 min.
Our study had some limitations. First, the reconstruction time is a major issue that needs to be shortened. In this work, to accelerate the process, patch extraction was implemented in C++ using graphical processing units, and parallel computing was applied in the HOSVD denoising of tensors for each group of similar patches. The reconstruction time was about 1 hour. The reconstruction time may be further shortened by implementing the whole reconstruction in C++, which will be implemented in future studies. Furthermore, algorithm optimization and use of graphics processing units or parallel processing methods should help speed up the reconstruction. Second, a larger number of clinical cases are needed to validate the feasibility of the proposed technique. In addition, various thoracic aortic diseases, including aortic dissection, aortic aneurysm, aortic atherosclerosis, and vasculitis, need to be further assessed by our developed method. Thus, a large number of patients with different types of thoracic aortic diseases need to be recruited to test the utility of this method.
Nonetheless, the good image quality of the thoracic aorta images is sufficient for the proposed 3D MR imaging technique to diagnose diseases of the thoracic aorta.
Conclusions
This work proposed a high-resolution, 3D MRI technique for thoracic aorta imaging by optimizing a vFA-FSE technique with iterative Pt-LRT reconstruction. The results demonstrate that the proposed scheme is approximately 1.7 times faster than the GRAPPA acquisition and can yield comparable image quality. The reconstruction results are also better than those of the ℓ1-SPIRiT reconstruction in terms of the thoracic aorta vessel delineation, vessel wall sharpness, and improved aortic wall-lumen CNR. Further evaluation of the proposed method in patients with various thoracic aortic diseases will be conducted to determine its clinical use in the future.
Acknowledgments
Funding: This work was partially supported by grants from the National Key R&D Program of China (No. 2021YFF0501402), the National Natural Science Foundation of China (Nos. 81901736, 12226008, 61871373, 81830056, 62201561, 81971611, 62271474, 61771463, U1805261, and 12026603), the Strategic Priority Research Program of the Chinese Academy of Sciences (No. XDB25000000 and XDC07040000), the China Postdoctoral Science Foundation (No. 2022M723302), the Guangdong Basic and Applied Basic Research Foundation (Nos. 2021A1515110540 and 2020B1212060051), the Engineering Laboratory Program of the Chinese Academy of Sciences (No. KFJ-PTXM-012), the High-level Talent Program in the Pearl River Talent Plan of Guangdong Province (No. 2019QN01Y986), the Shenzhen Science and Technology Program (No. RCYX20210609104444089 and JCYJ20210324115810030), the Shenzhen Peacock Plan Team Program (No. KQTD20180413181834876 and KCXF20211020163408012), the Science and Technology Plan Program of Guangzhou (No. 202007030002), the Key Field R&D Program of Guangdong Province (No. 2018B030335001), and the Key Technology and Equipment R&D Program of Major Science and Technology Infrastructure of Shenzhen (Nos. 202100102 and 202100104).
Footnote
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at https://qims.amegroups.com/article/view/10.21037/qims-22-702/coif). DL serves as an unpaid editorial board member of Quantitative Imaging in Medicine and Surgery. The other authors have no conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013). The study was approved by the Ethics Committee at the Shenzhen Institute of Advanced Technology, Chinese Academy of Sciences (No. SIAT-IRB-180315-H0228), and written informed consent was obtained from all patients.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- François CJ, Carr JC. MRI of the thoracic aorta. Magn Reson Imaging Clin N Am 2007;15:639-51. vii. [Crossref] [PubMed]
- Stanger OH, Pepper JR, Svensson LG. Surgical Management of Aortic Pathology: Current Fundamentals for the Clinical Management of Aortic Disease. Vienna: Springer; 2019.
- Sun Z. Quantitative cardiovascular imaging. Quant Imaging Med Surg 2014;4:297-9. [PubMed]
- Jaffer FA, O'Donnell CJ, Larson MG, Chan SK, Kissinger KV, Kupka MJ, Salton C, Botnar RM, Levy D, Manning WJ. Age and sex distribution of subclinical aortic atherosclerosis: a magnetic resonance imaging examination of the Framingham Heart Study. Arterioscler Thromb Vasc Biol 2002;22:849-54. [Crossref] [PubMed]
- Raptopoulos V, Rosen MP, Kent KC, Kuestner LM, Sheiman RG, Pearlman JD. Sequential helical CT angiography of aortoiliac disease. AJR Am J Roentgenol 1996;166:1347-54. [Crossref] [PubMed]
- Frazao C, Tavoosi A, Wintersperger BJ, Nguyen ET, Wald RM, Ouzounian M, Hanneman K. Multimodality Assessment of Thoracic Aortic Dimensions: Comparison of Computed Tomography Angiography, Magnetic Resonance Imaging, and Echocardiography Measurements. J Thorac Imaging 2020;35:399-406. [Crossref] [PubMed]
- Sun Z, Al Moudi M, Cao Y. CT angiography in the diagnosis of cardiovascular disease: a transformation in cardiovascular CT practice. Quant Imaging Med Surg 2014;4:376-96. [PubMed]
- Kim TJ, Lee KH, Choe YH, Lee KS. Acute Aortic Diseases: Evaluation with Computed Tomography and Magnetic Resonance Imaging. In: Emergency Chest Radiology. Singapore: Springer, 2021: 63-88.
- Hoyer UCI, Lennartz S, Abdullayev N, Fichter F, Jünger ST, Goertz L, Laukamp KR, Gertz RJ, Grunz JP, Hohmann C, Maintz D, Persigehl T, Kabbasch C, Borggrefe J, Weiss K, Pennig L. Imaging of the extracranial internal carotid artery in acute ischemic stroke: assessment of stenosis, plaques, and image quality using relaxation-enhanced angiography without contrast and triggering (REACT). Quant Imaging Med Surg 2022;12:3640-54. [Crossref] [PubMed]
- Zhang Z, Fan Z, Carroll TJ, Chung Y, Weale P, Jerecic R, Li D. Three-dimensional T2-weighted MRI of the human femoral arterial vessel wall at 3.0 Tesla. Invest Radiol 2009;44:619-26. [Crossref] [PubMed]
- Tachikawa Y, Hamano H, Yoshikai H, Ikeda K, Maki Y, Hirata K, Takahashi Y, Matake K. Three-dimensional multicontrast blood imaging with a single acquisition: Simultaneous non-contrast-enhanced MRA and vessel wall imaging in the thoracic aorta. Magn Reson Med 2022;88:617-32. [Crossref] [PubMed]
- Fayad ZA, Nahar T, Fallon JT, Goldman M, Aguinaldo JG, Badimon JJ, Shinnar M, Chesebro JH, Fuster V. In vivo magnetic resonance evaluation of atherosclerotic plaques in the human thoracic aorta: a comparison with transesophageal echocardiography. Circulation 2000;101:2503-9. [Crossref] [PubMed]
- Henningsson M, Zahr RA, Dyer A, Greil GF, Burkhardt B, Tandon A, Hussain T. Feasibility of 3D black-blood variable refocusing angle fast spin echo cardiovascular magnetic resonance for visualization of the whole heart and great vessels in congenital heart disease. J Cardiovasc Magn Reson 2018;20:76. [Crossref] [PubMed]
- Eikendal AL, Blomberg BA, Haaring C, Saam T, van der Geest RJ, Visser F, Bots ML, den Ruijter HM, Hoefer IE, Leiner T. 3D black blood VISTA vessel wall cardiovascular magnetic resonance of the thoracic aorta wall in young, healthy adults: reproducibility and implications for efficacy trial sample sizes: a cross-sectional study. J Cardiovasc Magn Reson 2016;18:20. [Crossref] [PubMed]
- Li L, Chai JT, Biasiolli L, Robson MD, Choudhury RP, Handa AI, Near J, Jezzard P. Black-blood multicontrast imaging of carotid arteries with DANTE-prepared 2D and 3D MR imaging. Radiology 2014;273:560-9. [Crossref] [PubMed]
- Meng Y, Mo Z, Hao J, Peng Y, Yan H, Mu J, Ma D, Zhang X, Li Y. High-resolution intravascular magnetic resonance imaging of the coronary artery wall at 3.0 Tesla: toward evaluation of atherosclerotic plaque vulnerability. Quant Imaging Med Surg 2021;11:4522-9. [Crossref] [PubMed]
- Toussaint JF, LaMuraglia GM, Southern JF, Fuster V, Kantor HL. Magnetic resonance images lipid, fibrous, calcified, hemorrhagic, and thrombotic components of human atherosclerosis in vivo. Circulation 1996;94:932-8. [Crossref] [PubMed]
- Botnar RM, Kim WY, Börnert P, Stuber M, Spuentrup E, Manning WJ. 3D coronary vessel wall imaging utilizing a local inversion technique with spiral image acquisition. Magn Reson Med 2001;46:848-54. [Crossref] [PubMed]
- Kim WY, Stuber M, Börnert P, Kissinger KV, Manning WJ, Botnar RM. Three-dimensional black-blood cardiac magnetic resonance coronary vessel wall imaging detects positive arterial remodeling in patients with nonsignificant coronary artery disease. Circulation 2002;106:296-9. [Crossref] [PubMed]
- Koktzoglou I, Li D. Diffusion-prepared segmented steady-state free precession: Application to 3D black-blood cardiovascular magnetic resonance of the thoracic aorta and carotid artery walls. J Cardiovasc Magn Reson 2007;9:33-42. [Crossref] [PubMed]
- Koktzoglou I, Kirpalani A, Carroll TJ, Li D, Carr JC. Dark-blood MRI of the thoracic aorta with 3D diffusion-prepared steady-state free precession: initial clinical evaluation. AJR Am J Roentgenol 2007;189:966-72. [Crossref] [PubMed]
- Qiao Y, Steinman DA, Qin Q, Etesami M, Schär M, Astor BC, Wasserman BA. Intracranial arterial wall imaging using three-dimensional high isotropic resolution black blood MRI at 3.0 Tesla. J Magn Reson Imaging 2011;34:22-30. [Crossref] [PubMed]
- Mihai G, Varghese J, Lu B, Zhu H, Simonetti OP, Rajagopalan S. Reproducibility of thoracic and abdominal aortic wall measurements with three-dimensional, variable flip angle (SPACE) MRI. J Magn Reson Imaging 2015;41:202-12. [Crossref] [PubMed]
- Nakagawa K, Kinosada M, Tabuchi T. The optimal scanning method for three-dimen-sional T1-weighted black-blood turbo spin-echo MRI in the aortic arch. Arts Sci 2019:39–43.
- Yoneyama M, Nakamura M, Tabuchi T, Takemura A, Obara M. Optimization of 3D-variable refocusing flip angle RARE imaging for high-resolution volumetric black-blood angiography. Radiol Phys Technol 2012;5:270-6. [Crossref] [PubMed]
- Cho SJ, Jung SC, Suh CH, Lee JB, Kim D. High-resolution magnetic resonance imaging of intracranial vessel walls: Comparison of 3D T1-weighted turbo spin echo with or without DANTE or iMSDE. PLoS One 2019;14:e0220603. [Crossref] [PubMed]
- Makhijani MK, Balu N, Yamada K, Yuan C, Nayak KS. Accelerated 3D MERGE carotid imaging using compressed sensing with a hidden Markov tree model. J Magn Reson Imaging 2012;36:1194-202. [Crossref] [PubMed]
- Yuan J, Usman A, Reid SA, King KF, Patterson AJ, Gillard JH, Graves MJ. Three-dimensional black-blood T(2) mapping with compressed sensing and data-driven parallel imaging in the carotid artery. Magn Reson Imaging 2017;37:62-9. [Crossref] [PubMed]
- Zhu C, Tian B, Chen L, Eisenmenger L, Raithel E, Forman C, Ahn S, Laub G, Liu Q, Lu J, Liu J, Hess C, Saloner D. Accelerated whole brain intracranial vessel wall imaging using black blood fast spin echo with compressed sensing (CS-SPACE). MAGMA 2018;31:457-67. [Crossref] [PubMed]
- Zhang C, Moeller S, Demirel OB, Uğurbil K, Akçakaya M. Residual RAKI: A hybrid linear and non-linear approach for scan-specific k-space deep learning. Neuroimage 2022;256:119248. [Crossref] [PubMed]
- Yaman B, Weingärtner S, Kargas N, Sidiropoulos ND, Akçakaya M. Low-Rank Tensor Models for Improved Multi-Dimensional MRI: Application to Dynamic Cardiac T (1) Mapping. IEEE Trans Comput Imaging 2019;6:194-207. [Crossref] [PubMed]
- Hao R, Su Z. A patch-based low-rank tensor approximation model for multiframe image denoising. J Comput Appl Math 2018;329:125-33. [Crossref]
- He J, Liu Q, Christodoulou AG, Ma C, Lam F, Liang ZP. Accelerated High-Dimensional MR Imaging With Sparse Sampling Using Low-Rank Tensors. IEEE Trans Med Imaging 2016;35:2119-29. [Crossref] [PubMed]
- Christodoulou AG, Shaw JL, Nguyen C, Yang Q, Xie Y, Wang N, Li D. Magnetic resonance multitasking for motion-resolved quantitative cardiovascular imaging. Nat Biomed Eng 2018;2:215-26. [Crossref] [PubMed]
- Liu Y, Yi Z, Zhao Y, Chen F, Feng Y, Guo H, Leong ATL, Wu EX. Calibrationless parallel imaging reconstruction for multislice MR data using low-rank tensor completion. Magn Reson Med 2021;85:897-911. [Crossref] [PubMed]
- Guo S, Fessler JA, Noll DC. High-Resolution Oscillating Steady-State fMRI Using Patch-Tensor Low-Rank Reconstruction. IEEE Trans Med Imaging 2020;39:4357-68. [Crossref] [PubMed]
- Mugler JP 3rd. Optimized three-dimensional fast-spin-echo MRI. J Magn Reson Imaging 2014;39:745-67. [Crossref] [PubMed]
- Bustin A, Lima da Cruz G, Jaubert O, Lopez K, Botnar RM, Prieto C. High-dimensionality undersampled patch-based reconstruction (HD-PROST) for accelerated multi-contrast MRI. Magn Reson Med 2019;81:3705-19. [Crossref] [PubMed]
- Otazo R, Candès E, Sodickson DK. Low-rank plus sparse matrix decomposition for accelerated dynamic MRI with separation of background and dynamic components. Magn Reson Med 2015;73:1125-36. [Crossref] [PubMed]
- Akçakaya M, Basha TA, Goddu B, Goepfert LA, Kissinger KV, Tarokh V, Manning WJ, Nezafat R. Low-dimensional-structure self-learning and thresholding: regularization beyond compressed sensing for MRI reconstruction. Magn Reson Med 2011;66:756-67. [Crossref] [PubMed]
- Boyd S, Parikh N, Chu E, Peleato B, Eckstein J. Distributed optimization and statistical learning via the alternating direction method of multiplier. Found Trends Mach Learn 2011;3:1-122. [Crossref]
- Zhu C, Haraldsson H, Faraji F, Owens C, Gasper W, Ahn S, Liu J, Laub G, Hope MD, Saloner D. Isotropic 3D black blood MRI of abdominal aortic aneurysm wall and intraluminal thrombus. Magn Reson Imaging 2016;34:18-25. [Crossref] [PubMed]
- Larson AC, Kellman P, Arai A, Hirsch GA, McVeigh E, Li D, Simonetti OP. Preliminary investigation of respiratory self-gating for free-breathing segmented cine MRI. Magn Reson Med 2005;53:159-68. [Crossref] [PubMed]
- Zhu C, Haraldsson H, Tian B, Meisel K, Ko N, Lawton M, Grinstead J, Ahn S, Laub G, Hess C, Saloner D. High resolution imaging of the intracranial vessel wall at 3 and 7 T using 3D fast spin echo MRI. MAGMA 2016;29:559-70. [Crossref] [PubMed]
- Yoneyama M, Zhang S, Hu HH, Chong LR, Bardo D, Miller JH, Toyonari N, Katahira K, Katsumata Y, Pokorney A, Ng CK, Kouwenhoven M, Van Cauteren M. Free-breathing non-contrast-enhanced flow-independent MR angiography using magnetization-prepared 3D non-balanced dual-echo Dixon method: A feasibility study at 3 Tesla. Magn Reson Imaging 2019;63:137-46. [Crossref] [PubMed]
- Hu Z, Christodoulou AG, Wang N, Shaw JL, Song SS, Maya MM, Ishimori ML, Forbess LJ, Xiao J, Bi X, Han F, Li D, Fan Z. Magnetic resonance multitasking for multidimensional assessment of cardiovascular system: Development and feasibility study on the thoracic aorta. Magn Reson Med 2020;84:2376-88. [Crossref] [PubMed]
- Amano Y, Takahama K, Kumita S. Non-contrast-enhanced MR angiography of the thoracic aorta using cardiac and navigator-gated magnetization-prepared three-dimensional steady-state free precession. J Magn Reson Imaging 2008;27:504-9. [Crossref] [PubMed]
- Bailes DR, Gilderdale DJ, Bydder GM, Collins AG, Firmin DN. Respiratory ordered phase encoding (ROPE): a method for reducing respiratory motion artefacts in MR imaging. J Comput Assist Tomogr 1985;9:835-8. [Crossref] [PubMed]
- Stemerman DH, Krinsky GA, Lee VS, Johnson G, Yang BM, Rofsky NM. Thoracic aorta: rapid black-blood MR imaging with half-Fourier rapid acquisition with relaxation enhancement with or without electrocardiographic triggering. Radiology 1999;213:185-91. [Crossref] [PubMed]
- Wang Y, Riederer SJ, Ehman RL. Respiratory motion of the heart: kinematics and the implications for the spatial resolution in coronary imaging. Magn Reson Med 1995;33:713-9. [Crossref] [PubMed]
- Kellman P, McVeigh ER. Image reconstruction in SNR units: a general method for SNR measurement. Magn Reson Med 2005;54:1439-47. [Crossref] [PubMed]


