
Multi-robot task assignment for serving people quarantined in multiple hotels during COVID-19 pandemic
Introduction
The outbreak of the coronavirus disease 2019 (COVID-19) is a massive threat to global health, and has also posed critical challenges to other aspects of our lives such as tourism, transportation, and the industrial supply chain (1,2). To reduce the spread of the virus, minimizing inter-personal contact is a key strategy, which is widely adopted by many nations nowadays (3). Here, robots have great potential for disinfection, delivering medications and food, and reconnaissance (e.g., body temperature measurement as shown in Figure 1 and oropharyngeal swabs) (5). Some studies have investigated the deployment of multiple robots for the combat with the COVID-19 (6-8). In (6), the task assignment for patient-carrying robots to transfer patients to a COVID-19 hall and the task assignment for service-providing robots to deliver medicines and food to the patients on time are studied based on the Q-learning approach. Blockchain technology has been investigated for controlling and managing multi-drone collaboration for transporting goods and medical supplies to quarantine areas experiencing an epidemic outbreak (7,8). For most of the discussed scenarios, the deployed multiple robots need to efficiently visit a set of target locations to perform some missions such as disinfection, delivering medications, and temperature measurement for the people in quarantine areas. This is the typical multi-robot multi-target visiting task assignment problem, which has attracted increasing attention due to its wide applications in logistics, terrain mapping, and environmental monitoring (9).

The task assignment problem for a team of vehicles to visit a set of target locations while trying to minimize the robots’ total travel time (10,11) or distance (12,13) is a variant of the vehicle routing problem (VRP) (14). For the VRP, a fleet of vehicles with limited capacity must deliver goods from one or more depots to a group of customers, which is an NP-hard problem (14). This implies that an extremely long computational running time is generally required to obtain the optimal solution as the numbers of vehicles and customers grow. Consequently, many heuristic task assignment algorithms have been designed to solve the VRP (15-18). For the green VRP, a memetic algorithm was proposed in (18), where a TSP route is first computed to encode the solution. When the travel cost matrix, storing the travel cost for a robot to move between each two target locations, respects the triangular inequality as well as being symmetric, the algorithm designed in (19) guarantees that the robots’ total travel cost to visit a group of target locations is at most twice the optimal value.
Some multi-robot task assignment problems have been shown to be NP-hard (9,20), where heuristic algorithms are usually designed to calculate near-optimal solutions. In (21), a consensus-based bundle algorithm was constructed for task assignment of multiple robots that communicate over connected networks. An iterated local search algorithm with adaptive neighborhood selection was proposed for the pickup and delivery problem with time windows in (22). In (23), a genetic algorithm was constructed for unmanned aerial vehicles (UAVs) to visit multiple target locations while respecting the priority for visiting each target location and the vehicles’ capacity constraint. Monotonic algorithms were proposed in (10) to minimize the time when all the target locations are occupied by robots within a limited communication range. Later on, to minimize robots’ total travel distance until all target locations are occupied, decentralized algorithms were proposed in (12). However, in (10) and (12), the robots’ number is equal to the targets’ number, where a robot stops moving upon reaching its assigned target location. In (11), several dynamic task assignment algorithms were proposed for multiple vehicles to visit a group of target locations, where some target locations are dynamically generated during the vehicles’ movement. Integrated with Dubins car model, a genetic algorithm was designed for multi-UAV task assignment respecting the vehicles’ limited turning radius (24). However, most of the discussed task assignment algorithms have been developed assuming that the robots can continue performing the target-visiting tasks, which doesn’t consider the robots’ limited operation time.
In (25), a decentralized pandemic alerting framework has been designed to provide collaborative and intelligent solutions for digital twins based on blockchain, which has the potential ability to guarantee decentralized data storage and scalable peer-to-peer communication for smart healthcare in the fight against COVID-19. To estimate the risk level and the multifold mortality rate of COVID-19 in diabetic patients, a COVID-19 risk prediction model has been proposed in (26) for diabetic patients based on a fuzzy inference system and machine learning approaches. To deal with fake news during the COVID-19 epidemic, a hybrid deep learning model that integrates long short-term memory and a convolutional neural network has been constructed in (27). Experimental results show that the model outperforms six other machine learning models and two deep learning models. In (28), a concrete ledger-based collaborative digital twins framework that focuses on distributed consensus algorithms and real-time operational data analytics has been designed.
This paper investigates the task assignment problem for a fleet of dispersed robots to visit a set of prescribed hotels for temperature checks or oropharyngeal swabs for the people who have been quarantined in the hotels while trying to minimize the robots’ total operation time. The task assignment problem is first formulated as an optimization problem, and then several marginal cost based algorithms are designed. Our main contributions are as follows: firstly, a lower bound on the robots’ total operation time to serve all the people is constructed, which can be used to approximately evaluate the performance of the designed algorithms in relation to the optimal solutions. Second, several marginal cost-based algorithms are proposed. Simulation and experimental results show that these algorithms have better performance than the popular genetic algorithm.
Methods
Problem formulation
A fleet of m dispersed homogeneous robots needs to visit a set of n prescribed hotels for temperature assessment or oropharyngeal swabs for the people quarantined in the hotels while minimizing the robots’ total operation time. When a robot is used to check body temperature or take oropharyngeal swabs for each person, it is assumed that the same amount of average time is needed for each person. Each robot can visit multiple hotels sequentially within its limited operation time, and each hotel requires only one robot to provide the service. We assume that the robots move at a constant speed and their number and maximum operation time are sufficient to serve the people quarantined in all the hotels.
The n prescribed hotels for quarantine are indexed with 1,...,n, and let be the set of these indices. Let ci be the number of the persons quarantined in hotel i for each . It is assumed that a fixed average operation time ot is needed by a robot for body temperature assessment or oropharyngeal swabs for each person. Then, the total time that a robot needs to serve the ci people quarantined in hotel i is ciot. We use to denote the indices of the m robots, and use to contain the indices of the v robots’ initial locations. Let the constant variable v be the robots’ moving speed when moving between different hotels, and use L as the maximum operation time of each robot.
Let denote the time for a robot to travel from i to j for each pair of distinct , which is in proportion to the Euclidean distance between i and j under the constant v, i.e., . Obviously for each , . Then, given the robots’ maximum operation time L, the robots’ number m is set at least
where , and the ceiling function [a] leads to the smallest integer greater than or equal to a positive number a. To enable that each robot is viable to serve all of the people quarantined in each hotel, the maximum operation time of each robot should satisfy .
Let the decision variable equal one if and only if it is planned that robot k moves directly from location i to a distinct location j. Thus, xiik=0 for each and . The task-assignment mapping is one if and only if all the people quarantined in hotel i will be served by robot k. Let robot k’s remaining operation time be rki after serving all the people quarantined in hotel , which is initially set as . Then, the objective of minimizing the robots’ total operation time to serve all the people quarantined in the n hotels is to minimize
subject to
Constraint Eq. [3] guarantees that the people quarantined in hotel j will be served by robot k if it is planned that robot k will move to the hotel location i; Eq. [4] requires that the people quarantined in each hotel i will be served by one and only one robot; Eqs. [5] and [6] illustrate the remaining operation time of each robot after successively serving the people quarantined in two hotels i and j; Eq. [7] guarantees that the maximum operation time of each robot is satisfied; Eq. [8] implies that at most m robots can be used for the task assignment; and Eq. [9] ensures that the decision variables xijk and yik are binary variables.
Remark 1: the task assignment problem Eq. [2] is a variant of the open multiple traveling salesman problem (OMTSP) (29), which is known to be NP-hard (20).
Task assignment algorithms
It is generally costly to solve Eq. [2] optimally due to the problem’s NP-hardness. Then, it is natural to design heuristic algorithms to find sub-optimal solutions quickly. In this section, several marginal-cost-based task assignment algorithms are designed to assign the hotel-serving tasks to the multiple robots.
Total serving time based marginal cost algorithm
Inspired by the marginal-cost-based clustering strategy designed in (30), this section first introduces a total serving time based marginal cost algorithm (TSTMCA), which assigns the hotel-serving tasks to the robots based on the sum of the time incurred for each robot to visit each hotel and the time for serving the people quarantined in the hotel.
Let contain the indices of those hotels that have already been assigned to robot k to serve and let contain the indices of those unassigned hotels, which is initialized as . We use ok be the route containing the ordered hotels already assigned to robot k to serve, which is initialized as the index of k’s initial location {n + k}.
Then, the first hotel j* in the current to be assigned, its assigned robot k* and the serving sequence q* are determined by the TSTMCA as
where the operation inserts the index of hotel j at the qth position of robot k’s route ok, and t(ok) is the sum of the time for robot k to visit all the hotels in ok and the time spent on serving the people quarantined in the hotels. We will insert hotel j at the end of ok if q=|ok|+1. For each potential operation of inserting hotel j into the qth position of robot k’s current route ok, the robot’s total operation time needs to be checked to guarantee .
Then, the unassigned hotel set and robot k*’s current route are updated respectively as
The inserting and updating procedures Eqs. [10] and [11] continue until all the hotels in are assigned to the robots. The flowchart of TSTMCA is shown in Figure 2.
Travel time based marginal cost algorithm
For the objective function Eq. [2], the second term of the robots’ total operation time is the time to serve all the people quarantined in the n hotels, which is actually a fixed term as long as all of the people are served. As a result, in this section, we present the travel time based marginal cost algorithm (TTMCA), which assigns the hotel-serving tasks to the robots based on the travel time incurred for each robot to visit each newly-inserted hotel.
Let , and ok be the same as those defined for TSTMCA in the above section. Then, the first hotel j* in the current set to be assigned, its assigned robot k* and the serving sequence q* are chosen by the TTMCA as
where t'(ok) is the total travel time for robot k to visit all the hotels in ok. For each potential operation of inserting hotel j into the qth position of robot k’s current route ok, the robot’s total operation time needs to be checked to guarantee as TSTMCA. Then, Eq. [11] is used to update and . Afterwards, the inserting and updating procedures Eqs. [12] and [11] continue until all the hotels in are assigned to the robots. In Figure 2, inserting the unassigned hotel j* in at the q* th position of robot k* according to Eq. [12] leads to the flowchart of TTMCA.
Improvement strategies
After achieving an initial solution with the marginal cost based algorithms, two improvement strategies are designed to refine the current solution in this section based on the concept of Large Neighbourhood Search (31). The two strategies continuously remove one assigned task from a current solution and reassign this task if a better solution is found, which are called 1-opt improvement strategies.
As the time for a robot to serve the people quarantined in each hotel is a fixed term, removing a hotel-serving task from the current solution and then reassigning this task does not affect the amount of time for a robot to serve the people quarantined in the hotel. As a result, the 1-opt improvement strategies use the TTMCA Eq. [12] to reassign each removed task. Removing one assigned task and reassigning the task can be done sequentially or at the same time. We propose a decoupled 1-opt strategy and a coupled 1-opt strategy based on Eq. [12].
Decoupled 1-opt strategy
This section introduces the decoupled 1-opt strategy, which first removes a hotel-serving task from a current solution and then reassigns the hotel-serving task to the robots based on Eq. [12].
Let ok be the route containing the ordered hotels already assigned to robot k to serve in the current solution, and t'(ok) be the total travel time for robot k to visit all the hotels in ok as Eq. [12]. Let contain the indices of the hotels assigned to robot k in the current solution, which can be achieved based on ok. Then, the decoupled 1-opt strategy first calculates the potential maximum travel time that can be saved by removing the hotel-visiting task j* from the current route of robot k* as
where the operator removes the hotel-visiting task j from robot k’s current route ok. The removing operation Eq. [13] will save a total travel time as
Then, a trial operation is performed to reassign j* to robot k1* with the serving sequence q* as
The potential reassigning operation Eq. [15] will incur a total travel time cost as
Then, the removing operation Eq. [13] and the reassigning operation Eq. [15] for reassigning hotel j* will be indeed performed if the saved total travel time ts is greater than the incurred total travel time cost tc, i.e. ts>tc. It doesn’t stop until no more travel time can be saved by removing and reassigning tasks as Eqs. [13] and [15]. The decoupled 1-opt strategy improves the robots’ routes resulted from Eq. [12], which leads to the decoupled task assignment algorithm TTMCA(d) by integrating TTMCA with the decoupled 1-opt strategy. The flowchart of TTMCA(d) is shown in Figure 3.
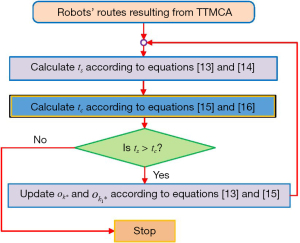
Coupled 1-opt strategy
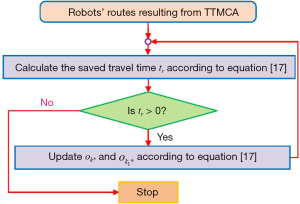
The coupled 1-opt strategy simultaneously performs the task removing and reassigning operations to check whether reassigning a hotel-visiting task can save some travel costs. At each improvement iteration, the coupled 1-opt strategy removes a hotel-visiting task j* from the current route of robot k*, and reassigns j* to robot k1* with the serving sequence q* to save the maximum travel time as
when the saved travel time is positive. The task removing and reassigning operation Eq. [17] goes on until there is no way to save more travel time on the trip.
The coupled 1-opt strategy improves the robots’ routes resulted from Eq. [12], which leads to the coupled task assignment algorithm TTMCA(c) by integrating TTMCA with the coupled 1-opt strategy. The flowchart of TTMCA(c) is shown in Figure 4.
Lower bound on the optimal solution
As the optimal solution to Eq. [2] is typically unknown, it is needed to investigate how to evaluate the quality of a sub-optimal solution. This section constructs a lower bound on the minimum total operation time for the robots to visit all the n hotels and to serve the people quarantined in the hotels, with the relaxation of each robot’s maximum operation time constraint.
Let be an undirected weighted robot-hotel graph whose vertices contain all the indices of the hotel locations and the robots’ initial positions. The weight of an undirected edge connecting a robot location vertex with a hotel location vertex is the Euclidean distance between them, which applies to each edge connecting two different hotel location vertices. Let zero be the weight of the edges between each pair of vertices representing robot locations. The Prim algorithm (13,32) is used to obtain a minimum spanning tree (MST) of that connects the index vertices of all the robots’ initial locations and hotel locations with the minimum total edge weight. Let fMST be the sum of all the edge weights of the MST and fo be the optimal value for the objective function [2].
Lemma 1: It holds that fMST≤ fo.
Proof: after relaxing the robots’ maximum operation time constraint, the task assignment problem Eq. [2] in essence is the OMTSP problem, where multiple dispersed robots need to visit a set of target locations with the minimum total travel distance with no requirement to return to their initial locations. As a result, the optimal value of the OMTSP provides a lower bound on the optimal solution of Eq. [2]. Since the optimal solution of the OMTSP is a special spanning tree of the undirected weighted robot-hotel graph where each hotel vertex connects at most one other hotel vertex, the sum of all the edge weights of the MST leads to a lower bound on the optimal solution of the OMTSP, which results in fMST≤ fo. Thus, the proof is complete.
Results
Simulation results
Numerical tests are first done in this section to test the performance of the designed algorithms compared with a greedy algorithm (GA) and the co-evolutionary multi-population genetic algorithm (CMGA) in (33). The GA assigns the hotel-serving tasks by always inserting the unassigned hotel location where the people quarantined in the hotel can be served the quickest at the end of the corresponding robot’s current route. For the CMGA, the gene operation parameters are set according to (33), which consists of five subpopulations, and the crossover rate and mutation rate are Pc =0.95 and Pm =0.1. All the experiments have been performed on an Intel Core i7 – 7500 U CPU 2.70 GHz with 8 GB RAM, and the algorithms are compiled by Matlab under Windows 10. The solution quality ratio r of each algorithm is quantified by
where f is the resulting objective value shown in Eq. [2], and fMST is the sum of all the edge weights of an MST of the undirected weighted robot-hotel graph achieved by the Prim algorithm (13,32). Since fMST≤ fo as shown in Lemma 1, a ratio r closer to 1 implies a better solution quality.
The algorithms are first tested using Monte Carlo simulation, in which people quarantined in n=30 dispersed hotels in a 10 km × 10 km area require m robots to serve them. The number of people quarantined in each of the n hotels is randomly generated, ranging from 30 to 100. It is assumed that an average fixed time of ot =30 s is needed for a robot to perform tasks such as body temperature assessment or oropharyngeal swabs for each person quarantined in the hotels, and the robots move at the unit speed of v=1 m/s. We assume that each robot’s maximum operation time is L=30,000 s, which is around 8 hours. Then, based on Eq. [1], the robots’ number is set as m∈{5,8,10}. For each scenario, 20 instances of the initial positions of the n hotels and the m robots are randomly distributed in the 10 km × 10 km area. For each instance, the genetic algorithm CMGA is performed 20 times to reduce its randomness, where the average objective value and the computational running time of the CMGA are used for the comparison. The robots’ average total operation time to serve all the people quarantined in the n=30 hotels and the corresponding average solution quality ratios r resulting from the algorithms are shown in Figure 5 and Figure 6, respectively.
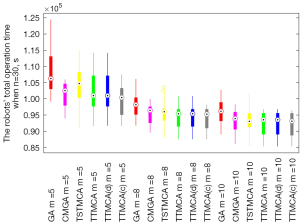
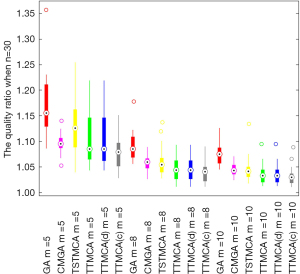
Firstly, Figure 5 shows that the robots’ average total operation time (s) to serve all the people quarantined in n=30 hotels, resulting from each algorithm, generally decreases when increasing the robots’ number m. This is because the robots are initially dispersed in the operation area, where the assignment of the n dispersed hotels can make a good use of the robots located at closer positions when more robots are available to be used. Secondly, Figure 5 shows the proposed algorithms TSTMCA and TTMCA are competitive compared with the CMGA, and are better than the GA, where the travel time based algorithm TTMCA is better than the TSTMCA. Furthermore, the integrated algorithms TTMCA(d) and TTMCA(c) are generally better than the TSTMCA and TTMCA, where TTMCA(c) has the best performance among the algorithms in all the scenarios as shown in Figure 5. The average solution quality ratios r of the algorithms shown in Figure 6 generally have the same changing trends as the robots’ average total operation time shown in Figure 5, which shows that the robots’ total operation times resulting from the proposed algorithms are generally within 1.15 times of the optimal value. This shows the satisfying performance of the designed algorithms.
Then, the algorithms are tested by Monte Carlo simulation with a larger problem size, where the people quarantined in n=90 dispersed hotels in a 10 km × 10 km area need to be served by m∈{16,18,20} robots. For each scenario, 20 instances of the initial positions of the n hotels and the m robots are randomly distributed in the 10 km × 10 km area. The number of people quarantined in each of the n hotels is randomly generated, ranging from 30 to 100. The robots’ moving speed and the maximum operation time are the same as when n=30. Due to the long computational running time of the CMGA when n=30 as shown in Table 1, the designed algorithms are compared with the GA when n=90. The robots’ average total operation time to serve all the people quarantined in n=90 hotels and the corresponding average solution quality ratios r resulting from the algorithms are shown in Figure 7 and Figure 8, respectively.
Table 1
| n | m | Algorithms’ average running time (ms) | |||||
|---|---|---|---|---|---|---|---|
| GA | CMGA | TSTMCA | TTMCA | TTMCA(d) | TTMCA(c) | ||
| 30 | 5 | 7.9305 | 26,016.2682 | 11.1637 | 8.5713 | 15.1322 | 21.2376 |
| 8 | 7.4494 | 29,799.6101 | 8.9224 | 7.4122 | 9.6264 | 8.5744 | |
| 10 | 7.2472 | 32,089.5982 | 8.0141 | 7.4525 | 9.1023 | 9.1222 | |
| 90 | 16 | 13.4218 | – | 31.7000 | 18.7472 | 20.1789 | 33.0617 |
| 18 | 13.4013 | – | 30.6582 | 19.4886 | 22.9485 | 39.7843 | |
| 20 | 14.1192 | – | 30.9932 | 20.0484 | 20.5622 | 33.0480 | |
CMGA, co-evolutionary multi-population genetic algorithm; n, number of hotels; m, number of robots; GA, greedy algorithm; TSTMCA, total serving time based marginal cost algorithm; TTMCA, travel time based marginal cost algorithm; TTMCA(d), algorithm integrating TTMCA with the decoupled 1-opt strategy; TTMCA(c), algorithm integrating TTMCA with the coupled 1-opt strategy.
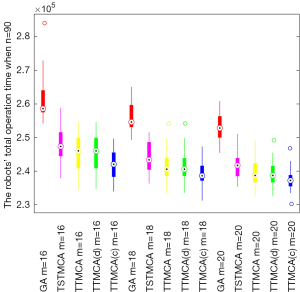
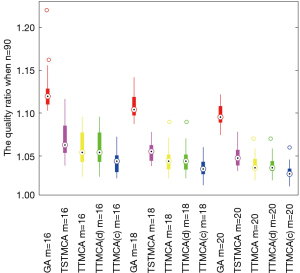
Figure 7 first shows that the robots’ average total operation time (s) to serve all the people quarantined in the n=90 hotels, resulting from each algorithm, increases compared with those when n=30 as shown in Figure 5, which is because more hotels need to be visited and the people quarantined in the hotels also need to be served. The other changing trends of the algorithms shown in Figure 7 are the same as those shown in Figure 5, where TTMCA(c) keeps the best performance among the algorithms in all the scenarios.
The algorithms’ average computational running times (ms) under each scenario of n=30 and n=90 are shown in Table 1. Table 1 first shows that the computational running times of the designed algorithms are competitive compared with the greedy method GA, which are pretty small in relation to the genetic algorithm CMGA. Secondly, the computational running times of the designed algorithms are increased to around 3 times from n=30 to n=90 as shown in Table 1, which shows the scalability of the designed algorithms. Thirdly, Table 1 shows that the better performance of the integrated algorithm TTMCA(c) among the designed algorithms comes at the cost of a longer running time.
Experimental results
In this section, the multi-robot task assignment experimental tests are carried out to verify the performance of the designed task assignment algorithm TTMCA(c) compared with the greedy algorithm GA and the co-evolutionary multi-population genetic algorithm CMGA in (33). In the experimental scenario, a fleet of m=3 dispersed autonomous mobile robots with initial location indexed by {n+1,…, n+m} needs to serve n=21 target locations (implying n hotels in the paper indexed by {1,…,n}) while trying to minimize the robots’ total operation time. The robot service time required by each target location ranges from 3 to 5 s, which corresponds to the time needed for body temperature assessment or oropharyngeal swabs for the persons quarantined in each associating hotel. The 21 target locations and the 3 Limo robots are randomly distributed in a 4 m × 5 m area.
Guided by each task assignment algorithm, the robots’ routes to serve the 21 target locations are respectively shown in Figures 9-11. The detailed movement of the robots can be found in the supplementary video (Video 1).



Discussion
First, the difference between the performance of the GA and that of the designed algorithms increases in Figure 7 compared with Figure 5, which shows the scalability of the designed algorithms. This conclusion is also verified by Figure 8, where the robots’ total operation time resulting from each proposed algorithm is generally within 1.1 times of the optimal value. This shows the satisfying performance of the designed algorithms.
Second, Figures 5-8 and Table 1 show that the TTMCA generally outperforms the TSTMCA on both the robots’ total operation time and the algorithms’ running time, which is interesting as both of them rely on the marginal cost to assign the hotel-serving tasks. This points out the importance of designing problem-specific assignment algorithms for similar task assignment problems.
Third, Figures 9-11 show that the target locations assigned to each robot by the TTMCA(c) are more balanced compared with the GA and the CMGA, where the total operation time of the robots guided by TTMCA(c) is respectively decreased by 17.7% and 11.4% in the comparison of the GA and the CMGA. This shows the satisfying performance of the designed task assignment algorithm TTMCA(c).
Conclusions
In this paper, we have studied the task assignment problem for multiple dispersed robots to efficiently serve the people quarantined in multiple hotels for body temperature assessment or oropharyngeal swabs missions while trying to minimize the robots’ total operation time. To evaluate the quality of an assignment solution, a lower bound on the robots’ total operation time to serve all the people has been constructed based on graph theory. Two marginal-cost-based task assignment algorithms are designed, and two 1-opt based improvement strategies are proposed to improve the current solution. Numerical experiments have shown that the proposed algorithms can obtain solutions that are closer to the optimal compared with the competitive genetic algorithm and a greedy algorithm. The proposed algorithms will be extended to online task assignment scenarios where new hotel-serving tasks might dynamically appear and require to be served. Additional research direction is to consider the case where the persons quarantined in each hotel require one robot to serve with a prescribed time-window constraint.
Acknowledgments
Funding: This work was supported by the National Natural Science Foundation of China (grant numbers 62003217, 62173234), and by the Shenzhen Natural Science Fund (the Stable Support Plan Program 20220809175803001).
Footnote
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at https://qims.amegroups.com/article/view/10.21037/qims-22-842/coif). The authors have no conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. No ethical approval or informed consent is required due to the nature of this study.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Fauci AS, Lane HC, Redfield RR. Covid-19 - Navigating the Uncharted. N Engl J Med 2020;382:1268-9. [Crossref] [PubMed]
- Agarwal S, Punn NS, Sonbhadra SK, Tanveer M, Nagabhushan P, Pandian K, Saxena P. Unleashing the power of disruptive and emerging technologies amid COVID-19: A detailed review. arXiv preprint arXiv:2005.11507 2020:1-60.
- Bogue R. Robots in a contagious world. Industrial Robot 2020;47:637-42. [Crossref]
- Available online: http://www.manbu.cc/index.php?id=2489 (accessed on 16 November 2022).
- Yang GZ. J Nelson B, Murphy RR, Choset H, Christensen H, H Collins S, Dario P, Goldberg K, Ikuta K, Jacobstein N, Kragic D, Taylor RH, McNutt M. Combating COVID-19-The role of robotics in managing public health and infectious diseases. Sci Robot 2020;5:eabb5589. [Crossref] [PubMed]
- Sahu B, Das PK, Kabat MR, Kumar R. Prevention of Covid-19 affected patient using multi robot cooperation and Q-learning approach: a solution. Qual Quant 2022;56:793-821. [Crossref] [PubMed]
- Alsamhi SH, Lee B. Blockchain-Empowered Multi-Robot Collaboration to Fight COVID-19 and Future Pandemics. IEEE Access 2021;9:44173-97.
- Alsamhi SH, Lee B, Guizani M, Kumar N, Qiao Y, Liu X. Blockchain for decentralized multi-drone to combat COVID-19 and future pandemics: framework and proposed solutions. Transactions on Emerging Telecommunications Technologies 2021;32:e4255. [Crossref]
- Korsah GA, Stentz A, Dias MB. A comprehensive taxonomy for multi-robot task allocation. The International Journal of Robotics Research 2013;32:1495-512. [Crossref]
- Smith SL, Bullo F. Monotonic target assignment for robotic networks. IEEE Transactions on Automatic Control 2009;54:2042-57. [Crossref]
- Bai X, Cao M, Yan W. Event- and time-triggered dynamic task assignments for multiple vehicles. Autonomous Robots 2020;44:877-88. [Crossref]
- Yu J, Chung SJ, Voulgaris PG. Target assignment in robotic networks: Distance optimality guar antees and hierarchical strategies. IEEE Transactions on Automatic Control 2015;60:327-41. [Crossref]
- Bai X, Yan W, Ge SS. Distributed Task Assignment for Multiple Robots Under Limited Communication Range. IEEE Transactions on Systems, Man, and Cybernetics: Systems 2022;52:4259-71. [Crossref]
- Toth P, Vigo D. Vehicle routing: problems, methods, and applications. vol. 18. Society for Indus trial and Applied Mathematics, 2014.
- Prins C. A simple and effective evolutionary algorithm for the vehicle routing problem. Computers & Operations Research 2004;31:1985-2002. [Crossref]
- Kuo Y. Using simulated annealing to minimize fuel consumption for the time-dependent vehicle routing problem. Computers & Industrial Engineering 2010;59:157-65. [Crossref]
- Escobar JW, Linfati R, Toth P, Baldoquin MG. A hybrid granular tabu search algorithm for the multi-depot vehicle routing problem. Journal of Heuristics 2014;20:483-509. [Crossref]
- Wang L, Lu J. A memetic algorithm with competition for the capacitated green vehicle routing problem. IEEE/CAA Journal of Automatica Sinica 2019;6:516-26.
- Lagoudakis MG, Berhault M, Koenig S, Keskinocak P, Kleywegt AJ. Simple auctions with performance guarantees for multi-robot task allocation. In: 2004 IEEE/RSJ International Conference on Intelligent Robots and Systems. IEEE; 2004;1:698-705.
- Bai X, Yan W, Cao M, Xue D. Distributed multi-vehicle task assignment in a time-invariant drift field with obstacles. IET Control Theory & Applications 2019;13:2886-93. [Crossref]
- Choi HL, Brunet L, How JP. Consensus-based decentralized auctions for robust task allocation. IEEE Transactions on Robotics 2009;25:912-26. [Crossref]
- Wang J, Sun Y, Zhang Z, Gao S. Solving multitrip pickup and delivery problem with time windows and manpower planning using multiobjective algorithms. IEEE/CAA Journal of Automatica Sinica 2020;7:1134-53.
- Shima T, Rasmussen SJ, Sparks AG, Passino KM. Multiple task assignments for cooperating uninhabited aerial vehicles using genetic algorithms. Computers & Operations Research 2006;33:3252-69. [Crossref]
- Edison E, Shima T. Integrated task assignment and path optimization for cooperating uninhabited aerial vehicles using genetic algorithms. Computers & Operations Research 2011;38:340-56. [Crossref]
- Sahal R, Alsamhi SH, Brown KN, O'Shea D, Alouffi B. Blockchain-Based Digital Twins Collaboration for Smart Pandemic Alerting: Decentralized COVID-19 Pandemic Alerting Use Case. Comput Intell Neurosci 2022;2022:7786441. [Crossref] [PubMed]
- Aggarwal A, Chakradar M, Bhatia MS, Kumar M, Stephan T, Gupta SK, Alsamhi SH, Al-Dois H. COVID-19 Risk Prediction for Diabetic Patients Using Fuzzy Inference System and Machine Learning Approaches. J Healthc Eng 2022;2022:4096950. [Crossref] [PubMed]
- Alouffi B, Alharbi A, Sahal R, Saleh H. An Optimized Hybrid Deep Learning Model to Detect COVID-19 Misleading Information. Comput Intell Neurosci 2021;2021:9615034. [Crossref] [PubMed]
- Sahal R, Alsamhi SH, Brown KN, O’Shea D, McCarthy C, Guizani M. Blockchain-empowered digital twins collaboration: smart transportation use case. Machines 2021;9:193. [Crossref]
- Bektas T. The multiple traveling salesman problem: an overview of formulations and solution procedures. Omega 2006;34:209-19. [Crossref]
- Bai X, Yan W, Cao M. Clustering-based algorithms for multivehicle task assignment in a time-invariant drift field. IEEE Robotics and Automation Letters 2017;2:2166-73. [Crossref]
- Shaw P. Using constraint programming and local search methods to solve vehicle routing problems. In: International Conference on Principles and Practice of Constraint Programming. Springer, 1998;1:417-31.
- Papadimitriou CH, Steiglitz K. Combinatorial optimization: algorithms and complexity. Courier Corporation, 1998.
- Bai X, Yan W, Ge SS, Cao M. An integrated multi-population genetic algorithm for multi-vehicle task assignment in a drift field. Information Sciences 2018;453:227-38. [Crossref]



