Errors in quantitative T1rho imaging and the correction methods
Introduction
T1rho is the time constant of spin-lattice relaxation in rotating frame, which characterizes relaxation of magnetization under influence of a radiofrequency (RF) field. Conventional spin-lattice relaxation (T1) is particularly sensitive to processes in the lattice which occurs at high frequency near Larmor frequency (i.e., in MHz range). In contrast, T1rho is discovered to be sensitive to lattice processes occurring at much lower frequency close to the Rabi frequency of the spin-lock RF pulse, which typically is in the range of a few hundred hertz. Since slow motion in lattice is associated with macromolecular, such as proteins, T1rho is anticipated to be useful for assessment of the properties of macromolecular environment in tissue which conventional methods cannot offer.
Quantitative T1rho imaging has been investigated for many clinical applications (1-25). One of the greatest challenges of T1rho quantification in routine clinical practice is its robustness. A number of sources can cause quantification errors. A great deal of effort has been spent to develop methods to compensate these errors. It is the purpose of this article to review and discuss quantification errors in T1rho and the correction methods which are currently available.
The basics of T1rho
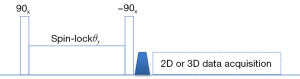
T1rho is often measured by the spin-lock technique described by Redfield (26). T1rho preparation (prep) typically starts with a 90-degree RF pulse (tip-down RF) to flip magnetization into transverse plane. An on-resonance continuous wave RF pulse (termed spin-lock RF pulse) is then applied in parallel to the magnetization, which causes the magnetization to process around it and appears to be “spin-locked”. During the time of spin-lock (TSL), the magnetization relaxes under the influence of the spin-lock RF pulse with time constant of T1rho instead of conventional T2. After the spin-lock process, the magnetization is flipped back into longitudinal direction by another 90-degree RF pulse (tip-up RF). A crusher is then followed to dephase the residual signal in transverse plane. The magnetization after such T1rho prep can be expressed as:

where I0 is a constant which is independent of TSL.
Various 2D or 3D data acquisitions methods can be used after T1rho prep to collect imaging data. To quantify T1rho value, data sets with different TSL are acquired and then fitted to Eq. [1]. Fat suppression is usually applied to avoid significant banding artifacts since spin-lock is susceptible to chemical shift of fat. Figure 1 shows a schematic diagram of conventional continues wave T1rho prep and the imaging data acquisition.
Compensation of B1 RF inhomogeneity
The conventional T1rho prep method shown in Figure 1 is susceptible to B1 RF inhomogeneity. At the presence of B1 RF inhomogeneity, the expected 90-degree tip-down RF pulse flips magnetization to an orientation deviated from transverse plane. Consequently, the magnetization rotates at an angle around the spin-lock RF pulse during TSL. After the tip-up RF pulse, the longitudinal magnetization becomes a complicated function of TSL shown below:
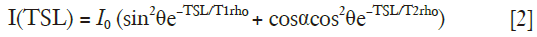
where θ is the actual flip angle of the tip-up/tip-down RF pulse, T2rho is the magnetization decay rate in the plane perpendicular to the spin-locking RF pulse, and α is the total flip angle during spin locking which is proportional to TSL. The presence of cosα term results in spatial modulation of signal which manifests as banding artifacts in acquired images.
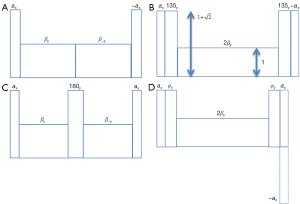
By reversing the amplitude or phase of the second half of the spin-locking RF pulse, the net flip angle during spin lock becomes zero. Consequently, the cosα term is canceled out in Eq. [2]. This is the rotary echo approach proposed by Charagundla et al. (27), which is commonly used to address B1 RF inhomogeneity effect in T1rho imaging. Figure 2A shows a schematic diagram of this method. It can be shown that with rotary echo approach, the longitudinal magnetization after T1rho prep is:
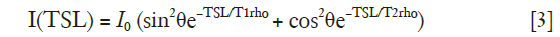
Note that compared to the conventional T1rho prep, cosα term is eliminated using rotary echo method. However, the T2rho term remains, which results in quantification error if mono-exponential relaxation model of Eq. [1] is used to obtain T1rho value.
It was reported that B1 inhomogeneity effect on continuous wave T1rho prep could be fully compensated by a phase cycling method (28). In this method, two data sets are acquired with opposite phase of the tip-up RF pulse. These two data sets are then subtracted from each other. The longitudinal magnetization after subtraction is:
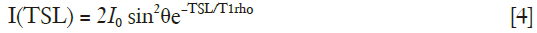
Note compared to the rotary echo approach, the second term in Eq. [3] is completely eliminated after phase cycling. Therefore, the mono-exponential decay model depicted by Eq. [1] can be used to fit T1rho accurately after phase cycling without being compromised by B1 RF inhomogeneity.
The apparent downside of the phase cycling method is it doubles scan time, even though the signal-to-noise ratio (SNR) is elevated to a level similar to that of 2 NEX acquisitions. For certain T1rho imaging pulse sequences which requires phase cycling to remove T1 relaxation effect during data acquisition, such as 3D magnetization-prepared angle-modulated partitioned k-space spoiled gradient echo snapshots (MAPSS) (29), there is no scan time penalty to use this method for B1 inhomogeneity compensation.
Adiabatic RF pulses are commonly used to address B1 RF inhomogeneity in MRI system. Researchers have used adiabatic half-passage (AHP) pulses to address B1 inhomogeneity effect on continuous wave T1rho prep (6,30). In these methods, AHP pulses are used to generate uniform 90-degree excitation, followed by continuous wave spin-lock RF pulses. The magnetization is either flipped back to longitudinal direction by another AHP pulse followed with imaging data acquisition (6), or directly followed with imaging module for data collection (30).
Compensation of B0 field inhomogeneity
The presence of B0 field inhomogeneity can cause image artifacts to T1rho-weighted imaging and T1rho quantification error. Shimming is highly recommended for T1rho imaging. However, shimming alone usually cannot eliminate off-resonance effect.
When there is off-resonance, the effective magnetic field in the rotating frame during spin-lock is the combination of B1 RF and B0 field. The orientation of this effective magnetic field with respect to transverse plane is:

Note this angle diminishes when the amplitude of B1 increases. Therefore, a simple way to overcome the adversary effect from off-resonance during spin-lock is to increase the amplitude of the spin-lock RF pulse. However, the maximum RF amplitude is limited by the power of RF amplifier. High amplitude combined with long duration of spin-lock RF also leads to elevated special absorption rate (SAR). The situation is worsened when body RF transmitter rather than local transceiver coil is used.
Dixon et al. (2) reported a method to compensate off-resonance effect during spin-lock by using composite RF pulses. In this approach, a 135-degree RF pulse with phase same as spin-lock RF pulse is inserted both before and after spin-lock, as shown in Figure 2B. The amplitude of the composite RF pulses satisfies:

where 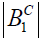 and
and 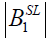 are the amplitude of the composite RF pulse and the spin-lock RF pulse, respectively. For spin-lock RF pulse at 500 Hz, which is commonly used in practice, however, the amplitude of the composite RF pulses specified by Eq. [6] is approximately 1.2 kHz, which may not be practical to use since it is close to the power limit of RF amplifier equipped in a modern clinical scanner.
are the amplitude of the composite RF pulse and the spin-lock RF pulse, respectively. For spin-lock RF pulse at 500 Hz, which is commonly used in practice, however, the amplitude of the composite RF pulses specified by Eq. [6] is approximately 1.2 kHz, which may not be practical to use since it is close to the power limit of RF amplifier equipped in a modern clinical scanner.
Simultaneous compensation of B1 RF and B0 field inhomogeneity
The methods described in previous sections are aimed for compensation of either B1 RF inhomogeneity or B0 field inhomogeneity. The combination of both of them can compromise the effectiveness of these methods and methods which can address B1 RF and B0 inhomogeneity effect simultaneously are needed.
One method with aim to address this issue is proposed by Zeng et al. (31). In this method, a 180-degree refocusing RF pulse with the same phase as spin-lock RF pulse is inserted in the middle of the rotary echo RF pulse, which is used to compensate off-resonance effect accrued during spin-lock. However, it is shown that this approach can be sensitive to B1 RF inhomogeneity (32). Incomplete compensation can arise when the flip angle of tip-down/up RF pulse is not exactly 90 degree and/or the flip angle of the refocusing pulse is not exactly 180 degree.
Witschey et al. (32) discovered that by reversing the phase of the tip-down RF pulse in the method reported by Zeng et al. (31), the same T1rho prep becomes insensitive to the flip angle of tip-down/up RF pulses. A schematic diagram of this approach is shown in Figure 2C. The effectiveness of this method for simultaneous compensation of B1 and B0 inhomogeneity, however, still can be compromised if the flip angle of the refocusing RF pulse is not 180 degree. This imperfection may be mitigated by increasing the amplitude of the refocusing pulse or using B1 insensitive 180-degree refocusing pulses (32).
By combining the composite RF pulse reported by Dixon et al. (2) with phase cycling method, we can also achieve simultaneous compensation of B1 and B0 field inhomogeneity for continues wave T1rho prep (28). A schematic diagram of this approach is shown in Figure 2D. It is reported that this method is effective when the amplitude of the composite RF pulse deviates from that specified by Eq. [6], therefore insensitive to B1 inhomogeneity effect (28). The downside of this method, however, is the prolonged scan time.
Spin-lock using Adiabatic RF pulse with insensitivity to B1 RF and B0 field inhomogeneity
Conventionally spin-lock is implemented by continuous wave RF pulses. The methods we described in previous sections are developed to improve the robustness of this type of spin-lock approach under the presence of B1 RF and B0 field inhomogeneity. A different way to achieve spin-lock is to use adiabatic RF pulses (33-35). The hyperbolic secant RF pulses used in these methods for spin-lock are inherently insensitive to B1 RF and B0 field inhomogeneity (34-40). In the studies reported in references (34-40), a train of adiabatic full-passage (AFP) hyperbolic secant RF pulses are applied to create spin-lock contrast. During the application of these pulses, both amplitude and frequency are modulated, which leads to variation of amplitude and orientation of effective field in time. When the adiabatic condition is satisfied, namely, the orientation of the effective magnetic field changes slower than the rotation of magnetization about this effective field (41), which can be achieved by sufficiently high B1 amplitude or a slow frequency sweep, the spins are spin-locked along the effective field and decay at a time varying T1rho rate. By fitting the images collected with different levels of adiabatic T1rho contrast to a mono-exponential decay model, the average T1rho relaxation rate is measured over the pulse duration. The measured adiabatic T1rho value varies when different types of adiabatic RF pulses with different amplitude and frequency modulation is used. Recently, a type of gradient modulated adiabatic pulses is reported for adiabatic T1rho imaging which can achieve reduced artifacts from B1 and B0 field inhomogeneity, and the same time reduced power deposition, short scan time, and slice selectivity (42).
Compared to continuous waveform spin-lock, T1rho varies during the adiabatic spin-lock since the amplitude and frequency of the pulse is modulated during the time course. Consequently, the measured T1rho is an average value over the duration of adiabatic pulse. The clinical use of T1rho quantification using adiabatic spin-lock is not as well understood as that using continuous waveform spin-lock, and therefore further clinical study of this method is needed.
Errors from data acquisition and the correction methods
There is a multitude of imaging sequences which can be used to collect data after T1rho contrast is imparted to the magnetization. The imaging sequence usually is put after T1rho prep, as shown in Figure 1. With inclusion of particular imaging sequence, the whole pulse sequence of T1rho imaging inherits its sensitivity to system imperfection, i.e., Fast (Turbo) Spin Echo is sensitive to factors causing the violation of CPMG condition. In addition, the signal evolution during imaging sequence may complicate the quantification of T1rho and care is needed to address these issues.
Borthakur et al. (43) reported a 3D T1rho imaging approach based on steady state spoiled gradient echo acquisition. Only one phase encoding line is acquired for every T1rho prep in this approach. The signal at steady state is expressed by the following equation which is used to fit the T1rho value:
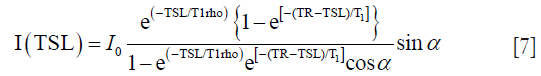
where α is the flip angle, and TR is the repetition time. Eq. [7] indicates that erroneous value of α due to B1 inhomogeneity and inaccurate prior knowledge of T1 can lead to T1rho quantification error in this method.
Li et al. (29) reported a 3D quantitative T1rho imaging method termed MAPSS which is based on segmented SPGR acquisition. The data is acquired during the transient signal evolution toward steady state. A primary concern of direct use of segmented SPGR acquisition for T1rho quantification is that T1 relaxation during imaging data acquisition can degrade T1rho contrast. As shown by Li et al. (29), the transverse magnetization after the nth RF pulse during SPGR readout can be expressed as:
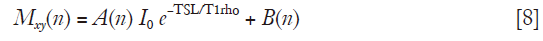
where A(n) and B(n) are complicated functions of relaxation parameters and pulse sequence parameters. The expression of these two terms can be found in reference (29). Note the term B(n) in Eq. [8] is an additive term and impacts quantification accuracy if not corrected. To address this issue, Li et al. (29) proposed to acquire two data sets with opposite phase of the tip-up RF pulse, and then subtract them from each other, which yield:

Note the magnitude image after subtraction can be fitted to a mono-exponential decay model to calculate T1rho without error.
For multi-slice 2D imaging, if multiple slices are acquired after one T1rho prep, T1 relaxation during the time course after T1rho prep can lead to quantification error when Eq. [1] is used as the relaxation model (44), in a similar manner as in MAPSS. The same phase cycling method has been used to address this issue in multi-slice quantitative T1rho imaging (44).
Fast (or Turbo) Spin Echo (FSE or TSE) with long echo train has also been reported for quantitative T1rho imaging (45,46). In FSE (TSE) acquisition, when the CPMG condition is met and the crusher gradient is sufficient so that FID is eliminated, T1 recovery during the readout is eliminated. The point spread functions for all TSL values are identical and relative image intensity between images acquired with different TSL values depends only on T1rho exponential decay during spin lock. Therefore, no phase cycling is needed to address T1 relaxation effect during long readout of FSE, which makes FSE based T1rho imaging highly SNR efficient. Compared to 3D gradient echo acquisition, the downside of 3D FSE acquisition, however, is increased echo time which is unfavorable when imaging tissue with relative short T2, increased sensitivity to eddy current, and potential blurring when long echo train is used (46).
Balanced gradient echo sequence (47) can also be used for fast quantitative imaging. Instead of acquiring imaging data in steady state after a number of dummy pulses, signal has to be acquired during transient stage in this approach. Otherwise, contrast loss during the transient decay can result in elevated T1rho estimation (47). Collecting date during transient stage in balanced gradient echo sequence can cause image blurring. The authors proposed to design a filter applied in k-space to address this issue (47).
Errors from insufficient SNR and the correction methods
SNR plays a critical role in quantitative imaging. There is increasing interest in acquiring parametric map with high resolution and/or fast scan, which inevitably costs SNR. Care must be used to avoid quantification error from insufficient SNR.
In MRI system, noise follows Gaussian distribution with zero mean in frequency domain. The commonly used linear regression approach, which is based on weighted least square fit of the logarithm of the magnitude image, has advantage of simplicity and fast computation time. However, the logarithm transform of the image causes the noise distribution no longer to be normal, which violates the assumption underneath the least square fit. The quantification using this approach is still approximately accurate when SNR is high, but large bias appears when SNR is low (48). Non-linear fit of Eq. [1] without applying logarithm transform (49,50) may improve quantification accuracy. However, large bias remains since the noise in magnitude image can deviate from Gaussian distribution significantly with a non-zero mean when SNR is low (49,50).
Truncation method is used in some studies to address the SNR issue. In this method, data sets acquired with long TSL are discarded if they are regarded with insufficient SNR. However, such practice is not preferred since quantification accuracy requires the entire decay curve, including long TSL, is sampled (51).
A common practice of quantitative imaging is to measure parameter within a ROI instead of on one single pixel. SNR can be greatly increased by averaging signal within ROI. For such practice, it is preferred to take average of ROI within a complex image instead of magnitude image to avoid significant error due to non-zero mean of noise in magnitude image at low SNR. The downside of the ROI approach is reduced resolution of acquired parametric map.
A modification of the relaxation model has been investigated to address noise issue in tissue parameter quantification. Instead of fitting using Eq. [1], it is proposed by Mosher (52) to fit the magnitude image using the following equation:

where C is an unknown constant. However, it is reported that, even though this model improves the accuracy of relaxation parameter estimation at low range, it prone to underestimate relaxation parameter, especially for long relaxation (49).
Compared to Eq. [10], a more accurate model to include noise in magnitude image for tissue parameter quantification is reported by Miller and Joseph (53). For a single receiver system, without partial Fourier, parallel imaging, and other advanced reconstruction, Miller and Joseph discovered that the mean of the square of magnitude image can be expressed as (53):

where Itrue is the image in absence of noise, and σ is the standard deviation of noise in either real or imagery channel. Therefore, we can subtract noise 2σ2 from the mean of square of image intensity before fitting the data to a mono-exponential decay model (53). This approach was shown to be more accurate than linear or non-linear fit using Eq. [1] (49).
For single receiver system, the magnitude image follows Rician distribution (54-56). Raya et al. (49) calculated the analytical solution of the mean of image intensity (termed noise corrected exponential function), and then estimate relaxation parameter by non-linear fitting of magnitude image to this noise corrected exponential function. They demonstrated that such fit method results in precisions comparable to the best achievable precisions determined by Cramer-Rao lower bound.
One limitation of these noise-corrected approaches is that they are only applicable for single receiver system. Hardy and Andersen (50) established a noise-corrected approach for phased array system. Ignore noise correlation between receivers in phased array and assume they are statistically independent; the magnitude image of standard square-root-of-sum-of-square reconstruction follows non-central chi distribution (57). Hardy and Andersen proposed a lookup table approach where the difference between the magnitude image and the true image caused by noise is pre-calculated offline based on the analytical expression of non-central chi distribution. These values are stored in a lookup table and the corresponding amount of correction for particular imaging case is read from the table and applied to the magnitude image for correction. A mono-exponential decay model based on non-linear least square fit is then applied to the corrected image to estimate relaxation parameter.
Another approach which is applicable for parameter quantification using phased array is maximum likelihood method (48). This method derives the best estimate of relaxation parameter by maximizing the joint distribution of magnitude image at different TSL (48,50). Hardy and Andersen show that the maximum likelihood approach and the noise-corrected lookup table approach provide very close estimation, but the great difference in computational complexity and computational time makes the lookup table approach a favorable choice (50).
Summary
The spin-lock technique used to generate T1rho contrast provides a mechanism to probe into macromolecular environment which conventional imaging methods cannot offer. Consequently, T1rho quantification has potential in many clinical applications. However, despite the promising outcomes of the published studies, it remains challenging to achieve robust and accurate T1rho quantification in routine clinical practice. In this article, the major sources which can cause errors to T1rho quantification and the correction methods are reviewed. The review is focused on error sources including system imperfections, inappropriate pulse sequence design, and insufficient SNR. For certain tissue types, additional factors which may confound T1rho quantification can arise due to inherent tissue properties. For example, magic angle effect (58,59) and multiple relaxation components (60-62) are commonly observed when imaging cartilage and fibrocartilage. Review of these confounding factors for relaxometry due to inherent tissue properties is not included in this article.
Acknowledgements
The author would like to thank Dr. Yì-Xiáng J. Wáng for proofreading the article and reviewers for reviewing the article.
Footnote
Conflicts of Interest: The author has no conflicts of interest to declare.
References
- Santyr GE, Henkelman RM, Bronskill MJ. Spin locking for magnetic resonance imaging with application to human breast. Magn Reson Med 1989;12:25-37. [PubMed]
- Dixon WT, Oshinski JN, Trudeau JD, Arnold BC, Pettigrew RI. Myocardial suppression in vivo by spin locking with composite pulses. Magn Reson Med 1996;36:90-4. [PubMed]
- Aronen HJ, Ramadan UA, Peltonen TK, Markkola AT, Tanttu JI, Jääskeläinen J, Häkkinen AM, Sepponen R. 3D spin-lock imaging of human gliomas. Magn Reson Imaging 1999;17:1001-10. [PubMed]
- Regatte RR, Akella SV, Borthakur A, Kneeland JB, Reddy R. Proteoglycan depletion-induced changes in transverse relaxation maps of cartilage: comparison of T2 and T1rho. Acad Radiol 2002;9:1388-94. [PubMed]
- Regatte RR, Akella SV, Borthakur A, Reddy R. Proton spin-lock ratio imaging for quantitation of glycosaminoglycans in articular cartilage. J Magn Reson Imaging 2003;17:114-21. [PubMed]
- Gröhn OH, Mäkelä HI, Lukkarinen JA, DelaBarre L, Lin J, Garwood M, Kauppinen RA. On- and off-resonance T(1rho) MRI in acute cerebral ischemia of the rat. Magn Reson Med 2003;49:172-6. [PubMed]
- Borthakur A, Wheaton AJ, Gougoutas AJ, Akella SV, Regatte RR, Charagundla SR, Reddy R. In vivo measurement of T1rho dispersion in the human brain at 1.5 tesla. J Magn Reson Imaging 2004;19:403-9. [PubMed]
- Muthupillai R, Flamm SD, Wilson JM, Pettigrew RI, Dixon WT. Acute myocardial infarction: tissue characterization with T1rho-weighted MR imaging--initial experience. Radiology 2004;232:606-10. [PubMed]
- Regatte RR, Akella SV, Wheaton AJ, Lech G, Borthakur A, Kneeland JB, Reddy R. 3D-T1rho-relaxation mapping of articular cartilage: in vivo assessment of early degenerative changes in symptomatic osteoarthritic subjects. Acad Radiol 2004;11:741-9. [PubMed]
- Johannessen W, Auerbach JD, Wheaton AJ, Kurji A, Borthakur A, Reddy R, Elliott DM. Assessment of human disc degeneration and proteoglycan content using T1rho-weighted magnetic resonance imaging. Spine (Phila Pa 1976) 2006;31:1253-7. [PubMed]
- Regatte RR, Akella SV, Lonner JH, Kneeland JB, Reddy R. T1rho relaxation mapping in human osteoarthritis (OA) cartilage: comparison of T1rho with T2. J Magn Reson Imaging 2006;23:547-53. [PubMed]
- Blumenkrantz G, Li X, Han ET, Newitt DC, Crane JC, Link TM, Majumdar S. A feasibility study of in vivo T1rho imaging of the intervertebral disc. Magn Reson Imaging 2006;24:1001-7. [PubMed]
- Auerbach JD, Johannessen W, Borthakur A, Wheaton AJ, Dolinskas CA, Balderston RA, Reddy R, Elliott DM. In vivo quantification of human lumbar disc degeneration using T(1rho)-weighted magnetic resonance imaging. Eur Spine J 2006;15 Suppl 3:S338-44. [PubMed]
- Lozano J, Li X, Link TM, Safran M, Majumdar S, Ma CB. Detection of posttraumatic cartilage injury using quantitative T1rho magnetic resonance imaging. A report of two cases with arthroscopic findings. J Bone Joint Surg Am 2006;88:1349-52. [PubMed]
- Li X, Benjamin Ma C, Link TM, Castillo DD, Blumenkrantz G, Lozano J, Carballido-Gamio J, Ries M, Majumdar S. In vivo T(1rho) and T(2) mapping of articular cartilage in osteoarthritis of the knee using 3 T MRI. Osteoarthritis Cartilage 2007;15:789-97. [PubMed]
- Borthakur A, Sochor M, Davatzikos C, Trojanowski JQ, Clark CM. T1rho MRI of Alzheimer's disease. Neuroimage 2008;41:1199-205. [PubMed]
- Li X, Pai A, Blumenkrantz G, Carballido-Gamio J, Link T, Ma B, Ries M, Majumdar S. Spatial distribution and relationship of T1rho and T2 relaxation times in knee cartilage with osteoarthritis. Magn Reson Med 2009;61:1310-8. [PubMed]
- Du J, Carl M, Diaz E, Takahashi A, Han E, Szeverenyi NM, Chung CB, Bydder GM. Ultrashort TE T1rho (UTE T1rho) imaging of the Achilles tendon and meniscus. Magn Reson Med 2010;64:834-42. [PubMed]
- Haris M, Singh A, Cai K, Davatzikos C, Trojanowski JQ, Melhem ER, Clark CM, Borthakur A. T1rho (T1ρ) MR imaging in Alzheimer’s disease and Parkinson's disease with and without dementia. J Neurol 2011;258:380-5. [PubMed]
- Haris M, McArdle E, Fenty M, Singh A, Davatzikos C, Trojanowski JQ, Melhem ER, Clark CM, Borthakur A. Early marker for Alzheimer’s disease: hippocampus T1rho (T(1rho)) estimation. J Magn Reson Imaging 2009;29:1008-12. [PubMed]
- Wang YX, Yuan J, Chu ES, Go MY, Huang H, Ahuja AT, Sung JJ, Yu J. T1rho MR imaging is sensitive to evaluate liver fibrosis: an experimental study in a rat biliary duct ligation model. Radiology 2011;259:712-9. [PubMed]
- Wang YX, Zhao F, Griffith JF, Mok GS, Leung JC, Ahuja AT, Yuan J. T1rho and T2 relaxation times for lumbar disc degeneration: an in vivo comparative study at 3.0-Tesla MRI. Eur Radiol 2013;23:228-34. [PubMed]
- Witschey WR, Zsido GA, Koomalsingh K, Kondo N, Minakawa M, Shuto T, McGarvey JR, Levack MM, Contijoch F, Pilla JJ, Gorman JH 3rd, Gorman RC. In vivo chronic myocardial infarction characterization by spin locked cardiovascular magnetic resonance. J Cardiovasc Magn Reson 2012;14:37. [PubMed]
- Rauscher I, Eiber M, Ganter C, Martirosian P, Safi W, Umgelter A, Rummeny EJ, Holzapfel K. Evaluation of T1ρ as a potential MR biomarker for liver cirrhosis: comparison of healthy control subjects and patients with liver cirrhosis. Eur J Radiol 2014;83:900-4. [PubMed]
- Allkemper T, Sagmeister F, Cicinnati V, Beckebaum S, Kooijman H, Kanthak C, Stehling C, Heindel W. Evaluation of fibrotic liver disease with whole-liver T1ρ MR imaging: a feasibility study at 1.5 T. Radiology 2014;271:408-15. [PubMed]
- Redfield AG. Nuclear magnetic resonance saturation and rotary saturation in solids. Phys Rev 1955;98:1787-1809.
- Charagundla SR, Borthakur A, Leigh JS, Reddy R. Artifacts in T(1rho)-weighted imaging: correction with a self-compensating spin-locking pulse. J Magn Reson 2003;162:113-21. [PubMed]
- Chen W, Takahashi A, Han E. Quantitative T(1)(ρ) imaging using phase cycling for B0 and B1 field inhomogeneity compensation. Magn Reson Imaging 2011;29:608-19. [PubMed]
- Li X, Han ET, Busse RF, Majumdar S. In vivo T(1rho) mapping in cartilage using 3D magnetization-prepared angle-modulated partitioned k-space spoiled gradient echo snapshots (3D MAPSS). Magn Reson Med 2008;59:298-307. [PubMed]
- Gröhn HI, Michaeli S, Garwood M, Kauppinen RA, Gröhn OH. Quantitative T(1rho) and adiabatic Carr-Purcell T2 magnetic resonance imaging of human occipital lobe at 4 T. Magn Reson Med 2005;54:14-9. [PubMed]
- Zeng H, Daniel G, Gochberg C, Zhao Y, Avison M, Gore JC. A composite spin-lock pulse for ΔB0 + B1 insensitive T1rho measurement. Proc. Soc. Magn. Reson. Med., ISMRM Annual Meeting. Seattle, Washington, USA, 2006:2356.
- Witschey WR 2nd, Borthakur A, Elliott MA, Mellon E, Niyogi S, Wallman DJ, Wang C, Reddy R. Artifacts in T1 rho-weighted imaging: compensation for B(1) and B(0) field imperfections. J Magn Reson 2007;186:75-85. [PubMed]
- Taheri S, Sood R. Spin-lock MRI with amplitude- and phase-modulated adiabatic waveforms: an MR simulation study. Magn Reson Imaging 2006;24:51-9. [PubMed]
- Michaeli S, Sorce DJ, Springer CS Jr, Ugurbil K, Garwood M. T1rho MRI contrast in the human brain: modulation of the longitudinal rotating frame relaxation shutter-speed during an adiabatic RF pulse. J Magn Reson 2006;181:135-47. [PubMed]
- Mangia S, Liimatainen T, Garwood M, Michaeli S. Rotating frame relaxation during adiabatic pulses vs. conventional spin lock: simulations and experimental results at 4 T. Magn Reson Imaging 2009;27:1074-87. [PubMed]
- Jokivarsi KT, Niskanen JP, Michaeli S, Gröhn HI, Garwood M, Kauppinen RA, Gröhn OH. Quantitative assessment of water pools by T 1 rho and T 2 rho MRI in acute cerebral ischemia of the rat. J Cereb Blood Flow Metab 2009;29:206-16. [PubMed]
- Ellermann J, Ling W, Nissi MJ, Arendt E, Carlson CS, Garwood M, Michaeli S, Mangia S. MRI rotating frame relaxation measurements for articular cartilage assessment. Magn Reson Imaging 2013;31:1537-43. [PubMed]
- Rautiainen J, Nissi MJ, Liimatainen T, Herzog W, Korhonen RK, Nieminen MT. Adiabatic rotating frame relaxation of MRI reveals early cartilage degeneration in a rabbit model of anterior cruciate ligament transection. Osteoarthritis Cartilage 2014;22:1444-52. [PubMed]
- Rautiainen J, Nissi MJ, Salo EN, Tiitu V, Finnilä MA, Aho OM, Saarakkala S, Lehenkari P, Ellermann J, Nieminen MT. Multiparametric MRI assessment of human articular cartilage degeneration: Correlation with quantitative histology and mechanical properties. Magn Reson Med 2014. [Epub ahead of print]. [PubMed]
- Takayama Y, Nishie A, Asayama Y, Ishigami K, Ushijima Y, Okamoto D, Fujita N, Morita K, Okuaki T, Honda H. T1ρ relaxation of the liver; Comparison of the continuous wave and stretched type adiabatic hyperbolic scant (HS) pulses for the assessment of liver function, Proc. Soc. Magn. Reson. Med., ISMRM Annual Meeting. Toronto, Canada, 2015:1535. Available online: http://indexsmart.mirasmart.com/ismrm2015/login.php
- Tannús A, Garwood M. Adiabatic pulses. NMR Biomed 1997;10:423-34. [PubMed]
- Andronesi OC, Bhat H, Reuter M, Mukherjee S, Caravan P, Rosen BR. Whole brain mapping of water pools and molecular dynamics with rotating frame MR relaxation using gradient modulated low-power adiabatic pulses. Neuroimage 2014;89:92-109. [PubMed]
- Borthakur A, Wheaton A, Charagundla SR, Shapiro EM, Regatte RR, Akella SV, Kneeland JB, Reddy R. Three-dimensional T1rho-weighted MRI at 1.5 Tesla. J Magn Reson Imaging 2003;17:730-6. [PubMed]
- Li X, Han ET, Ma CB, Link TM, Newitt DC, Majumdar S. In vivo 3T spiral imaging based multi-slice T(1rho) mapping of knee cartilage in osteoarthritis. Magn Reson Med 2005;54:929-36. [PubMed]
- Duvvuri U, Charagundla SR, Kudchodkar SB, Kaufman JH, Kneeland JB, Rizi R, Leigh JS, Reddy R. Human knee: in vivo T1(rho)-weighted MR imaging at 1.5 T--preliminary experience. Radiology 2001;220:822-6. [PubMed]
- Chen W, Takahashi A, Braun H, Gold G, Han E. 3D Quantitative Imaging of T1rho and T2. ISMRM 19th Annual Meeting. Montreal, Canada, 2011:231. Available online: http://cds.ismrm.org/protected/11MProceedings/files/231.pdf
- Witschey WR, Borthakur A, Elliott MA, Fenty M, Sochor MA, Wang C, Reddy R. T1rho-prepared balanced gradient echo for rapid 3D T1rho MRI. J Magn Reson Imaging 2008;28:744-54. [PubMed]
- Bonny JM, Zanca M, Boire JY, Veyre A. T2 maximum likelihood estimation from multiple spin-echo magnitude images. Magn Reson Med 1996;36:287-93. [PubMed]
- Raya JG, Dietrich O, Horng A, Weber J, Reiser MF, Glaser C. T2 measurement in articular cartilage: impact of the fitting method on accuracy and precision at low SNR. Magn Reson Med 2010;63:181-93. [PubMed]
- Hardy PA, Andersen AH. Calculating T2 in images from a phased array receiver. Magn Reson Med 2009;61:962-9. [PubMed]
- MacFall JR, Riederer SJ, Wang HZ. An analysis of noise propagation in computed T2, pseudodensity, and synthetic spin-echo images. Med Phys 1986;13:285-92. [PubMed]
- Mosher TJ, Dardzinski BJ. Cartilage MRI T2 relaxation time mapping: overview and applications. Semin Musculoskelet Radiol 2004;8:355-68. [PubMed]
- Miller AJ, Joseph PM. The use of power images to perform quantitative analysis on low SNR MR images. Magn Reson Imaging 1993;11:1051-6. [PubMed]
- Rice SO. Mathematical analysis of random noise. Bell System Tech J 1944;23:282-332.
- Bernstein MA, Thomasson DM, Perman WH. Improved detectability in low signal-to-noise ratio magnetic resonance images by means of a phase-corrected real reconstruction. Med Phys 1989;16:813-7. [PubMed]
- Gudbjartsson H, Patz S. The Rician distribution of noisy MRI data. Magn Reson Med 1995;34:910-4. [PubMed]
- Constantinides CD, Atalar E, McVeigh ER. Signal-to-noise measurements in magnitude images from NMR phased arrays. Magn Reson Med 1997;38:852-7. [PubMed]
- Mosher TJ, Smith H, Dardzinski BJ, Schmithorst VJ, Smith MB. MR imaging and T2 mapping of femoral cartilage: in vivo determination of the magic angle effect. AJR Am J Roentgenol 2001;177:665-9. [PubMed]
- Erickson SJ, Cox IH, Hyde JS, Carrera GF, Strandt JA, Estkowski LD. Effect of tendon orientation on MR imaging signal intensity: a manifestation of the "magic angle" phenomenon. Radiology 1991;181:389-92. [PubMed]
- Reiter DA, Lin PC, Fishbein KW, Spencer RG. Multicomponent T2 relaxation analysis in cartilage. Magn Reson Med 2009;61:803-9. [PubMed]
- Wang N, Xia Y. Dependencies of multi-component T2 and T1ρ relaxation on the anisotropy of collagen fibrils in bovine nasal cartilage. J Magn Reson 2011;212:124-32. [PubMed]
- Liu F, Chaudhary R, Hurley SA, Munoz Del Rio A, Alexander AL, Samsonov A, Block WF, Kijowski R. Rapid multicomponent T2 analysis of the articular cartilage of the human knee joint at 3.0T. J Magn Reson Imaging 2014;39:1191-7. [PubMed]


