
Parallel imaging with a combination of sensitivity encoding and generative adversarial networks
Introduction
Magnetic resonance imaging (MRI) is a widely used imaging modality with superior soft tissue contrast. However, a drawback of MRI is long acquisition time, which limits its clinical and research applications. Conventional Fourier transform based reconstructions (1) require line-by-line k-space sampling, which is the main restriction of the imaging speed.
Over the past 2 decades, many approaches have been proposed to accelerate MRI. Parallel imaging (PI) is one of the most common techniques, and has been widely used in clinical routine scans. With the introduction of multiple coils encoding, the required k-space data can be reduced so that the scan can be accelerated without causing artifacts in the reconstructed images. The most commonly used PI methods are sensitivity encoding (SENSE) (2) and generalized auto-calibrating partially parallel acquisitions (GRAPPA) (3). The aim of SENSE is to exploit the diversity of the spatial sensitivity of the receiver coils, and use it to recover the image from its aliased counterpart. It conglomerates under-sampled data from each independent coil with the modulation of weighting profiles from all coil sensitivity maps (4,5). On the other hand, GRAPPA seeks to build a kernel function from the auto-calibration signal (ACS) lines, and then use them to interpolate the missing k-space data. Recently, several other extensive approaches have also been introduced, including iterative self-consistent parallel imaging reconstruction (SPIRiT) (6), parallel imaging using eigenvector maps (ESPIRiT) (7), and annihilating filter based low-rank Hankel matrix (ALOHA) (8).
Although parallel imaging has made great progress in the last 2 decades, a persistent shortcoming is the significant degradation of signal-to-noise ratio (SNR) when high acceleration factors are applied (9). The image quality is often unacceptable for clinical application when the acceleration factor is >4 for 2-dimensional imaging. Taking SENSE as an example, the reconstruction performance depends on the accuracy of the estimated coil sensitivity maps (10). Noise in the estimated coil sensitivity maps will be amplified in the reconstructed images due to the ill-conditioned state of the inverse problem (9), which will cause severe aliasing artifacts (11). For some applications, sensitivity maps are often estimated from the ACS data, which contain some anatomical information, and cause certain residual artifacts in the reconstructed image. The noise amplification during SENSE reconstruction can be characterized by the geometry factor (g-factor) (2,12,13), which depends on the geometry of the receiver coil, acceleration factor, sampling pattern, and reconstruction algorithms.
Recently, many studies have utilized deep learning in image reconstruction due to its capability to extract high-level features from prior databases and preserve them in some abstract representations. For example, Wang et al. (14) incorporated the prior image generated by convolutional neural network (CNN) as an additional regularization term in the compressed sensing (CS) framework, and achieved superior performance compared to conventional CS methods. Hammernik et al. (15) employed a variational network (VN) to learn the image priors at multiple reconstruction stages and achieved good performance on knee imaging. Schlemper et al. (16) proposed a deep cascaded architecture by combining CNNs and data fidelity terms into an iterative framework for the reconstruction of under-sampled cardiac imaging. Ghodrati (17) showed that network training using the perceptual loss function achieved better agreement among radiologist scorings as compared to those networks using L1, L2, or structural similarity (SSIM) objective functions. Subhas (18) demonstrated the feasibility of accelerating knee MRI acquisition 6-fold through the application of a novel CNN architecture with deep layers.
More recently, generative adversarial networks (GAN) have also been exploited for MR image reconstructions. Generally speaking, GAN has 2 sub-networks, which are a generator and a discriminator. The generator is trained to learn the distribution of a certain dataset, while the discriminator is trained to distinguish between the generated samples and the real ones. Since the discriminator error is back-propagated to the generator, the errors of the discriminator and generator are conflicting, yielding an adversarial loss. Usage of the adversarial loss improves perceptual image quality compared to other loss functions. Several groups have utilized GAN for MR image reconstructions; GAN has the capability to generate data without explicitly modeling their probability density function (PDF). Mardani et al. (19) incorporated GAN into the conventional CS framework to remove the aliasing artifacts by projecting the image onto the low-dimensional manifold. Hammernik et al. (20) applied GAN to the VN model to reduce the blurring artifacts in the reconstructed sub-sampled image. Quan et al. (21) proposed a refined GAN architecture by applying cyclic data consistency loss into the forward reconstruction pipeline. The architecture consists of 2 residual networks concatenated in an end-to-end manner. Yang et al. (22) incorporated both image and frequency domain mean square errors (MSEs) into the objective function of GAN, and achieved better reconstruction performance than that of using image loss alone. Similarly, Zhang et al. (23) adopted both data consistency loss and perceptual loss into the adversarial objective function, and preserved more image details from limited k-space information.
The above-mentioned works have shown great potential for the application of deep learning in image reconstruction. However, it should be noted that most of the existing approaches treated MRI reconstruction as a single channel reconstruction problem. Our hypothesis is that the task of mapping from zero-filling (ZF) Fourier reconstructed images to full-sampled images is much more difficult than the task of removing g-factor artifacts from SENSE reconstructed images. When the acceleration factor is high, reconstructed images suffer from low SNR and severe g-factor artifacts if they are reconstructed by conventional PI/CS algorithms. Furthermore, a large number of under-sampled multi-coil data has been acquired in clinical routines. Our algorithm offers an option to improve those images in a retrospective manner without needing to perform an additional scan. Unlike other joint reconstruction methods, SENSE + GAN can be easily deployed in the post-processing workstations to improve image quality. Therefore, our method can correct previously gathered clinical data without affecting the clinical workflow, which is of great clinical importance.
In this study, we aimed to use GAN to remove g-factor artifacts from the SENSE reconstruction. Instead of using ZF images as the input for GAN, we applied standard SENSE reconstruction to the multi-coil under-sampled data and used them as the network input. A residual training framework was employed as the generator to remove the g-factor artifacts and reconstruct the final artifact-free images.
Methods
SENSE reconstruction
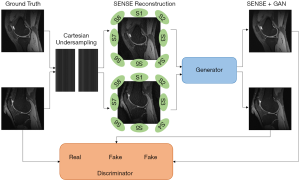
As shown in Figure 1, the input image of the GAN generator was reconstructed from under-sampling multi-coil k-space data by employing SENSE reconstruction. The SENSE reconstruction can be briefly described as follows:
[1]
Where IA represents the pixel values of the aliased image, I0 the un-aliased image, S the coil sensitivity map, and n represents the noise.
Suppose that the expectation of noise is zero, the covariance is ψ, then I0 can be calculated according to the following equation:
[2]
Where H represents the Hermite transpose operator.
Tikhonov regularization is adopted to solve the ill-conditioned linear equations of Eq. [1]:
[3]
Where λ2 represents the regularization factor (24),
The SENSE reconstruction was implemented by using a CG iterative algorithm with tolerance of 10-6 and maximum iterations of 30.
SENSE + GAN Architecture
Overview of SENSE + GAN
Here we name our method “SENSE + GAN”. The architecture of the proposed SENSE + GAN reconstruction method is shown in Figure 1. The multi-coil k-space data were reconstructed using SENSE (2) before feeding into GAN. The role of the generator was to remove the g-factor artifacts. The training process benefits more from the SENSE reconstruction compared to that from ZF reconstruction.
Generative adversarial framework
A standard GAN architecture was implemented in this study, which contains a generator (G) and a discriminator (D). The objective function is defined as follows:
[4]
The generator (G) maps the latent vectors drawn from some known prior pz (e.g., Gaussian distribution) to the sample space. The discriminator (D) tries to differentiate between the generated sample G(z) (fake) and the real data (real).
Instead of using random samples to initialize the training, here we use the idea of conditional GAN in which G is fed with SENSE/ZF reconstructed images x0. Conditional generated adversarial networks (CGAN) is an extension of the original GAN. Both the generator and the discriminator are added additional information as a condition, and it can be any information, such as label information, or other data, which can be seen as an improvement on CGAN that turns a standard unsupervised GAN into a supervised model. The adversarial loss Ladv is then defined as:
[5]
To facilitate the generator learning, we incorporate the pixel-wise image loss term into the final objective function:
[6]
In summary, the final objective function is defined as follows:
[7]
Where λ is a hyper-parameter to control the balance of loss between Ladv and Limg.
Model architecture
We adopted a residual U-Net architecture (Figure 2) as the generator, which consisted of an encoder, decoder, and symmetric skip connections between encoder and decoder blocks. The encoder was trained to compress the key information from the image artifacts to feature representations so that the decoder could regenerate the artifact-free image. The skip connections from encoder to decoder played a key role in reconstructing the fine details of the final image.
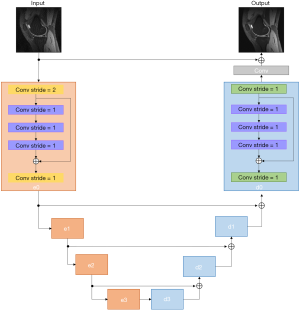
As shown in Figure 2, the encoder block (shaded in orange) accepted a 4D tensor input and performed 2D convolution with filter size of 3×3 along the imaging dimension. A stride of 2 was selected so that the network could perform down-sampling without an additional max-pooling layer. The number of feature maps is denoted in Figure 2. The decoder block (shaded in green) consists of 4 transposed convolution layers. It should be noted that we employed a residual block inside each encoder/decoder block. The purpose of using the residual block was to increase the depth of the generator G so that the g-factor artifacts could be better captured. The residual block consisted of 3convolution layers: (I) filter size of 3×3, stride of 1 for the first layer; (II) filter size of 3×3 for the second layer, and (III) filter size of 3×3, stride of 1 for the third layer. The residual blocks allowed us to effectively construct a deeper generator and discriminator without encountering problems of gradient vanishing and slow convergence (25).
Model training
Training and testing were performed using a programming wrapper, tensorpack (26), of the tensorflow (27) library, with graphics processing units (GPUs) of NVIDIA Tesla V100 (4 cores, each with 16 GB memory). We used the adaptive movement estimation (ADAM) algorithm for optimization, with a learning rate of 10−4 and epochs of 103. A mini-batch training strategy was applied with a batch size of 100. The total training time was approximately 8 h.
MRI dataset
We used a public knee database (28) containing 20 participants to evaluate our method. The images were obtained with a GE 3.0T scanner (GE Healthcare, Milwaukee, WI, USA) using a 3D fast spin-echo (FSE) CUBE sequence with proton density (PD) weighting [TE =25 ms, TR = 1,550 ms, field of view (FOV) = 160 mm, matrix size = 320×320×256]. All data were acquired with 8-channel knee coils (29). For each subject, 100 central slices were used for training and testing.
The data were retrospectively under-sampled in the k-space using Cartesian masks with sub-sampling rates of 50%, 25%, and 16.7%, which correspond to 2×, 4×, and 6× accelerations. Specifically, the kernel size was 5×5 and calibration region had 24 lines to estimate the sensitivity maps. The other part of k-space was uniformly sampled with different acceleration rates. To avoid overfitting, the network was trained with standard augmentations, including random rotation, shearing, and flipping. All the data were randomly split into 2 groups, i.e., 1,600 images for training and 400 images for validation.
Evaluation methods
We compared the performance of SENSE + GAN to ZF + GAN and VN with different acceleration factors (2×, 4×, 6×). For VN, the default parameters were selected according to their paper.
The ground truth images were calculated by performing square root of the sum-of-squares (SSOS) of the multi-coil full-sampled images.
To assess the quality of the reconstructed images, we applied 3 quality metrics to all the images, i.e., normalized root-mean-square error (NRMSE), peak signal-to-noise ratio (PSNR), and SSIM.
Results
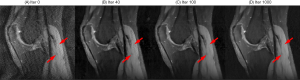
The proposed networks were trained with different acceleration factors (R = 2×, 4×, 6×). As shown in Figure 3, all the trainings converged within a few hundred iterations. The intermediate images during the training iterations are shown in Figure 4. The remaining g-factor artifacts in the SENSE reconstructed image were removed gradually during iterations.
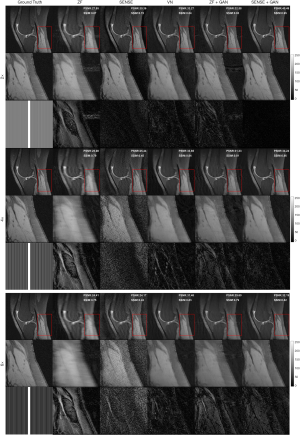
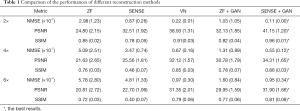
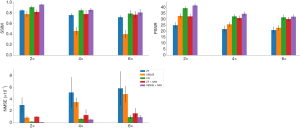
The representative images reconstructed from ZF, SENSE, VN, ZF + GAN, proposed SENSE + GAN, and ground truth data are shown in Figure 5. As illustrated in the zoomed-in images and the corresponding error maps, learning-based reconstruction methods showed better capability of removing aliasing artifacts compared to the SENSE algorithm. All methods except ZF achieved acceptable image quality when R=2. When 4-fold undersampling was applied, the images reconstructed by SENSE seemed to amplify the noise. In contrast, the error maps demonstrated that the deep learning-based approaches could effectively eliminate the noise amplification. In addition, there were obvious residual artifacts in the ZF + GAN images; the VN reconstructed image suffered from blurring artifacts in the blood vessel. However, the proposed SENSE + GAN method preserved those image details and textures more satisfactorily. At 6-fold acceleration, SENSE failed to reconstruct the image. The proposed SENSE + GAN had slightly better edge preservation and artifact suppression compared to VN and ZF + GAN, and this was further confirmed by quantitative analysis (Table 1). Specifically, SENSE + GAN yielded higher SSIM (SENSE + GAN: 0.81±0.06, ZF + GAN: 0.77±0.06, VN: 0.79±0.06) and lower NMSE (×10-7) (SENSE + GAN: 0.95±0.34, ZF + GAN: 1.60±0.84, VN: 0.97±0.30) with regular under-sampling.
Full table
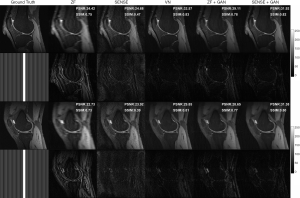
Two representative reconstruction examples with an acceleration factor of 6 are shown in Figure 6. It can be seen that the SENSE reconstruction is quite noisy at a high acceleration rate. But with the application of GAN, the noise level was largely reduced and the image quality is obviously improved. As illustrated in the error maps, the VN reconstructions have less undersampling artifacts and show better image quality than SENSE reconstructions. The ZF images are so blurry that even after applying GAN, some fine details in the images were lost, which is not acceptable for clinical applications. The performance of VN and the proposed SENSE + GAN were similar in terms of calculated PSNR (SENSE + GAN: 31.90±1.66, VN: 31.35±2.01) and SSIM (SENSE + GAN: 0.81±0.06, VN: 0.79±0.06).
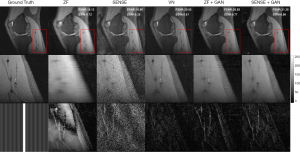
Zoomed-in comparison of different reconstruction methods with an acceleration factor of 6 is shown in Figure 7. Similarly, we can see that SENSE + GAN performed consistently better than other methods in terms of the overall pixel-wise errors and the preservations of fine details. Although the SENSE reconstructed image was much noisier than the ZF one, it preserved better image structures, which makes it easier for GAN to refine. The VN achieved a similar performance compared to SENSE + GAN in terms of image homogeneity and sharpness. These observations are supported by the quantitative analysis shown in Table 1.
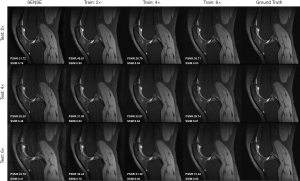
The results of applying our SENSE + GAN network trained with one acceleration factor to reconstruct images undersampled with other acceleration factors is shown in Figure 8. As we can see, the images reconstructed directly from the network trained on its corresponding acceleration factor achieved the best performance, which is consistent with the quantitative values. All 3 models (Train: 2×, 4×, 6×) achieved acceptable image quality when 2-fold undersampled images were tested. As for 4-fold undersampled images, applying the model trained on 2-fold and 4-fold undersampled images produced similar quality images. However, when adopting a 6-fold undersampled images trained model, the result yielded lower PSNR and SSIM. Compared to the 2-fold trained model, applying the 4-fold trained model to 6-fold undersampled data produced images with more realistic texture.
The reconstruction performances of different methods are reported in Table 1. It was observed that the proposed SENSE + GAN method performed the best among all the methods according to all measured quality metrics (highlighted with bold numbers in Table 1).
As shown in Figure 9, the deep learning-based reconstruction methods (VN, ZF + GAN, and SENSE + GAN) significantly outperformed SENSE reconstruction with acceleration factors of 2, 4, and 6 according to all metrics (P<0.01). Further, SENSE + GAN produced significantly better image quality than ZF + GAN (P<0.01). There were no significant differences between the metrics of SENSE + GAN and VN.
Discussion
This study has demonstrated the capability of using SENSE + GAN to produce faithful image reconstructions from highly undersampled k-space data. Our proposed method outperforms SENSE and ZF + GAN in terms of the measured quality metrics. The method performs especially well in preserving images details for an under-sampling factor of up to 6-fold.
The generator of GAN we adopted in this study was based on the residual U-net architecture. Once the g-factor artifact image is estimated, an artifact-free image can be obtained by subtracting the g-factor artifacts from the input image. The U-net (30) was initially proposed to solve image segmentation problems. The principle of residual learning (31) is to learn the difference between ground truth and input data. Previous studies (32,33) have shown that residual U-net can effectively remove reconstruction artifacts while preserving image structures in CT images. Residual learning is also capable of alleviating the vanishing gradient problem (33). The advantage of residual U-net is originated from its enlarged receptive fields that can easily capture globally distributed artifact patterns and make the network converge efficiently (34).
Multi-channel imaging is now widely used in clinical routines as multi-channel data can provide richer imaging information. However, most deep learning based reconstruction approaches are limited by the usage of single-coil images. To address this issue, several multi-channel based reconstruction algorithms have been proposed. Moreover, most multi-channel reconstruction networks use synthetic single-coil images, such as a synthesized coil-combined image or coil-combined retrospectively undersampled k-space data. For example, the VN (15) approach was presented to learn an end-to-end reconstruction procedure for multi-channel MR data. Then, the PI-CNN network (35), which integrated multi-channel undersampled k-space data and exploited them through parallel imaging was proposed. Furthermore, the Deepcomplex CNN (36) was introduced to get the de-aliased multi-channel images without the need for any prior information. Moreover, a reconstruction framework named Sampling-Augmented Neural neTwork with Incoherent Structure (SANTIS) (37) was proposed to improve the robustness of a trained network against the discrepancy of undersampling schemes. The large amount of information contained in the prospective under-sampled k-space data is missing from these coil-combined under-sampled data. However, our proposed framework was the first to perform a SENSE reconstruction of the multi-channel data and then feed the SENSE image into the GAN network to remove the g-factor artifacts. Thus, the proposed SENSE + GAN framework can be effectively applied to the prospectively undersampled data in practical clinical applications. Nevertheless, it is not applicable to reconstruct images with the single-coil-based network. From this perspective, our approach is closer to its real applications. Moreover, unlike most other deep learning-based reconstruction algorithms, SENSE + GAN has the advantage of separating the reconstruction into 2 steps. The PI reconstructed images, which are treated as intermediate results in our algorithm, are valuable for routine clinical use. In that sense, we can generate PI reconstruction images as well as GAN reconstruction results, which means that we can provide better images based on conventional methods without affecting the entire clinical workflow. Thus, the proposed SENSE + GAN can be performed in a retrospective manner in most hospitals.
The results show that if the number of the acceleration factor is drastically different between the training and test stages, the proposed framework requires other training processes to achieve the best performance. Dar et al. (38) have proposed a transfer-learning approach to handle the problem of data scarcity in network training for accelerated MRI. Its applicability to our framework will be explored in future work.
In addition to residual U-net based GAN, the architecture of GAN can also be extended to enhance the reconstruction performance further. For example, the RefineGAN (21) model has been demonstrated to perform better than single GAN. It is worth noting that although we demonstrated our method on Cartesian under-sampling, it is also feasible to transfer it to different under-sampling patterns such as radial and spiral trajectories. Since the artifacts have different patterns in these trajectories, further validation studies should be performed to assess the flexibility of our method. In addition, various approaches (14,22,39-44) combining deep learning and CS have been studied in recent years to maximize the acceleration of MRI acquisition. The reference images generated by the network were then fed into a forward model to obtain the final reconstruction results. Our future plan is to incorporate CS into our framework to further improve the reconstruction with higher acceleration factors.
Our study has several limitations. First, there is a requirement to obtain fully sampled datasets before training. However, fully sampled data may not be available in several applications due to motion, which discourages the use of fully sampled training labels for those datasets. Therefore, it is necessary to apply some unsupervised training strategies in those applications. Second, current analysis only considers training the networks using the square root of sum-of-squares images. We hope to investigate multi-channel data training in the future, as we believe that the additional richness of multi-channel CNN has the potential to further improve the reconstruction performance. Our method can also be extended to 3D imaging. Third, we should enlarge the dataset to include both healthy participants and patients.
Conclusions
We have presented a novel framework for accelerated MRI reconstruction by combining SENSE reconstruction with GAN. Results show that the proposed method is capable of producing faithful image reconstructions from highly under-sampled k-space data. The SENSE + GAN method consistently outperforms the SENSE and ZF + GAN approaches in terms of all measured quality metrics. The improvement of reconstruction is more obvious for higher under-sampling rates, which is promising for many clinical applications.
Acknowledgments
Funding: This study was funded by the National Natural Science Foundation of China (61902338), and in part by the National Natural Science Foundation of China (No. 62001120) and the Shanghai Sailing Program (No. 20YF1402400).
Footnote
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at http://dx.doi.org/10.21037/qims-20-518). JL reports grants from National Natural Science Foundation of China (No. 61902338), during the conduct of the study; Chengyan Wang reports grants from Shanghai Sailing Program (No. 20YF1402400), grants from National Natural Science Foundation of China (No. 62001120), during the conduct of the study.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Lustig M, Donoho DL, Santos JM, Pauly JM. Compressed Sensing MRI. IEEE Signal Process Mag 2008;25:72-82. [Crossref]
- Pruessmann KP, Weiger M, Scheidegger MB, Boesiger P. SENSE: sensitivity encoding for fast MRI. Magn Reson Med 1999;42:952-62. [Crossref] [PubMed]
- Griswold MA, Jakob PM, Heidemann RM, Nittka M, Jellus V, Wang J, Kiefer B, Haase A. Generalized autocalibrating partially parallel acquisitions (GRAPPA). Magn Reson Med 2002;47:1202-10. [Crossref] [PubMed]
- Hoge WS, Brooks DH, Madore B, Kyriakos WE. A tour of accelerated parallel MR imaging from a linear systems perspective. Concepts Magn Reson Part A 2010;27A:17-37. [Crossref]
- Zhang J, Chu Y, Ding W, Kang L, Xia L, Jaiswal S, Wang Z, Chen Z. HF-SENSE: an improved partially parallel imaging using a high-pass filter. BMC Med Imaging 2019;19:27. [Crossref] [PubMed]
- Lustig M, Pauly JM. SPIRiT: Iterative self-consistent parallel imaging reconstruction from arbitrary k-pace. Magn Reson Med 2010;64:457-71. [Crossref] [PubMed]
- Uecker M, Lai P, Murphy MJ, Virtue P, Elad M, Pauly JM, Vasanawala SS, Lustig M. ESPIRiT-an eigenvalue approach to autocalibrating parallel MRI: where SENSE meets GRAPPA. Magn Reson Med 2014;71:990-1001. [Crossref] [PubMed]
- Lee J, Jin KH, Ye JC. Reference-free single-pass EPI Nyquist ghost correction using annihilating filter-based low rank Hankel matrix (ALOHA). Magn Reson Med 2016;76:1775-89. [Crossref] [PubMed]
- Hamilton J, Franson D, Seiberlich N. Recent Advances in Parallel Imaging for MRI. Progress in Nuclear Magnetic Resonance Spectroscopy 2017;101:71-95. [Crossref] [PubMed]
- Hoge WS, Brooks DH. Using GRAPPA to improve autocalibrated coil sensitivity estimation for the SENSE family of parallel imaging reconstruction algorithms. Magn Reson Med 2008;60:462-7. [Crossref] [PubMed]
- Zhang J, Chu Y, Ding W, Kang L, Xia L, Jaiswal S, Wang Z, Chen Z. HF-SENSE: an improved partially parallel imaging using a high-pass filter. BMC Med Imaging 2019;19:27. [Crossref] [PubMed]
- Breuer FA, Kannengiesser SM. General formulation for quantitative G-factor calculation in GRAPPA reconstructions. Magn Reson Med 2009;62:739-46. [Crossref] [PubMed]
- Robson PM, Grant AK, Madhuranthakam AJ, Lattanzi R, Sodickson DK, Mckenzie CA. Comprehensive quantification of signal-to-noise ratio and g-factor for image-based and k-space-based parallel imaging reconstructions. Magn Reson Med 2008;60:895-907. [Crossref] [PubMed]
- Wang S, Su Z, Ying L, Peng X, Zhu S, Liang F, Feng D, Liang D. Accelerating magnetic resonance imaging via deep learning. Proc IEEE Int Symp Biomed Imaging 2016;2016:514-7. [PubMed]
- Hammernik K, Klatzer T, Kobler E, Recht MP, Sodickson DK, Pock T, Knoll F. Learning a variational network for reconstruction of accelerated MRI data. Magn Reson Med 2018;79:3055-71. [Crossref] [PubMed]
- Schlemper J, Caballero J, Hajnal JV, Price AN, Rueckert D. A deep cascade of convolutional neural networks for dynamic MR image reconstruction. IEEE Trans Med Imaging 2018;37:491-503. [Crossref] [PubMed]
- Ghodrati V, Shao J, Bydder M, Zhou Z, Hu P. MR image reconstruction using deep learning: evaluation of network structure and loss functions. Quant Imaging Med Surg 2019;9:1516-27. [Crossref] [PubMed]
- Subhas N, Li H, Yang M, Winalski CS, Polster J, Obuchowski N, Mamoto K, Liu R, Zhang C, Huang P, Gaire SK, Liang D, Shen B, Li X, Ying L. Diagnostic interchangeability of deep convolutional neural networks reconstructed knee MR images: preliminary experience. Quant Imaging Med Surg 2020;10:1748-62. [Crossref] [PubMed]
- Mardani M, Gong E, Cheng JY, Vasanawala SS, Zaharchuk G, Lei X, Pauly JM. Deep Generative Adversarial Neural Networks for Compressive Sensing MRI. IEEE Trans Med Imaging 2019;38:167-79. [Crossref] [PubMed]
- Hammernik K, Kobler E, Pock T, Recht MP, Sodickson DK, Knoll F. editors. Variational Adversarial Networks for Accelerated MR Image Reconstruction. Joint Annual Meeting ISMRM-ESMRMB 2018.
- Quan TM, Nguyen-Duc T, Jeong WK. Compressed sensing MRI reconstruction using a generative adversarial network with a cyclic loss. IEEE Trans Med Imaging 2018;37:1488-97. [Crossref] [PubMed]
- Yang G, Yu S, Dong H, Slabaugh G, Dragotti PL, Ye X, Liu F, Arridge S, Keegan J, Guo Y. DAGAN: Deep De-Aliasing Generative Adversarial Networks for Fast Compressed Sensing MRI Reconstruction. IEEE Trans Med Imaging 2018;37:1310-21. [Crossref] [PubMed]
- Zhang P, Wang F, Xu W, Li Y, editors. Multi-channel generative adversarial network for parallel magnetic resonance image reconstruction in k-space. International Conference on Medical Image Computing and Computer-Assisted Intervention; Springer, 2018.
- Lin FH, Kwong KK, Belliveau JW, Wald LL. Parallel imaging reconstruction using automatic regularization. Magn Reson Med 2004;51:559-67. [Crossref] [PubMed]
- He K, Zhang X, Ren S, Jian S. Deep Residual Learning for Image Recognition. IEEE Conference on Computer Vision & Pattern Recognition; 2016.
- Tensorpack Documentation. Available online: http://tensorpack.readthedocs.io/
- Tensorflow. Available online: http://www.tensorflow.org/
- Zech CJ, Herrmann KA, Huber A, Dietrich O, Stemmer A, Herzog P, Reiser MF, Schoenberg SO. High‐resolution MR‐imaging of the liver with T2‐weighted sequences using integrated parallel imaging: comparison of prospective motion correction and respiratory triggering. J Magn Reson Imaging 2004;20:443-50. [Crossref] [PubMed]
- Epperson K, Sawyer AM, Lustig M, Alley M, Uecker M, Virtue P, Lai P, Vasanawala S, editors. Creation of fully sampled MR data repository for compressed sensing of the knee. 2013 Meeting Proceedings. Section for Magnetic Resonance Technologists; 2013.
- Ronneberger O, Fischer P, Brox T, editors. U-net: Convolutional networks for biomedical image segmentation. International Conference on Medical image computing and computer-assisted intervention; Springer: 2015.
- Kim J, Kwon Lee J, Mu Lee K. Accurate image super-resolution using very deep convolutional networks. Proceedings of the IEEE conference on computer vision and pattern recognition; 2016.
- Lee H, Lee J, Kim H, Cho B, Cho S. Deep-Neural-Network-Based Sinogram Synthesis for Sparse-View CT Image Reconstruction. IEEE Trans Radiat Plasma Med Sci 2018;3:109-19. [Crossref]
- Jin KH, McCann MT, Froustey E, Unser M. Deep convolutional neural network for inverse problems in imaging. IEEE Trans Image Process 2017;26:4509-22. [Crossref] [PubMed]
- Han YS, Yoo J, Ye JC. Deep residual learning for compressed sensing CT reconstruction via persistent homology analysis. arXiv preprint arXiv:06391 2016.
- Zhou Z, Han F, Ghodrati V, Gao Y, Yin W, Yang Y, Hu P. Parallel imaging and convolutional neural network combined fast MR image reconstruction: Applications in low‐latency accelerated real‐time imaging. Medical physics 2019;46:3399-413. [Crossref] [PubMed]
- Wang S, Cheng H, Ying L, Xiao T, Ke Z, Zheng H, Liang D. DeepcomplexMRI: Exploiting deep residual network for fast parallel MR imaging with complex convolution. Magnetic Resonance Imaging 2020;68:136-47. [Crossref] [PubMed]
- Liu F, Samsonov A, Chen L, Kijowski R, Feng L. SANTIS: sampling‐augmented neural network with incoherent structure for MR image reconstruction. Magn Reson Med 2019;82:1890-904. [Crossref] [PubMed]
- Dar SUH, Özbey M, Çatlı AB, Çukur T. A Transfer-Learning Approach for Accelerated MRI using Deep Neural Networks. Magn Reson Med 2020;84:663-85. [Crossref] [PubMed]
- Quan TM, Jeong WK. editors. Compressed sensing reconstruction of dynamic contrast enhanced MRI using GPU-accelerated convolutional sparse coding. 2016 IEEE 13th International Symposium on Biomedical Imaging (ISBI); IEEE: 2016.
- Lee D, Yoo J, Ye JC. Deep residual learning for compressed sensing MRI. 2017 IEEE 14th International Symposium on Biomedical Imaging (ISBI 2017); IEEE: 2017.
- Sun J, Li H, Xu Z, editors. Deep ADMM-Net for compressive sensing MRI. Advances in neural information processing systems; 2016.
- Lee D, Yoo J, Ye JC. Deep artifact learning for compressed sensing and parallel MRI. arXiv preprint, arXiv: 01120 2017.
- Mardani M, Gong E, Cheng JY, Vasanawala S, Zaharchuk G, Alley M, Thakur N, Han S, Dally W, Pauly JM. Deep generative adversarial networks for compressed sensing automates MRI. arXiv: 170600051 2017.
- Yu S, Dong H, Yang G, Slabaugh G, Dragotti PL, Ye X, Liu F, Arridge S, Keegan J, Firmin D. Deep de-aliasing for fast compressive sensing MRI. arXiv preprint arXiv: 07137 2017.



