Three-dimensional fast single-point macromolecular proton fraction mapping of the human brain at 0.5 Tesla
Introduction
The magnetization transfer (MT) effect caused by cross-relaxation between the protons of water and macromolecules is widely used in MRI to modify tissue contrast and quantify tissue properties. Theoretical description of the MT effect is based on the classical two-pool model (1), which can be translated into quantitative imaging techniques producing parametric maps of the macromolecular proton fraction (MPF), cross-relaxation rate constant, and relaxation times of water and macromolecular protons (2-6). MPF maps have been shown to be of particular interest for measuring subtle brain pathological changes related to microscopic demyelination and undetectable by other MRI methods in both clinical (7,8) and preclinical (9-11) settings. MPF also demonstrated high sensitivity to the earliest stages of myelin development in the fetal (12-14) and pediatric (14,15) brain.
Quantitative imaging of the MT effect is based on an analysis of a series of source MT-weighted images obtained with variable offset frequency and power of an off-resonance radiofrequency (RF) saturation pulse (2-5). While the conventional analysis of quantitative MT data requires at least four MT-weighted images (4), the recent single-point method (5,6) provides accurate MPF maps from one such image. This method allows MPF measurements based on the iterative solution of the pulsed steady-state MT matrix equation (3-5) while constraining other model parameters. Specifically, the values of the cross-relaxation rate constant, T2 of macromolecular protons, and the ratio T2/T1 for free water protons are assumed constant across brain tissues due to their small tissue-dependent variability, whereas T1 is measured independently (5). The best accuracy of the method is achieved if an MT-weighted image is acquired at optimal saturation conditions (offset frequency and saturation power), which minimize sensitivity of the model to possible variations in the constrained parameters (5). In the latest synthetic-reference modification of the single-point method (6), an MPF map is reconstructed in a two-step algorithm, where a T1 map and a synthetic-reference image are computed from T1- and proton density (PD)-weighted spoiled gradient-echo images at the first step, and the MPF map is obtained at the second step from the pulsed MT model fit with the MT-weighted spoiled gradient-echo image, T1 map, and synthetic reference image as input data. As such, this technique allows reconstructing an MPF map from the three source images with T1, PD, and MT contrast weightings, thus enabling the fastest possible data acquisition procedure.
Low-field MRI equipment offers cost-effective access to this diagnostic modality in developing countries and rural clinical settings (16). In developed countries, the use of low-field magnets remains the main option in certain specialized systems, such as open, intraoperative, and portable scanners (16). Quantitative imaging is usually disadvantaged in low magnetic fields due to signal-to-noise ratio (SNR) limitations (16). So far, fast MPF mapping has been implemented only at high magnetic fields (1.5 T and above). Introduction of this method into low-field MRI could substantially enhance the potential of the existing equipment in applications to demyelinating diseases and brain development. This proof-of-concept study aimed to evaluate the feasibility of single-point MPF mapping of the human brain at 0.5 T and assess the accuracy of a low-field implementation of the method by comparing the results with validated high-field (3 T) MPF measurements from the literature.
Materials and methods
Theory and Simulations
Simulations were performed to optimize MT saturation conditions for low-field MPF mapping. We define the MPF-to-noise-ratio (MNR) as the ratio of a fitted MPF value to its variance due to noise propagated from the source images: MNR=MPF/σMPF. To estimate σMPF, we adapted Eq. [11] from Ref. (5):
where mz=SMT/Sref is the normalized longitudinal magnetization of the free water pool generated by the spoiled gradient-echo sequence with off-resonance saturation, which is equal to the ratio of signals obtained with (SMT) and without (Sref) saturation and computed using the two-pool pulsed steady-state matrix model (3-5) for a set of model parameters (MPF, T1, cross-relaxation rate constant R, and T2 of free water (T2F) and bound macromolecular (T2B) protons); and SNRref is SNR of the reference image with the signal intensity Sref. Note that the reference image can be either acquired with sequence parameters similar to those used for the MT-weighted image as specified in the initial single-point method design (5) or computed from the PD and T1 maps according to the synthetic reference algorithm (6). Simulated dependences of MNR on the offset frequency (Δ) and flip angle of the saturation pulse (FAMT) were examined for the sets of model parameters corresponding to white matter (WM) with MPF =13.5%, T1=0.4 s, R =20 s−1, T2F =0.04 s, and T2B =10−5 s and grey matter (GM) with MPF =6.5%, T1=0.6 s, R =20 s−1, T2F =0.06 s, and T2B =10−5 s. The above estimates of MPF, R, and T2B were taken from high-field measurements (5,17) due to their independence of magnetic field (17). T2F values were set according to 1.5 T data (2), since field dependence of this parameter is relatively weak (17). T1 values at 0.5 T were adopted from (3). T1 of the water and macromolecular proton pools were assumed equal to the observed T1 (3,5). An additional series of simulations was performed to demonstrate the effect of magnetic field strength (0.5, 1.5, and 3 T) on MNR for WM. In these simulations, SNRref and T1 were assumed to depend on magnetic field [T1 =650 ms for 1.5 T (2) and 1,000 ms for 3T (5)], and T2F =22 ms was used for 3 T (5). Pulse sequence parameters corresponded to the experimental protocol outlined below. Simulations were performed using custom-written C-language software.
Experiments
The study involved three healthy volunteers (two females, one male; age 21, 22, and 60 years). The study protocol was approved by the local ethical committee and conformed to the provisions of the Helsinki Declaration. Written informed consent was obtained from all participants.
A 0.5 T whole-body scanner Tomikon S50 (Bruker Medizintechnik GmbH, Ettlingen, Germany) was used for data acquisition. It is equipped with a superconducting magnet with a bore diameter of 60 cm and a gradient system with 17 mT/m maximal strength. RF field was generated by a 60-cm-diameter whole-body transmit coil. MRI signal was detected by a quadrature receive-only head coil. Whole-brain scans were obtained in a sagittal projection with the voxel size of 1.5×1.5×2 mm3 (FOV =24×24×17.6 cm3, matrix size 160×160×88). To acquire source images, 3D spoiled gradient-echo sequences were used with TR/TE =25/5 ms for PD- and T1-weighted scans and TR/TE =30/5 ms for an MT-weighted scan. Excitation flip angles were 5, 30, and 10° for PD-, T1-, and MT-weighted images, respectively, with a 1 ms rectangular non-selective RF pulse being used. The MT-pulse had a Gaussian shape, duration of 8 ms, FAMT =736° (limited by the maximal achievable B1 amplitude of 6 µT), and Δ =1.5 kHz, which provide nearly optimal MPF sampling conditions for 0.5 T according to simulation results detailed below. The total scan time was 19 minutes.
Reconstruction of MPF maps was carried out using custom-written C-language software according to the single-point synthetic-reference algorithm (5,6). SNR was calculated for the synthetic-reference image in the frontal WM regions-of-interest (ROI). Since noise is thresholded prior to computation of parametric maps, we measured the signal intensity in the reconstructed reference image (Sref), whereas the standard deviation of noise (SDn) was taken as an average value from the background of source images. SNR was calculated according to the formula: SNR=0.65Sref/SDn (18). MPF values for different WM and GM structures were measured in circular ROI using ImageJ software (19). The measurements were performed in the same structures as those in the earlier study at 3 T (5). Prior to the measurements, the MPF data matrix was interpolated to the isotropic voxel size of 1×1×1 mm3.
Mean MPF values from the participants were compared to the literature data (5) across all anatomic structures using the two-tailed t-test for independent samples. Pearson’s correlation coefficient (r) between the reported in the literature (5) and obtained in this study MPF measurements was assessed for structure-averaged data.
Results
Simulated dependences of MNR on the offset frequency and flip angle of the saturation pulse for WM and GM computed with the sequence parameters used in the imaging protocol are presented in Figure 1. Simulations suggest that MNR is maximized at Δ≈1.5–2 kHz (Figure 1A) and FAMT ≈1,000°–1,200°. Figure 2 demonstrates the effect of magnetic field strength on MNR and optimal saturation conditions. MNR substantially increases in higher fields due to the available gain in SNR of source images. An optimal offset frequency increases (Figure 2A) and an optimal saturation flip angle decreases (Figure 2B) with an increase in field strength. Specifically, for FAMT =700°, optimal Δ shifts towards 3 kHz for 1.5 T and 4 kHz for 3 T (Figure 2A). Optimal FAMT at Δ =1.5 kHz is achieved in the vicinity of 700° at 1.5 T and 500° at 3 T (Figure 2B).
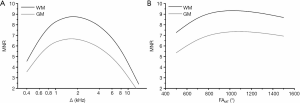
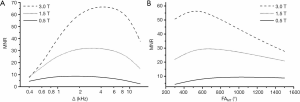
Figure 3 shows a scheme for obtaining an MPF map in accordance with the single-point synthetic-reference algorithm. The source PD-, T1- and MT-weighted MR images are shown in Figure 3A,B,C. The first two images were used to calculate the reference image (Figure 3D) and T1 map (Figure 3E). The images in Figure 3C,D,E were used to calculate the MPF map (Figure 3F). SNR of the synthetic-reference image in frontal WM was 32.5±4.2.
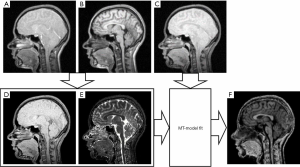
Figure 4 illustrates the visual appearance of brain anatomic structures on a 3D MPF map obtained at 0.5 T. The reformatted views of the MPF map show sharp contrast between WM and GM. For certain brain structures, MPF maps enable image contrast features unavailable for conventional imaging methods in low-field settings. For example, the cross-section of the MPF map at the pons level (Figure 4F) demonstrates hyperintensity of the two pairs of fiber bundles corresponding to the corticospinal tract (anterior pair) and the proximally located medial lemniscus and central tegmental tract (posterior pair) due to fine distinctions in myelination between these compact tracts and the rest of pontine WM. The observed pattern appears in close agreement with the human brainstem anatomy on myelin-stained histological sections according to the literature (20). Also, the GM structures with high iron content (globus pallidus, substantia nigra, and dentate nucleus), which lack GM contrast features on conventional T1- and T2-weighted images, demonstrate characteristic hypointensity in MPF maps, similar to the rest of GM (Figure 4E,G,H).
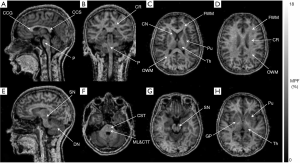
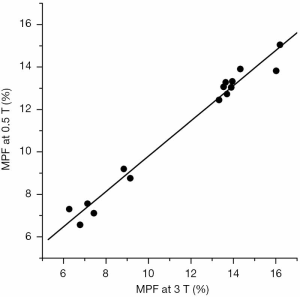
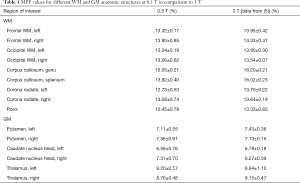
MPF values for different WM and GM anatomic structures at 0.5 T are summarized in Table 1 along with 3 T data published earlier (5). No significant difference across anatomic structures was found between MPF measurements obtained at 0.5 and 3 T magnetic field strengths (P=0.7). Structure-averaged MPF values measured at 0.5 and 3 T were strongly correlated (r=0.988, P<0.001; Figure 5).
Full table
Discussion
We present the first implementation of the fast MPF mapping method in low-field MRI. At magnetic field of 0.5 T, anatomically consistent 3D MPF maps were obtained with high spatial resolution and an acceptable scan time. Excellent quantitative agreement between MPF measurements at 0.5 and 3 T confirms the insensitivity of this parameter to magnetic field strength. A similar conclusion was reported earlier based on small animal brain imaging in high (3 T) and ultra-high (11.7 T) magnetic fields (17,21). Our results therefore extend the range of field strengths, where MPF can be reliably used as a quantitative measure of brain myelination. In contrast to the relaxation times T1 and T2 and myelin measures derived from multicomponent relaxation analysis (22-24), MPF provides nearly identical quantitative values for human and animal brain tissues and can be easily measured at a wide range of magnetic field strengths. Taken together with the previous studies (5-15,17,25,26), this report validates the use of MPF as a uniform myelin biomarker in magnetic fields spanning from 0.5 to 14 T.
Implementation of fast MPF mapping in low magnetic fields poses several technical challenges. One is related to a generally low SNR, which approximately scales proportionally to B03/2 (16). In the initially published optimal design (5), high SNR in source images (>100) has been recommended to enable accurate MPF measurements. However, with the advent of ultrafast applications at 1.5 T (12-14), it was demonstrated that SNR requirements in single-point MPF mapping can be substantially relaxed (12). Particularly, the recent study (12) showed that MPF estimates are minimally affected by the noise bias for SNR as low as 15–20, and the method still provides accurate measurements in tissues despite increased noise variance. In the presented 0.5 T protocol, the calculated SNR in reference images was about 30, for which the effect of noise bias is practically negligible. Another problem is associated with T1 shortening, which adversely affects saturation of macromolecular protons. Magnetization dynamics in the two-pool model under pulsed off-resonance saturation (3) involves several concurrent processes including saturation of the macromolecular pool by radiofrequency field, dissipation of magnetic energy from both macromolecular and water pools to the lattice via T1 mechanism, and cross-relaxation between the pools. Additionally, direct saturation of water protons may occur at relatively low offset frequencies and/or high saturation power. Complex interplay between these processes affect the sensitivity of the MT-weighted signal to MPF and propagation of noise into the resulting maps. The results of numerical optimization presented in this and earlier (5) studies suggest that optimal saturation conditions can be found to maximize precision of MPF measurements, and that such conditions are field-dependent. As the rate of spin-lattice relaxation increases due to T1 shortening in low magnetic fields, saturation becomes less efficient, and signal intensity changes become less sensitive to cross-relaxation (3,5). To alleviate this effect, offset frequency of the saturation pulse needs to be reduced from the optimal range of Δ =4–7 kHz suggested for 3 T imaging (5) to 1.5–2 kHz, which results in an increase in the saturation rate (3,5). For the same reason, an increase of the saturation flip angle appears beneficial for low-field MPF mapping, though this parameter may be restricted by hardware capabilities and specific absorption rate limitations. Accurate brain MPF values obtained in this study suggest that a reasonable decrease of saturation offset frequency can be safely used in low-field MPF mapping applications. However, care must be taken regarding further shifting Δ towards water resonance, since it may lead to excessive direct saturation of the free water pool (5). Accordingly, additional offset frequency reduction in low-field MPF mapping may require longer radiofrequency pulses to narrow effective saturation bandwidth.
Low-field MPF mapping also offers certain technical advantages over high-field implementations. First, the above mentioned reduction of saturation offset frequency allows using unmodified clinical MT sequences for the fast MPF mapping method. Most manufacturers have implemented MT-weighted sequences with fixed Δ in a range of 1–2 kHz (12), which appears optimal for low-field MPF measurements. Second, non-uniformity of B1 field was shown to be a critical source of errors in MPF mapping at 3 T (27), where specialized B1 mapping sequences are needed to correct MPF maps. In low fields, B1 field inhomogeneity is very minor (16,27) and B1 correction can be safely omitted.
This study has certain technical limitations. First, a particular shortcoming of the presented imaging protocol is a long scan time, which was caused by not only a field-related SNR drop but also some limitations of our hardware. Specifically, a simple quadrature reception coil resulted in a rather low SNR and impossibility to employ parallel imaging for scan acceleration. Additionally, a relatively weak gradient system of our scanner required a fairly long TR =25 ms for PD and T1-weighted images, which could be reduced without any loss of the method performance. We expect that modern low-field MRI systems equipped with multi-channel coils and parallel imaging capabilities would enable 1.5–2-fold scan time reduction while maintaining similar spatial resolution. Another strategy to mitigate the long scan time problem in clinical settings could be an increase of the slice thickness to 5–6 mm, which would match that typically used in routine low-field clinical protocols. Second, this study did not employ recent improved techniques for MPF and T1 mapping, which could be beneficial for the accuracy and precision of MPF estimation. Newer MPF mapping algorithms enable corrections of errors caused by bi-exponential longitudinal relaxation (28) and non-exchangeable free water content (29) in tissues. The single-point MPF mapping method may also benefit from the controlled saturation T1 mapping approach (30) offering improved reproducibility and inherent correction of errors caused by the MT effect. While the above techniques (28-30) were not tested in this pilot study, their translation into low-field MPF mapping seems rather straightforward.
In conclusion, this study provides a compelling evidence of the independence of MPF of magnetic field, since quantitative MPF estimates obtained using a low-field scanner (0.5 T) appeared very close to those reported for high-field systems (3 T and above). The presented results confirm the utility of MPF as an absolute scale for MRI-based myelin content measurements across a wide range of magnetic field strengths. From the practical standpoint, our results demonstrate the feasibility of fast MPF mapping with low-field MRI equipment that extends the applicability of the method to rural clinical settings with cheapest available MRI hardware.
Acknowledgments
Funding: The study was supported by the Ministry of Education and Science of the Russian Federation within the State Assignment Project No. 18.2583.2017/4.6. Experiments were carried out at the “Biospectrotomography” Shared Instrumentation Center (Lomonosov Moscow State University) under support of the Russian Foundation for Basic Research grant No.19-29-10015. Numerical simulations and data analysis were supported by the Russian Science Foundation Project No.19-75-20142. Software for MPF map reconstruction was distributed under support of the United States National Institutes of Health High-Impact Neuroscience Research Resource grant R24NS104098.
Footnote
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at http://dx.doi.org/10.21037/qims-19-1057). The authors have no conflicts of interest to declare.
Ethical Statement: The study protocol was approved by the local ethical committee and conformed to the provisions of the Helsinki Declaration. Written informed consent was obtained from all participants.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Henkelman RM, Huang X, Xiang QS, Stanisz GJ, Swanson SD, Bronskill MJ. Quantitative interpretation of magnetization transfer. Magn Reson Med 1993;29:759-66. [Crossref] [PubMed]
- Sled JG, Pike GB. Quantitative imaging of magnetization transfer exchange and relaxation properties in vivo using MRI. Magn Reson Med 2001;46:923-31. [Crossref] [PubMed]
- Yarnykh VL. Pulsed Z-spectroscopic imaging of cross-relaxation parameters in tissues for human MRI: theory and clinical applications. Magn Reson Med 2002;47:929-39. [Crossref] [PubMed]
- Yarnykh VL, Yuan C. Cross-relaxation imaging reveals detailed anatomy of white matter fiber tracts in the human brain. Neuroimage 2004;23:409-24. [Crossref] [PubMed]
- Yarnykh VL. Fast macromolecular proton fraction mapping from a single off-resonance magnetization transfer measurement. Magn Reson Med 2012;68:166-78. [Crossref] [PubMed]
- Yarnykh VL. Time-efficient, high-resolution, whole brain three-dimensional macromolecular proton fraction mapping. Magn Reson Med 2016;75:2100-6. [Crossref] [PubMed]
- Yarnykh VL, Bowen JD, Samsonov A, Repovic P, Mayadev A, Qian P, Gangadharan B, Keogh BP, Maravilla KR, Henson LK. Fast Whole-Brain Three-dimensional Macromolecular Proton Fraction Mapping in Multiple Sclerosis. Radiology 2015;274:210-20. [Crossref] [PubMed]
- Yarnykh VL, Krutenkova EP, Aitmagambetova G, Repovic P, Mayadev A, Qian P, Jung Henson LK, Gangadharan B, Bowen JD. Iron-Insensitive Quantitative Assessment of Subcortical Gray Matter Demyelination in Multiple Sclerosis Using the Macromolecular Proton Fraction. Am J Neuroradiol 2018;39:618-25. [Crossref] [PubMed]
- Khodanovich MY, Kisel AA, Akulov AE, Atochin DN, Kudabaeva MS, Glazacheva VY, Svetlik MV, Medvednikova YA, Mustafina LR, Yarnykh VL. Quantitative assessment of demyelination in ischemic stroke in vivo using macromolecular proton fraction mapping. J Cereb Blood Flow Metab 2018;38:919-31. [Crossref] [PubMed]
- Khodanovich MY, Sorokina IV, Glazacheva VY, Akulov AE, Nemirovich-Danchenko NM, Romashchenko AV, Tolstikova TG, Mustafina LR, Yarnykh VL. Histological validation of fast macromolecular proton fraction mapping as a quantitative myelin imaging method in the cuprizone demyelination model. Sci Rep 2017;7:46686. [Crossref] [PubMed]
- Khodanovich M, Pishchelko A, Glazacheva V, Pan E, Akulov A, Svetlik M, Tyumentseva Y, Anan'ina T, Yarnykh V. Quantitative Imaging of White and Gray Matter Remyelination in the Cuprizone Demyelination Model Using the Macromolecular Proton Fraction. Cells 2019;8:E1204. [Crossref] [PubMed]
- Yarnykh VL, Prihod'ko IY, Savelov AA, Korostyshevskaya AM. Quantitative Assessment of Normal Fetal Brain Myelination Using Fast Macromolecular ProtonFraction Mapping. Am J Neuroradiol. 2018;39:1341-8. [Crossref] [PubMed]
- Korostyshevskaya AM, Prihod'ko IY, Savelov AA, Yarnykh VL. Direct comparison between apparent diffusion coefficient and macromolecular proton fraction as quantitative biomarkers of the human fetal brain maturation. J Magn Reson Imaging 2019;50:52-61. [Crossref] [PubMed]
- Korostyshevskaya AM, Savelov AA, Papusha LI, Druy AE, Yarnykh VL. Congenital medulloblastoma: Fetal and postnatal longitudinal observation with quantitative MRI. Clin Imaging 2018;52:172-6. [Crossref] [PubMed]
- Yarnykh V, Knipenberg N, Tereshchenkova O. Quantitative assessment of pediatric brain myelination in a clinical setting using macromolecular proton fraction. In: Proc 26th Annual Meeting ISMRM, Paris; 2018 (abstract 525).
- Marques JP, Simonis FFJ, Webb AG. Low-field MRI: An MR physics perspective. J Magn Reson Imaging 2019;49:1528-42. [Crossref] [PubMed]
- Naumova AV, Akulov AE, Khodanovich MY, Yarnykh VL. High-resolution three-dimensional macromolecular proton fraction mapping for quantitative neuroanatomical imaging of the rodent brain in ultra-high magnetic fields. Neuroimage 2017;147:985-93. [Crossref] [PubMed]
- Edelstein WA, Bottomley PA, Pfeifer LM. A signal-to-noise calibration procedure for NMR imaging systems. Med Phys 1984;11:180-5. [Crossref] [PubMed]
- Schneider CA, Rasband WS, Eliceiri KW. NIH Image to ImageJ: 25 years of image analysis. Nat Methods 2012;9:671-5. [Crossref] [PubMed]
- Vanderah TW, Gould DJ. Atlas of the Human Brainstem. In: Vanderah TW, Gould DJ, Nolte J. Nolte’s the human brain: an introduction to its functional anatomy. 7th edition. Elsevier, Philadelphia, 2016; 383-93.
- Underhill HR, Rostomily RC, Mikheev AM, Yuan C, Yarnykh VL. Fast bound pool fraction imaging of the in vivo rat brain: Association with myelin content and validation in the C6 glioma model. Neuroimage 2011;54:2052-65. [Crossref] [PubMed]
- MacKay A, Whittall K, Adler J, Li D, Paty D, Graeb D. In vivo visualization of myelin water in brain by magnetic resonance. Magn Reson Med 1994;31:673-7. [Crossref] [PubMed]
- Deoni SC, Rutt BK, Arun T, Pierpaoli C, Jones DK. Gleaning multicomponent T1 and T2 information from steady-state imaging data. Magn Reson Med 2008;60:1372-87. [Crossref] [PubMed]
- Hwang D, Kim DH, Du YP. In vivo multi-slice mapping of myelin water content using T2* decay. Neuroimage 2010;52:198-204. [Crossref] [PubMed]
- Lu J, Synowiec S, Lu L, Yu Y, Bretherick T, Takada S, Yarnykh V, Caplan J, Caplan M, Claud EC, Drobyshevsky A. Microbiota influence the development of the brain and behaviors in C57BL/6J mice. PLoS One 2018;13:e0201829. [Crossref] [PubMed]
- Goussakov I, Synowiec S, Yarnykh V, Drobyshevsky A. Immediate and delayed decrease of long term potentiation and memory deficits after neonatal intermittent hypoxia. Int J Dev Neurosci 2019;74:27-37. [Crossref] [PubMed]
- Yarnykh VL, Kisel AA, Khodanovich MY. Scan-Rescan Repeatability and Impact of B(0) and B(1) Field Nonuniformity Corrections in Single-Point Whole-Brain Macromolecular Proton Fraction Mapping. J Magn Reson Imaging 2020;51:1789-98. [Crossref] [PubMed]
- Mossahebi P, Yarnykh VL, Samsonov A. Analysis and correction of biases in cross-relaxation MRI due to biexponential longitudinal relaxation. Magn Reson Med 2014;71:830-8. [Crossref] [PubMed]
- Mossahebi P, Alexander AL, Field AS, Samsonov AA. Removal of cerebrospinal fluid partial volume effects in quantitative magnetization transfer imaging using a three-pool model with nonexchanging water component. Magn Reson Med 2015;74:1317-26. [Crossref] [PubMed]
- A G Teixeira RP, Neji R, Wood TC, Baburamani AA, Malik SJ, Hajnal JV. Controlled saturation magnetization transfer for reproducible multivendor variable flip angle T(1) and T(2) mapping. Magn Reson Med 2020;84:221-36. [Crossref] [PubMed]