Enhancement of the low resolution image quality using randomly sampled data for multi-slice MR imaging
Introduction
In in vivo MR imaging applications such as whole-body screening (1-11) and activation mapping in functional MRI (12-25), relatively low resolution MR imaging is often used due to the requirement of large field-of-view (FOV) or rapid imaging speed. The tradeoff for the shortened acquisition time in low resolution imaging is the dramatically reduced acquisition of high frequency components of MR signals. Images with lack of high frequency information provide limited details of the imaging objects. Recently, compressed sensing (CS) imaging technique (26,27) has been used to reduce the acquisition time and raw data size by significantly undersampling the k-space for MRI (28-50). Based on CS technique, the interpolated compressed sensing (iCS) MRI (51-53) is proposed and has demonstrated the advantages in multiple slice MR imaging acquisitions for improving image quality and contrast by utilizing the raw from other slices and the weighting functions. In this work, we investigate a novel strategy to improve image quality for multiple-slice low resolution imaging by using the sparse sampling technique. In a multiple-slice low resolution acquisition, on the top of the k-space data acquired for forming the low resolution image, more k-space data of one center slice will be acquired by using the incoherent sampling strategy. The extra k-space data of the center slice would be able to enhance the high frequency information and thus increase the image resolution, ultimately providing more detailed information of the image. Based on the low resolution data, weighting functions which reflect the difference between the center slice and other slices (or target slices) can be generated. The extra data acquired in the center slice will be interpolated to the other slices after multiplying the corresponding weighting functions. The image reconstruction for each slice will then be performed by using the CS reconstruction algorithm. This strategy is able to enhance the quality of the low resolution images in the multiple slice imaging, in terms of resolution, contrast and image fidelity. In vivo MR imaging of human brain was applied to investigate the feasibility and performance of the proposed method. Comparison with original low resolution images in image error was also performed.
Theory and methods
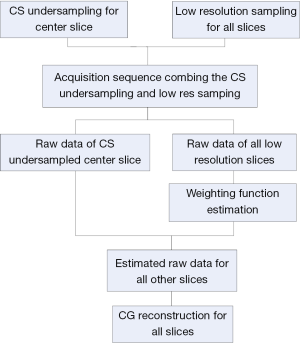
The proposed strategy for multiple-slice acquisition of the low resolution images is shown in Figure 1. To acquire the multiple-slice low resolution images together with the randomly undersampled k-space data of one center slice, we need to modify the conventional imaging sequences by adding sparse acquisition strategy to the center slice.
Firstly, the weighting functions between the center slice and the other slices are generated by calculating the quotient between the two images:
[1] |
where I1 and I2 denote the original low resolution images of the center slice and the other slices, respectively. By taking Fourier Transform the weighting functions in k-space domain are obtained:
[2] |
where Wk is the weighting function in k-space.
Secondly, the estimated k-space data of the target slice are calculated by taking convolution of the weighting function and the undersampled k-space data of the center slice:
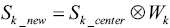 |
[3] |
where Sk_center is the raw data of the center slice undersampled by using sparse MRI strategy, while Sk_new is the estimated raw data of the target slice.
The final step is to interpolate these estimated data to the k-space of the original low resolution images of the target slices. By using nonlinear Conjugate Gradient (CG) reconstruction similar to that used in conventional CS MRI, an improved image with improved image resolution and lower image error can be obtained.
To validate the feasibility of the method, an acquisition example, capable of implementing the proposed method with human brain imaging was designed. The design procedure is shown in Figure 2. A total of 9 slices were acquired at low resolution. The extra randomly undersampled data were acquired for the center slice. These acquisitions (i.e., original low resolution and the extra data for the center slice) could be combined in one single imaging sequence and accomplished in a single acquisition. In image reconstruction, the weighting functions were calculated according to Eq. [1] and Eq. [2] and the high frequency k-space data of the other 8 slices were estimated by using the Eq. [3]. Finally, nonlinear CG method was used to perform image construction for all slices by using the estimated k-space data.
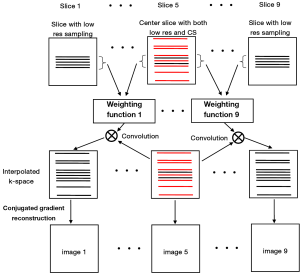
Image errors in the reference and undersampled images were calculated to evaluate reconstruction performance. The image errors were obtained by subtracting the reconstructed images from the full k-space reference images. Specifically, the image error calculation used was calculated by using:
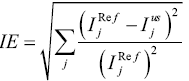 |
[4] |
where represents the signal intensity of the jth pixel in the full k-space reference images, and
represents the signal intensity of the jth pixel in the undersampled images reconstructed using the proposed method or the low resolution images.
In comparison studies, we performed image reconstruction using other two methods—zero filling method and conventional CS method at the same acquisition time (or the same undersampling rate) as that used in the proposed iCS acquisition. Image error maps and contrast to noise ratio (CNR) were compared to evaluate the performance of the three different methods.
Results
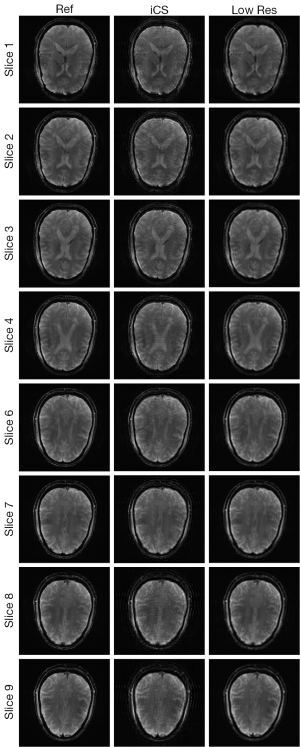
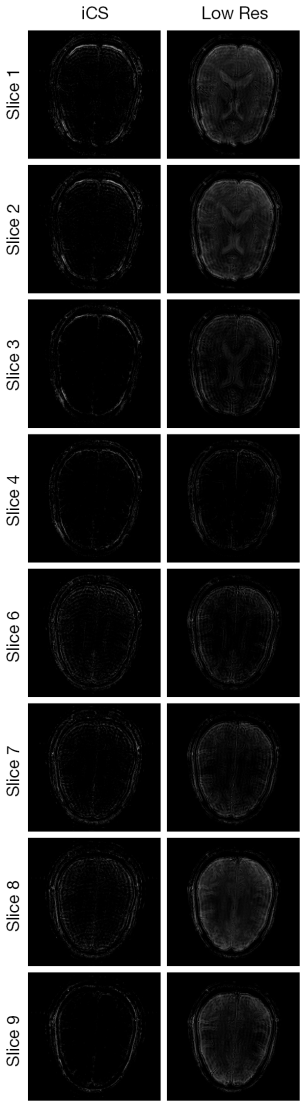
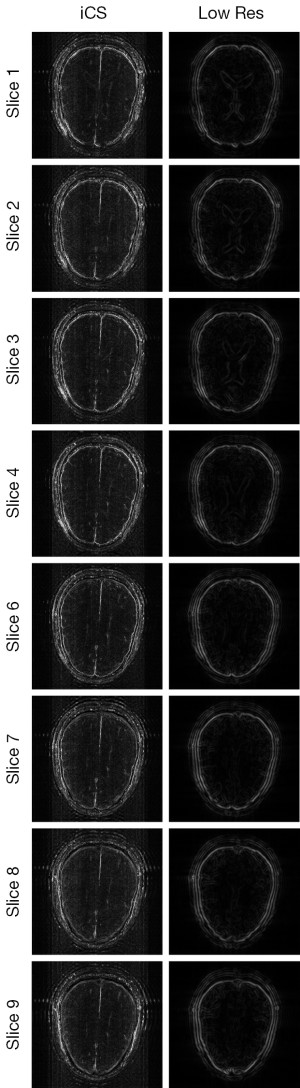
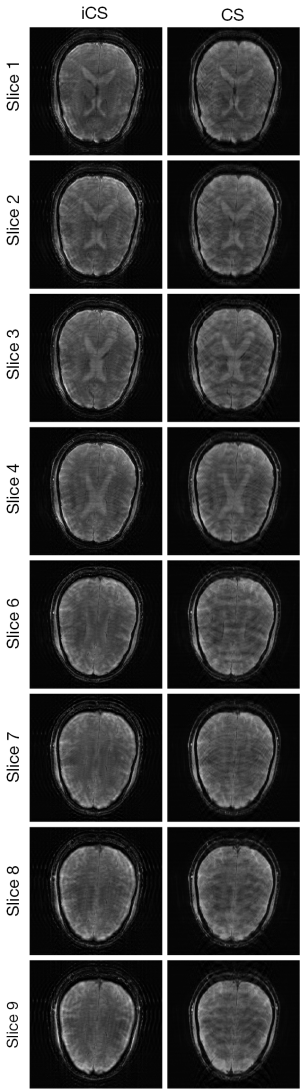
Figure 3 shows the human brain images of all the other 8 slices (except the center slice). The first column illustrates the images reconstructed from full k-space data (raw data size was 512 by 512) which serve as the reference images. The second column is the images reconstructed from the proposed method. The third column is the images reconstructed from the low resolution k-space data with 75 phase encoding steps which has an equivalent undersampling rate to the proposed method in this study. The number of phase encoding for iCS acquisition was 64, while the sparsely undersampling rate of the center slice was 1/4 in phase encoding direction (128 phase encoding). From the results shown in Figure 3, it is obvious that the image quality of the iCS method is higher than those of the same slice at low resolution acquisition. For quantitative evaluation and comparison, Eq. [4] was used to calculate the image errors for all slices. The residual images are show in Figure 4. The image errors for all the slices are shown in Table 1. These results demonstrate the significantly improved image fidelity of the proposed method.
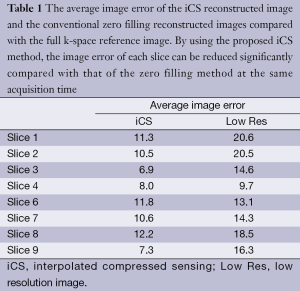
Full table
Figure 5 shows the CNR of the images shown in Figure 3. The average CNR of each image is shown in Table 2. From the CNR maps and Table 2 we can see that the CNR of the iCS images are much higher than that of the low resolution images at the same acquisition time.
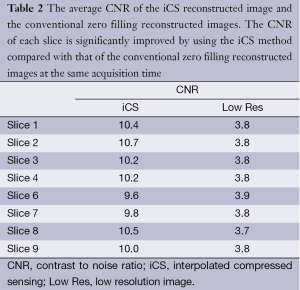
Full table
In the comparison with conventional CS method, undersampled images was acquired at the same acquisition time equivalent to that used for the iCS method, that is, the total phase encoding lines was 75 for each of the 9 slices in the multi-slice acquisition. By using the same conjugated gradient reconstruction strategy, conventional CS reconstructed images were obtained. The results of the comparison between the images reconstructed from the iCS method and conventional CS method for all the slices are shown in Figure 6. The average image error of conventional CS method was 14% larger than that using the proposed interpolated CS method. In addition, enlarged artifacts can be clearly observed in the images reconstructed using conventional CS. This further demonstrates the advantage of the proposed strategy in low resolution multiple-slice imaging.
Discussion and conclusions
A method for improving imaging quality in multi-slice low resolution imaging using iCS is proposed and investigated. The promising results in the in vivo human brain imaging validation and the comparison with the conventional imaging method at the same acquisition time have demonstrate the feasibility and advantages of the proposed method for multi-slice low resolution imaging. By acquiring extra sampling data of one center slice using the incoherent undersampling strategy in CS, more high frequency information in the k-space can be obtained in all slices, ultimately leading to improved images with higher CNR and spatial resolution. The proposed technique might directly benefit the imaging applications with the requirement of large FOV and/or fast acquisition.
In the proposed technique, the accuracy of the weighting function is critical to the accuracy of the interpolated k-space data and thus image fidelity. In generation of the weighting functions for interpolating the k-space data into the target slices, due to the finite Fourier transform and the noise generated during the scanning procedure, the weighting functions generated might not be accurate enough.
Acknowledgements
Funding: This work was partially supported by NIH grants EB008699, K99EB015487 and P41 EB013598, a QB3 Research Award, a Springer Med Fund Award, and a National Natural Science Foundation of China Grant (51228702).
Disclosure: The authors declare no conflict of interest.
References
- Padhani AR, Makris A, Gall P, et al. Therapy monitoring of skeletal metastases with whole-body diffusion MRI. J Magn Reson Imaging 2014;39:1049-78. [PubMed]
- Michielsen K, Vergote I, Op de Beeck K, et al. Whole-body MRI with diffusion-weighted sequence for staging of patients with suspected ovarian cancer: a clinical feasibility study in comparison to CT and FDG-PET/CT. Eur Radiol 2014;24:889-901. [PubMed]
- Del Vescovo R, Frauenfelder G, Giurazza F, et al. Role of whole-body diffusion-weighted MRI in detecting bone metastasis. Radiol Med 2014. [Epub ahead of print]. [PubMed]
- Wu X, Nerisho S, Dastidar P, et al. Comparison of different MRI sequences in lesion detection and early response evaluation of diffuse large B-cell lymphoma--a whole-body MRI and diffusion-weighted imaging study. NMR Biomed 2013;26:1186-94. [PubMed]
- Kwee TC, Vermoolen MA, Akkerman EA, et al. Whole-body MRI, including diffusion-weighted imaging, for staging lymphoma: Comparison with CT in a prospective multicenter study. J Magn Reson Imaging 2013. [Epub ahead of print]. [PubMed]
- Jouvet JC, Thomas L, Thomson V, et al. Whole-body MRI with diffusion-weighted sequences compared with 18 FDG PET-CT, CT and superficial lymph node ultrasonography in the staging of advanced cutaneous melanoma: a prospective study. J Eur Acad Dermatol Venereol 2013. [Epub ahead of print]. [PubMed]
- Akbarzadeh A, Ay MR, Ahmadian A, et al. MRI-guided attenuation correction in whole-body PET/MR: assessment of the effect of bone attenuation. Ann Nucl Med 2013;27:152-62. [PubMed]
- Mürtz P, Kaschner M, Träber F, et al. Diffusion-weighted whole-body MRI with background body signal suppression: technical improvements at 3.0 T. J Magn Reson Imaging 2012;35:456-61. [PubMed]
- Koh DM, Blackledge M, Padhani AR, et al. Whole-body diffusion-weighted MRI: tips, tricks, and pitfalls. AJR Am J Roentgenol 2012;199:252-62. [PubMed]
- Horger M, Weisel K, Horger W, et al. Whole-body diffusion-weighted MRI with apparent diffusion coefficient mapping for early response monitoring in multiple myeloma: preliminary results. AJR Am J Roentgenol 2011;196:W790-5. [PubMed]
- Fischer MA, Nanz D, Hany T, et al. Diagnostic accuracy of whole-body MRI/DWI image fusion for detection of malignant tumours: a comparison with PET/CT. Eur Radiol 2011;21:246-55. [PubMed]
- Uğurbil K, Xu J, Auerbach EJ, et al. Pushing spatial and temporal resolution for functional and diffusion MRI in the Human Connectome Project. Neuroimage 2013;80:80-104. [PubMed]
- De Martino F, Schmitter S, Moerel M, et al. Spin echo functional MRI in bilateral auditory cortices at 7 T: an application of B1 shimming. Neuroimage 2012;63:1313-20. [PubMed]
- Chen W, Liu X, Zhu XH, et al. Functional MRI study of brain function under resting and activated states. Conf Proc IEEE Eng Med Biol Soc 2009;2009:4061-3.
- Liu X, Tian W, Kolar B, et al. Advanced MR diffusion tensor imaging and perfusion weighted imaging of intramedullary tumors and tumor like lesions in the cervicomedullary junction region and the cervical spinal cord. J Neurooncol 2014;116:559-66. [PubMed]
- Wu Y, Zou C, Liu W, et al. Effect of B-value in revealing postinfarct myocardial microstructural remodeling using MR diffusion tensor imaging. Magn Reson Imaging 2013;31:847-56. [PubMed]
- Chan KC, Khong PL, Lau HF, et al. Late measures of microstructural alterations in severe neonatal hypoxic-ischemic encephalopathy by MR diffusion tensor imaging. Int J Dev Neurosci 2009;27:607-15. [PubMed]
- Guo AC, Jewells VL, Provenzale JM. Analysis of normal-appearing white matter in multiple sclerosis: comparison of diffusion tensor MR imaging and magnetization transfer imaging. AJNR Am J Neuroradiol 2001;22:1893-900. [PubMed]
- Saito K, Ledsam J, Sourbron S, et al. Measuring hepatic functional reserve using low temporal resolution Gd-EOB-DTPA dynamic contrast-enhanced MRI: a preliminary study comparing galactosyl human serum albumin scintigraphy with indocyanine green retention. Eur Radiol 2014;24:112-9. [PubMed]
- Scouten A, Papademetris X, Constable RT. Spatial resolution, signal-to-noise ratio, and smoothing in multi-subject functional MRI studies. Neuroimage 2006;30:787-93. [PubMed]
- Damon BM, Wadington MC, Lansdown DA, et al. Spatial heterogeneity in the muscle functional MRI signal intensity time course: effect of exercise intensity. Magn Reson Imaging 2008;26:1114-21. [PubMed]
- Hanakawa T, Dimyan MA, Hallett M. Motor planning, imagery, and execution in the distributed motor network: a time-course study with functional MRI. Cereb Cortex 2008;18:2775-88. [PubMed]
- Damon BM, Wadington MC, Hornberger JL, et al. Absolute and relative contributions of BOLD effects to the muscle functional MRI signal intensity time course: effect of exercise intensity. Magn Reson Med 2007;58:335-45. [PubMed]
- Zhang X, Yacoub E, Hu X. New strategy for reconstructing partial-Fourier imaging data in functional MRI. Magn Reson Med 2001;46:1045-8. [PubMed]
- Monk CS, Zhuang J, Curtis WJ, et al. Human hippocampal activation in the delayed matching- and nonmatching-to-sample memory tasks: an event-related functional MRI approach. Behav Neurosci 2002;116:716-21. [PubMed]
- Donoho DL. Compressed sensing. IEEE Trans Inform Theory 2006;52:1289-306.
- Tsaig Y, Donoho DL. Extensions of compressed sensing. Signal Processing 2006;86:533-48.
- Lustig M, Donoho D, Pauly JM. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magn Reson Med 2007;58:1182-95. [PubMed]
- Wu B, Li W, Guidon A, et al. Whole brain susceptibility mapping using compressed sensing. Magn Reson Med 2012;67:137-47. [PubMed]
- Madelin G, Chang G, Otazo R, et al. Compressed sensing sodium MRI of cartilage at 7T: preliminary study. J Magn Reson 2012;214:360-5. [PubMed]
- Yu Y, Hong M, Liu F, et al. Compressed sensing MRI using Singular Value Decomposition based sparsity basis. Conf Proc IEEE Eng Med Biol Soc 2011;2011:5734-7.
- Wu B, Millane RP, Watts R, et al. Prior estimate-based compressed sensing in parallel MRI. Magn Reson Med 2011;65:83-95. [PubMed]
- Michailovich O, Rathi Y, Dolui S. Spatially regularized compressed sensing for high angular resolution diffusion imaging. IEEE Trans Med Imaging 2011;30:1100-15. [PubMed]
- Majumdar A, Ward RK. An algorithm for sparse MRI reconstruction by Schatten p-norm minimization. Magn Reson Imaging 2011;29:408-17. [PubMed]
- Liang D, DiBella EV, Chen RR, et al. k-t ISD: dynamic cardiac MR imaging using compressed sensing with iterative support detection. Magn Reson Med 2012;68:41-53. [PubMed]
- Menzel MI, Tan ET, Khare K, et al. Accelerated diffusion spectrum imaging in the human brain using compressed sensing. Magn Reson Med 2011;66:1226-33. [PubMed]
- Larson PE, Hu S, Lustig M, et al. Fast dynamic 3D MR spectroscopic imaging with compressed sensing and multiband excitation pulses for hyperpolarized 13C studies. Magn Reson Med 2011;65:610-9. [PubMed]
- Çukur T, Lustig M, Saritas EU, et al. Signal compensation and compressed sensing for magnetization-prepared MR angiography. IEEE Trans Med Imaging 2011;30:1017-27. [PubMed]
- Huang F, Lin W, Duensing GR, et al. K-t sparse GROWL: sequential combination of partially parallel imaging and compressed sensing in k-t space using flexible virtual coil. Magn Reson Med 2012;68:772-82. [PubMed]
- Hong M, Yu Y, Wang H, et al. Compressed sensing MRI with singular value decomposition-based sparsity basis. Phys Med Biol 2011;56:6311-25. [PubMed]
- Vasanawala SS, Alley MT, Hargreaves BA, et al. Improved pediatric MR imaging with compressed sensing. Radiology 2010;256:607-16. [PubMed]
- Chang CH, Ji J. Improved compressed sensing MRI with multi-channel data using reweighted l(1) minimization. Conf Proc IEEE Eng Med Biol Soc 2010;2010:875-8.
- Ajraoui S, Lee KJ, Deppe MH, et al. Compressed sensing in hyperpolarized 3He lung MRI. Magn Reson Med 2010;63:1059-69. [PubMed]
- Hu S, Lustig M, Balakrishnan A, et al. 3D compressed sensing for highly accelerated hyperpolarized (13)C MRSI with in vivo applications to transgenic mouse models of cancer. Magn Reson Med 2010;63:312-21. [PubMed]
- Holland DJ, Malioutov DM, Blake A, et al. Reducing data acquisition times in phase-encoded velocity imaging using compressed sensing. J Magn Reson 2010;203:236-46. [PubMed]
- Haldar JP, Hernando D, Liang ZP. Compressed-sensing MRI with random encoding. IEEE Trans Med Imaging 2011;30:893-903. [PubMed]
- Otazo R, Kim D, Axel L, et al. Combination of compressed sensing and parallel imaging for highly accelerated first-pass cardiac perfusion MRI. Magn Reson Med 2010;64:767-76. [PubMed]
- Liang D, Liu B, Wang J, et al. Accelerating SENSE using compressed sensing. Magn Reson Med 2009;62:1574-84. [PubMed]
- Ji JX, Zhao C, Lang T. Compressed sensing parallel magnetic resonance imaging. Conf Proc IEEE Eng Med Biol Soc 2008;2008:1671-4.
- Hu S, Lustig M, Chen AP, et al. Compressed sensing for resolution enhancement of hyperpolarized 13C flyback 3D-MRSI. J Magn Reson 2008;192:258-64. [PubMed]
- Pang Y, Zhang X. Interpolated compressed sensing for 2D multiple slice fast MR imaging. PLoS One 2013;8:e56098. [PubMed]
- Pang Y, Zhang X. Interpolated Compressed Sensing MR Image Reconstruction using Neighboring Slice k-space Data. Proc Intl Soc Mag Reson Med 2012;2275.
- Pang Y, Jiang J, Zhang X. Ultrafast Fetal MR Imaging using Interpolated Compressed Sensing. Proc Intl Soc Mag Reson Med 2014;2224.


