Error decomposition for parallel imaging reconstruction using modulation-domain representation of undersampled data
Introduction
Since the development of radiofrequency (RF) coil array (1), parallel imaging has been clinically used to accelerate data acquisition for reduced imaging time or improved temporal/spatial resolution (2-6) in magnetic resonance imaging (MRI). The mechanism underlying this technique is that multi-channel coil sensitivity provides spatial encoding information that can be used to reconstruct a full field of view (FOV) image from data sampled below the Nyquist limit. In principle, a coil array with more elements gives better spatial encoding capability, thereby allowing for a higher undersampling factor in parallel imaging. With the advancement of high channel count coil array (7-10), parallel imaging with an undersampling factor of four or higher has been demonstrated in research studies (11-22). In clinical diagnosis and treatment, however, most clinical MRI scans for patient examination are accelerated by a factor of only two or even lower. This implies that currently available parallel imaging techniques for clinical use cannot take full advantage of coil array encoding capability, indicating the needs for a quantitative approach to optimizing parallel imaging for clinical applications. Indeed, although recent years have seen the development of a number of parallel imaging techniques (11-13,15,19,23-29), their clinical imaging performance has not been extensively investigated. Today clinical evaluation of parallel imaging is still an open issue.
To evaluate and optimize parallel imaging, a clear definition of clinical imaging quality is needed. Unfortunately, as clinical applications of MRI are diversified, image quality has a number of widely different interpretations depending on what information is needed for clinical diagnosis or treatment. For example, cancer imaging requires high fidelity in image contrast for tumor diagnosis (30-32). In cardiac imaging, as imaging artifacts (e.g., from motion) may considerably compromise cardiovascular information (33,34), lower artifacts means better image quality. In spectroscopy, signal to noise ratio (SNR) is a primary factor that determines image quality (35,36). Due to this diversity, it is difficult to use the same criterions for imaging quality evaluation in every MRI application, suggesting that optimal parallel imaging may be application dependent.
Another issue in parallel imaging evaluation is the complexity of an image reconstruction error. It has been known that parallel imaging reconstruction contains multiple error components. For example, artifacts may be caused by insufficient spatial encoding of coil sensitivity, and noise may be amplified in reconstruction. To date, the only error component that has been clearly defined is “geometric factor” (g-factor) that quantifies noise amplification. Since the definition of this concept (3), it has become a standard to assess parallel imaging (7-9,11,37). It is of no doubt that noise suppression is important to parallel imaging. However, as noise is not always crucial to clinical imaging, other error components, such as aliasing artifacts, must be taken into account. In addition, it has been noticed that the suppression of an error component in reconstruction may lead to the increase of other error components, implying there exist tradeoffs between error components (38). No further effort has been made by far to investigate how these tradeoffs may affect parallel imaging.
The presented work provides an engineering approach to evaluating and optimizing parallel imaging for a clinical requirement that may be quantified by an error function. Here parallel imaging reconstruction is considered as a linear system. A new concept, “modulation domain”, is introduced for the development of a linear k-space parallel imaging error model. By representing undersampled data in modulation domain, reconstruction error may be decomposed into multiple error components that can be grouped into three different categories, which are called “image fidelity error”, “residue aliasing artifacts”, and “amplified noise” respectively in the presented work. It is experimentally found these error components have different image-space patterns that affect image quality in different fashions. Accordingly, an error function may be defined as the weighted summation of these error components. By utilizing a set of weightings that can characterize a clinical requirement, e.g., the best image fidelity in a region of clinical interest, parallel imaging may be evaluated and optimized quantitatively. This error decomposition model will enable application-oriented reconstruction for improved clinical performance of parallel imaging.
Materials and methods
In parallel imaging, data acquisition is accelerated by undersampling in the phase encoding direction. This requires a special reconstruction algorithm that combines undersampled data from multi-channel coil array and generates a full FOV image with minimal loss of clinical information. To optimize reconstruction, an error function is needed for quantifying the information loss. This section gives a theoretical description of the proposed error decomposition model for parallel imaging. Also presented is how to use this model to define an error function that can evaluate the loss of clinical information. For notation simplicity, only the mathematical equations for 2D parallel imaging are provided. With minor modification of notation, they may be used generically in 3D or dynamic imaging.
Parallel imaging error model in k-space
Parallel imaging reconstruction can be represented by the weighted summation of multi-channel images in image space (19,20,39). In principle, the weighting coefficients for every channel are dependent on multi-channel coil sensitivity (3,12,19), implying these coefficients in image space are as smooth as coil sensitivity. It is reasonable to use low-pass filters to model parallel imaging reconstruction in k-space. As shown in Figure 1, data filtering forms the primary signal path in k-space model. The other signal path is the noise amplification of reconstruction filters. This noise amplification is called “g-factor” in literature (3,37). The model output in Figure 1 is a reconstruction error defined as the difference between the reconstructed and target image data.
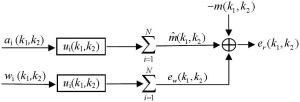
Modulation-domain representation of undersampled data
Uniformly undersampled data can be mathematically represented as the modulation of fully-sampled data with a function fm(k1,k2) given by:
[1] |
where R is the reduction factor in undersampling, i.e., the acceleration factor, k1 is the phase encoding line index, and k2 is the frequency encoding data index. As the function fm(k1,k2) equals unity if k1 is a multiple of the reduction factor and zero otherwise, the modulation of full k-space data with this function keeps one of every R phase encoding lines and zero the others, resulting in the same partial k-space data as those collected in parallel imaging. This mathematical representation of undersampling operation is termed as “modulation-domain representation” in the presented work. As illustrated by Figure 2, a set of undersampled data may be decomposed into R different components in modulation domain: one is the original fully-sampled data and the others are the fully-sampled data modulated by a series of harmonics with normalized frequencies equal to n/R, n=1, 2,…, R-1.
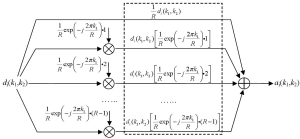
Error decomposition in parallel imaging reconstruction using modulation-domain representation
The k-space model in Figure 1 can be transformed to modulation domain by replacing the undersampled data with the modulation-domain representation in Figure 2. As summation and convolution are interchangeable in a linear system, a k-space model (Figure 3) equivalent to Figure 1 can be generated. In this model, the total reconstruction error er(k1,k2) is decomposed into multiple error components:
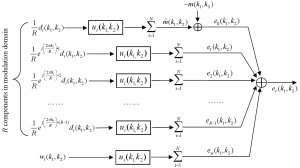
[2] |
and
[3] |
where “*” represent the convolution, {di(k1,k2)}i=1, 2, …, N are fully sampled data, {ui(k1,k2)}i=1, 2, …, N are reconstruction filters, m(k1,k2) represents the target image data, and {wi(k1,k2)}i=1, 2, …, N are the noise from data acquisition. In Eq. [3], it can be seen that the error components, {en(k1,k2)}n=0, 1, 2, …, R-1, are generated from the R modulation-domain components. They are accordingly called “modulation-domain error” in this work.
Modulation-domain error components can be grouped into two categories: the first category includes one error component, e0, which is the difference between the target image data and the sum of filtered fully-sampled data. This error component quantifies how well the original image information is preserved by reconstruction filters and is thus called “image fidelity error”. The other error components, e1, e1, …, eR-1, are in the second category. They can be considered as the modulation of fully-sampled data with a series of different harmonics. By inverse Fourier transform, one can find that this modulation introduces image-space shifts equal to n/R of FOV (n=1, 2,…, R-1) in the phase encoding direction, indicating these modulated data generate aliasing. Reconstruction filters are designed to zero these aliasing and these error components represent residue aliasing after data filtering. They are accordingly called “residue aliasing artifacts” in this work.
Error function with weightings on error components
Parallel imaging techniques are typically designed to minimize the total reconstruction error {er in Eq. [2]}. This cannot address the needs of clinical imaging well for two reasons: first, a single quantity cannot cover a wide range of diversified clinical requirements; second, the total reconstruction error is the mix of multiple error components that affect image quality differently. As a result, most parallel imaging techniques give a sub-optimal solution to clinical applications. Using error decomposition, an error function may be defined as the weighted summation of different error components. This allows for quantification of different clinical requirements by choosing different combinations of weightings in the error function. By minimizing a defined error function, image reconstruction can be optimized for a clinical requirement, providing an “application-oriented” approach to parallel imaging. Apparently, there exist multiple ways to define this error function. For the purpose of concept demonstration, the presented work uses the following one:
[4] |
where α, β, and λ are the weighting coefficients for image fidelity error, residue aliasing artifacts and amplified noise. These weighting coefficients evaluate the relative significance of each error component in terms of a clinical requirement: a higher weighting on one error component means higher significance and leads to more suppression of that component, but less suppression of other components.
In image space, the error function defined by Eq. [4] becomes:
[5] |
where Ei’s (i=0, 1, 2, …, R-1) and Ew are inverse Fourier transforms of ei’s and ew in Eq. [3], and (r1, r2) represents the position indexes in image space. As inverse Fourier transform converts k-space convolution to image-space multiplication, image-space error function is pixel-wise.
Practical solution to reconstruction
The minimization of an error function in Eq. [4] or Eq. [5] requires the partial derivative of εss with respect to the conjugate of the reconstruction filters {ui(k1,k2)}i=1, 2, …, N be equal to zero. This generates a set of linear equations: the unknowns are the reconstruction filters and the coefficients are dependent on the fully-sampled data {di(k1,k2)}i=1, 2, …, N, the target image data m(k1,k2), and the noise data {wi(k1,k2)}i=1, 2, …, N. Practically in a MRI scan, fully sampled data may use low-resolution calibration data acquired either from pre-scan or from auto-calibration signals (ACS). The target image data can be generated from the low-resolution data: they can be either the data from a single channel (channel by channel reconstruction), or the data for a composite image, e.g., sum of square image. The noise data can be estimated from a noise scan. The solution to reconstruction can be found either in k-space using Eq. [4] or in image space using Eq. [5].
Data acquisition
The human imaging experiments in this work were conducted in compliance with the regulations of the institution’s human ethics committee. The following experiments were used to demonstrate the presented approach:
- A set of axial brain images was collected on a 3.0 T GE scanner using T1 FLAIR sequence (FOV 220×220 mm, matrix size 512×512, TR 3,060 ms, TE 126 ms, flip angle 90°, slice thickness 5 mm, number of averages 1). The phase encoding direction was left-right. The coil was an 8-channel head coil.
- A set of cardiac function images was collected on a 1.5 T SIEMENS scanner using a cine true FISP sequence (FOV 340×255 mm, matrix size 384×150, TR 20.02 ms, TE 1.43 ms, flip angle 46°, slice thickness 6 mm, number of averages 1). The phase encoding direction was anterior-posterior. The coil was a 12-channel cardiac coil array.
- A set of breast images was collected on a 1.5 T SIEMENS scanner using a turbo spin-echo sequence (FOV 340×340 mm, matrix size 196×384, TR 750 ms, TE 1.6 ms, slice thickness 1 mm, number of averages 1). The phase encoding direction was left-right. The coil was a 12-channel breast coil.
- A set of saggital cervical spine images was collected on a 3.0 T PHILIPS scanner using a T2-weighted multi-slice turbo spin-echo sequence (FOV 160×248 mm, matrix size 200×248, TR 3,314 ms, TE 120 ms, slice thickness 3 mm, flip angle 90°, echo train length =16, interleaving factor 4). The phase encoding direction was superior-inferior. The coil was a 16-element neurovascular coil array.
Parallel imaging reconstruction
Data were fully sampled in all the experiments. Partial k-space data were generated by down-sampling in the phase encoding direction during post-processing. The presented reconstruction, if not specified, were generated with 24 ACS lines in calibration. The reconstruction algorithms were implemented in MATLAB® (MathWorks Inc., Natick, MA, USA). Channel by channel reconstruction was used. The images from fully-sampled data were used as references. In the presented results, an error image is the difference between the reconstructed and reference images. The Root of the Sum of Squares (RSS) error is defined as the square RSS of the error image. This error is normalized with respect to the reference image, i.e., RSS error represents the ratio (in percentage) of the RSS of the error image to that of the reference image.
Results
Image-space pattern of different error components
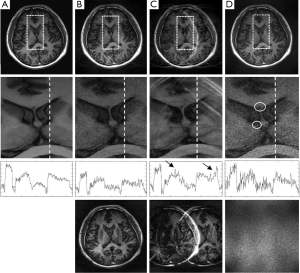
If an error function given by Eq. [4] or [5] is minimized, weighting coefficients, α, β, and λ, play a role of balancing different error components in the reconstructed image. In an extreme case, i.e., when a weighting coefficient is much smaller than the others, one error component will be dominant. Figure 4 shows the reconstruction results of three extreme cases using the brain imaging data with a reduction factor of 4. In the first case (Figure 4B) where image fidelity error is dominant, the reconstructed images give low artifacts and noise. However, by comparing the one dimensional (1D) intensity plots along the projection line (dashed line) in the enlarged center-region images, it can be seen that there exists considerable distortion in image contrast (image intensity differences in different tissues). In the second case (Figure 4C) where the residue aliasing artifacts are dominant, the error is concentrated in local regions. In the plot that shows 1D image intensity along the projection line, these artifacts manifest as sharp peaks (marked by arrows). In the third case (Figure 4D) where the amplified noise is dominant, the reconstructed image shows high variation of image intensity. This noisy feature can be easily seen in the enlarged center-region image and the 1D intensity plot along the projection line. Typically, the amplified noise reduces SNR, resulting in loss of image details, as in the circled regions of Figure 4D. From the error images, it can be seen that the image-space patterns of three error components are different: image fidelity error is global and follows the original image patterns; residue aliasing artifacts are localized and can be destructive; amplified noise randomly spreads over the entire image space with a “patterned” power distribution (related to g-factor). These different patterns may introduce loss of different clinical information in reconstruction. Practically, three image-space patterns coexist and have tradeoffs, introducing complicated noise or artifact behaviors in image space. The following experimental work will be focused on whether these tradeoffs can be controlled by adjusting the weightings on different error components in an error function.
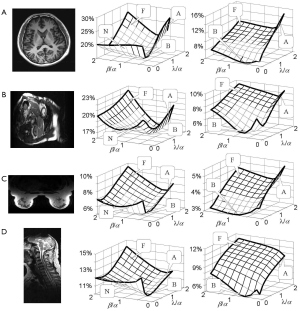
Dependence of RSS error on weighting coefficients in error function
RSS error is a “total reconstruction error” that has been the primary target to be minimized in most parallel imaging techniques (19-23,26). Figure 5 shows an experimental investigation on how RSS error changes with the weighting coefficients α, β, and λ, if the error function in Eq. [4] is minimized. Four datasets acquired from the brain, cardiac, breast, and spine imaging experiments were used. Parallel imaging reconstruction was implemented with a high (R =4) and a low (R =2) reduction factor. From the 3D plots of the calculated RSS error against the weighting coefficient ratios β/α and λ/α, it can be seen that the plots for a high reduction factor have three high-RSS-error regions corresponding to the three extreme cases given by Figure 4. Here three capital letters, “F”, “A”, and “N” are used to indicate the three regions where “image fidelity error”, “residue aliasing artifacts”, and “amplified noise” are respectively dominant. A valley surrounded by “N”, “F” and “A” regions can be seen. In this valley region, all error components are well balanced and the RSS error is minimal. A letter “B” that represents “balanced” is used to indicate this region. Compared with the plots for a high reduction factor, those for a low reduction factor do not have a clear “N” region, indicating that image fidelity error and residue aliasing artifacts dominate the RSS error. This is reasonable because SNR is high in data acquisition with a low reduction factor and noise amplification is trivial. Consequently, RSS error relies primarily on the balance of image fidelity error and residue aliasing artifacts. Furthermore, it is found that the weighting coefficients for “B” region vary largely with data differences. The error function in Eq. [4] provides an approach to minimizing the RSS error empirically by locating the “B” region in 3D plots given by Figure 5.
Spatially different weighting coefficients in error function
The pixel-wise image-space error function in Eq. [5] can quantify local information loss in image space, providing an approach to optimizing reconstruction in a region of interest smaller than the FOV. Assuming the clinical significance of all error components in the region of interest is known, the following spatially different weighting coefficients may be used to define an error function in Eq. [5]:
[6] |
where ROI represents the “region of interest” in image space, and the parameters αROI, βROI, λROI, α0, β0, and λ0 will be determined from priori knowledge.
Figure 6A gives an example of image reconstruction from brain imaging data using spatially different weighting coefficients. In this reconstruction, the rectangular box is defined as an ROI. It is assumed that there is a clinical need for more suppression of residue aliasing artifacts in the ROI than that in Figure 6B. In this example, the weighting coefficients outside the ROI, α0, β0, and λ0, are kept the same as those in Figure 6B. Inside the ROI, we let αROI = α0, βROI =1.5β0, and λROI = λ0. By comparing Figure 6A-C, it can be seen that spatially different weighting coefficients improve SNR without considerable increase of residue aliasing artifacts in the ROI. Although this improvement introduces a slight increase in RSS error, the image quality inside the ROI is better. From the error images in Figure 6A,B, it can be seen that the reduction of residue aliasing artifacts in the ROI is associated with the increase of image fidelity error outside the ROI, implying that the reconstruction in Figure 6A achieves low artifact level in the ROI by trading the image fidelity error outside the ROI. Therefore, error decomposition offers the ability to balance reconstruction errors across regions in image space using spatially different weightings. This is useful in clinical imaging that requires the preservation of clinical information within a region of interest smaller than the FOV.

Determination of weighting coefficients without priori knowledge
Practically, ROI information is not always known. It is desirable to calculate weighting coefficients from the acquired data. A solution to automatic weightings can be found using the error-decomposition model in Figure 3. In this model, different error components are generated respectively from original images, modulated versions of original images, and noise. These signal sources go through the same reconstruction filters before final combination. The reconstruction filters play a role to maximally suppress the modulated versions of original images and noise with minimal distortion of the original images. From this perspective, the relative signal strength of original images, their modulated versions, and noise level, are the natural quantities to weight the error components in reconstruction. It is sensible that an error component needs more suppression in reconstruction if it is generated from a stronger signal source. Since only relative ratios of these weighting coefficients matter, image fidelity error and residue aliasing artifacts may be weighted by the relative signal strength of original images and their modulated versions with respect to the noise level, i.e., the SNRs in original images and their modulated versions. Practically, the calibration data can be used to estimate SNRs. One may calculate SNRs of composite images, e.g., sum of square images, using Roemer’s method (1). Alternatively, one may calculate SNRs from phase image because phase variation decreases as SNR increases and the reciprocal of local phase variation in image space evaluates SNR level (40). Compared with the direct calculation of SNRs using Roemer’s method, phase variation is more robust because it is not sensitive to absolute image intensities that may vary largely in different clinical applications.
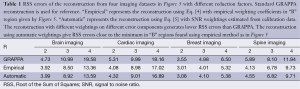
Figure 6D shows an example of reconstruction from brain imaging data using SNRs calculated from phase image as weightings in the error function. This reconstruction in the region of interest is comparable to Figure 6A which uses weightings obtained from priori knowledge. Table 1 summarizes a series of experiments with the brain, cardiac, breast, and spine imaging data. It can be seen that the reconstruction using estimated SNRs as weightings gives RSS errors close to the minimum which can be achieved by seeking “B” regions empirically from the 3D plots in Figure 5.
Full table
Reconstruction with higher undersampling factors and less calibration data
Typically, a brain imaging protocol on a clinical MRI system with an 8-channel head coil uses 4 as the upper limit of acceleration factor and 24 as the default ACS lines for parallel imaging. This work investigates whether error decomposition can improve parallel imaging reconstruction when a high undersampling factor (>4) or a small number of ACS lines (<24) is used. In this experiment, it was found a conventional technique, such as GRAPPA, gives destructive aliasing artifacts or high noise when only 12 ACS lines or a reduction factor of 5 is used Figure 7A,B. In contrast, the reconstruction using automatic SNR weightings with error decomposition performs well (Figure 7C,D), suggesting the presented technique can enhance acceleration capability of parallel imaging.
Discussion
What can be optimized from RSS error minimization?
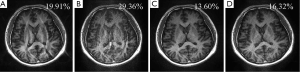
RSS error has been widely used in parallel imaging reconstruction. This work indicates that RSS error may not be a good quantity to evaluate local information loss that critically affects clinical imaging performance. The experiment in Figure 6 gives an example. In GRAPPA reconstruction (Figure 6C), noise amplification is high, which is reasonable because of the lack of noise regularization. Figure 6B shows a reconstruction result using Eq. [4] with the weighting coefficients in the “B” region of the 3D plot given by Figure 5. This reconstruction gives a much lower RSS error (13.36%) than GRAPPA (19.58%). From the enlarged center-region and error images in Figure 6B,C, it can be seen that GRAPPA gives lower SNR while the reconstruction with the minimum RSS error gives higher residue aliasing artifacts (marked by arrows), implying residue aliasing artifacts are traded for SNR in this optimization. This can effectively reduce the RSS error because RSS error is more dependent on global noise than on localized aliasing artifacts. It is obvious that aliasing artifacts are more destructive than noise if they appear in the region of interest due to their higher concentration of energy. For this r;on, RSS error can be misleading in clinical imaging.
In clinical applications, including brain, cardiac, breast, or spine imaging, the region of interest is typically a small part of FOV. The image quality over the entire FOV is not as important as that of the ROI in many clinical cases. From this perspective, the minimization of RSS error is not equivalent to the preservation of clinical information. Since most parallel imaging techniques are designed to minimize RSS errors, their clinical performance seems to be sub-optimal. This has been a reason why the speed of clinical imaging is lower that what has been demonstrated in research.
Evaluation of reconstruction methods
Error decomposition may be used to evaluate the performance of a reconstruction technique. By comparing multiple error components, the presented modulation-domain model {Eq. [3] and Figure 3} provides a better view of image information loss than RSS error in reconstruction. An example of such evaluation is shown in Figure 8. In this example, GRAPPA (4) and regularized SENSE (41) are compared using the brain imaging data. Using RSS error, the difference between these two methods is not significant. However, if three different error components are compared respectively using Eq. [3], it can be seen that GRAPPA gives lower image fidelity error, but higher residue aliasing artifacts and amplified noise, than the regularized SENSE. Therefore, GRAPPA performs better if image contrast is important while the regularized SENSE gives a better solution if aliasing and noise are destructive. This is valuable to clinical imaging because it can be used to assist the selection of appropriate parallel imaging techniques based on a clinical requirement.

Summary
In this study, the total reconstruction error of parallel imaging is decomposed into multiple error components based on a modulation-domain representation of undersampled data. These error components can be grouped into three categories: image fidelity error, residue aliasing artifacts, and amplified noise. The error decomposition allows for the use of different weightings on different error components to define an error function for the optimization of reconstruction. As these error components compromise image quality differently, this weighting approach can optimize parallel imaging in several ways:
- By empirically adjusting weighting coefficients, the error components can be balanced to minimize RSS error that evaluates the global imaging quality;
- Using spatially different weightings obtained from priori information, the reconstruction can be optimized for a region of clinical interest smaller than the FOV;
- Spatially different weighting coefficients can be automatically calculated from calibration data for image space reconstruction, providing a solution close to the optimum parallel imaging reconstruction.
The error decomposition can also quantify clinical information loss in reconstruction, providing a better approach to evaluating a parallel imaging technique than RSS error. It is expected that this work will improve the clinical utility of parallel imaging and enhance its acceleration capability in a wide spectrum of clinical applications.
Acknowledgements
This work is supported in part by national institute of health under the award number NIH R21 HD071540.
Disclosure: The author declares no conflict of interest.
References
- Roemer PB, Edelstein WA, Hayes CE, et al. The NMR phased array. Magn Reson Med 1990;16:192-225. [PubMed]
- Sodickson DK, Manning WJ. Simultaneous acquisition of spatial harmonics (SMASH): fast imaging with radiofrequency coil arrays. Magn Reson Med 1997;38:591-603. [PubMed]
- Pruessmann KP, Weiger M, Scheidegger MB, et al. SENSE: sensitivity encoding for fast MRI. Magn Reson Med 1999;42:952-62. [PubMed]
- Griswold MA, Jakob PM, Heidemann RM, et al. Generalized autocalibrating partially parallel acquisitions (GRAPPA). Magn Reson Med 2002;47:1202-10. [PubMed]
- Tsao J, Boesiger P, Pruessmann KP. k-t BLAST and k-t SENSE: dynamic MRI with high frame rate exploiting spatiotemporal correlations. Magn Reson Med 2003;50:1031-42. [PubMed]
- Huang F, Akao J, Vijayakumar S, et al. k-t GRAPPA: a k-space implementation for dynamic MRI with high reduction factor. Magn Reson Med 2005;54:1172-84. [PubMed]
- Wiggins GC, Triantafyllou C, Potthast A, et al. 32-channel 3 Tesla receive-only phased-array head coil with soccer-ball element geometry. Magn Reson Med 2006;56:216-23. [PubMed]
- Wiggins GC, Polimeni JR, Potthast A, et al. 96-Channel receive-only head coil for 3 Tesla: design optimization and evaluation. Magn Reson Med 2009;62:754-62. [PubMed]
- Schmitt M, Potthast A, Sosnovik DE, et al. A 128-channel receive-only cardiac coil for highly accelerated cardiac MRI at 3 Tesla. Magn Reson Med 2008;59:1431-9. [PubMed]
- McDougall MP, Wright SM. 64-channel array coil for single echo acquisition magnetic resonance imaging. Magn Reson Med 2005;54:386-92. [PubMed]
- Blaimer M, Gutberlet M, Kellman P, et al. Virtual coil concept for improved parallel MRI employing conjugate symmetric signals. Magn Reson Med 2009;61:93-102. [PubMed]
- Sodickson DK, McKenzie CA. A generalized approach to parallel magnetic resonance imaging. Med Phys 2001;28:1629-43. [PubMed]
- Lin FH, Wald LL, Ahlfors SP, et al. Dynamic magnetic resonance inverse imaging of human brain function. Magn Reson Med 2006;56:787-802. [PubMed]
- Zhu Y, Hardy CJ, Sodickson DK, et al. Highly parallel volumetric imaging with a 32-element RF coil array. Magn Reson Med 2004;52:869-77. [PubMed]
- Grotz T, Zahneisen B, Ella A, et al. Fast functional brain imaging using constrained reconstruction based on regularization using arbitrary projections. Magn Reson Med 2009;62:394-405. [PubMed]
- Posse S, Otazo R, Tsai SY, et al. Single-shot magnetic resonance spectroscopic imaging with partial parallel imaging. Magn Reson Med 2009;61:541-7. [PubMed]
- Lin FH, Wang FN, Ahlfors SP, et al. Parallel MRI reconstruction using variance partitioning regularization. Magn Reson Med 2007;58:735-44. [PubMed]
- Tsai SY, Otazo R, Posse S, et al. Accelerated proton echo planar spectroscopic imaging (PEPSI) using GRAPPA with a 32-channel phased-array coil. Magn Reson Med 2008;59:989-98. [PubMed]
- Li Y, Huang F. Regionally optimized reconstruction for partially parallel imaging in MRI applications. IEEE Trans Med Imaging 2009;28:687-95. [PubMed]
- Li Y, Vijayakumar S, Huang F. Reconstruction in image space using basis functions for partially parallel imaging. Magn Reson Imaging 2008;26:461-73. [PubMed]
- Huang F, Li Y, Vijayakumar S, et al. High-pass GRAPPA: an image support reduction technique for improved partially parallel imaging. Magn Reson Med 2008;59:642-9. [PubMed]
- Samsonov AA. On optimality of parallel MRI reconstruction in k-space. Magn Reson Med 2008;59:156-64. [PubMed]
- Samsonov AA, Kholmovski EG, Parker DL, et al. POCSENSE: POCS-based reconstruction for sensitivity encoded magnetic resonance imaging. Magn Reson Med 2004;52:1397-406. [PubMed]
- Arunachalam A, Samsonov A, Block WF. Self-calibrated GRAPPA method for 2D and 3D radial data. Magn Reson Med 2007;57:931-8. [PubMed]
- Zhao T, Hu X. Iterative GRAPPA (iGRAPPA) for improved parallel imaging reconstruction. Magn Reson Med 2008;59:903-7. [PubMed]
- Ying L, Sheng J. Joint image reconstruction and sensitivity estimation in SENSE (JSENSE). Magn Reson Med 2007;57:1196-202. [PubMed]
- Madore B, Glover GH, Pelc NJ. Unaliasing by fourier-encoding the overlaps using the temporal dimension (UNFOLD), applied to cardiac imaging and fMRI. Magn Reson Med 1999;42:813-28. [PubMed]
- Brummer ME, Moratal-Pérez D, Hong CY, et al. Noquist: reduced field-of-view imaging by direct Fourier inversion. Magn Reson Med 2004;51:331-42. [PubMed]
- Griswold MA, Jakob PM, Nittka M, et al. Partially parallel imaging with localized sensitivities (PILS). Magn Reson Med 2000;44:602-9. [PubMed]
- Casper KA, Donnelly LF, Chen B, et al. Tuberous sclerosis complex: renal imaging findings. Radiology 2002;225:451-6. [PubMed]
- Punwani S, Taylor SA, Bainbridge A, et al. Pediatric and adolescent lymphoma: comparison of whole-body STIR half-Fourier RARE MR imaging with an enhanced PET/CT reference for initial staging. Radiology 2010;255:182-90. [PubMed]
- Hardie AD, Romano PB. The use of T2*-weighted multi-echo GRE imaging as a novel method to diagnose hepatocellular carcinoma compared with gadolinium-enhanced MRI: a feasibility study. Magn Reson Imaging 2010;28:281-5. [PubMed]
- Kellman P, Chefd’hotel C, Lorenz CH, et al. High spatial and temporal resolution cardiac cine MRI from retrospective reconstruction of data acquired in real time using motion correction and resorting. Magn Reson Med 2009;62:1557-64. [PubMed]
- Peters DC, Rohatgi P, Botnar RM, et al. Characterizing radial undersampling artifacts for cardiac applications. Magn Reson Med 2006;55:396-403. [PubMed]
- Smith ICP, Stewart LC. Magnetic resonance spectroscopy in medicine: clinical impact. Prog Nucl Magn Reson Spectrosc 2002;40:1-34.
- Law M. MR spectroscopy of brain tumors. Top Magn Reson Imaging 2004;15:291-313. [PubMed]
- Breuer FA, Kannengiesser SA, Blaimer M, et al. General formulation for quantitative G-factor calculation in GRAPPA reconstructions. Magn Reson Med 2009;62:739-46. [PubMed]
- Huo D, Wilson D, Griswold M, et al. Potential pitfalls of including reference data in parallel imaging reconstructions at high acceleration. Proc Intl Soc Mag Reson Med 2006;14:287.
- Wang Y. Description of parallel imaging in MRI using multiple coils. Magn Reson Med 2000;44:495-9. [PubMed]
- Haacke EM, Xu Y, Cheng YC, et al. Susceptibility weighted imaging (SWI). Magn Reson Med 2004;52:612-8. [PubMed]
- Fuderer M, van den Brink J, Jurrissen M. SENSE reconstruction using feed forward regularization. Proc Intl Soc Mag Reson Med 2004;11:2130.


