Efficient method to design RF pulses for parallel excitation MRI using gridding and conjugate gradient
Introduction
Spatially tailored radio frequency (TRF) pulses have been used in magnetic resonance imaging (MRI) to excite arbitrary spatial patterns. Parallel excitation (pTx) (1-3) techniques exploit the additional degree of freedom provided by the multiple transmit channels to shorten the radio frequency (RF) pulse duration and/or reduce the specific absorption rate (SAR) (4,5). The combination of TRF and pTx is recognized as a promising method to address several challenges in the high field MRI, such as field inhomogeneities and large SAR (6).
One widely used pulse design method under the small-tip-angle approximation is the spatial domain method (1). In this method, a specified target pattern and a k-space trajectory are specified and a set of linear system equations is built. The pulses can be designed by solving the linear equations using various numerical methods such as conjugate gradient (CG). One major problem of such a pulse design is the high computation cost since each iteration requires two matrix-vector multiplications. Generally, it can take up to 2-5 minutes (7) to design a long pulse, with full freedom in pulse magnitude and phase, which can prevent the pTx technique from being used in real-time applications. Meanwhile, the linear system matrix encountered in the design often requires memory allocations on the level of gigabyte.
Several existing methods have been reported to accelerate the spatial domain pulse design. For example, by employing the sparsity in the excitation pattern, the design equation can be transformed into the sparse domain and truncated to reduce the computation load (8,9). However, the efficiency of the method depends on the sparsity of the target pattern. Another method (10) accelerates the design of pTx pulses by using the graphic processing unit (GPU). However, the size of the pulses (proportional to pulse length and channel numbers) using GPU is limited by the available memory on GPU (no more than 2 GB for a single GPU). Meanwhile, rapid design methods based on conjugate gradient approach have been mentioned in (11). However, details of the design procedures were not provided.
In this paper, we present a detailed description of a fast pulse design method with Fourier domain gridding and a conjugate gradient method. In the method, the two computational expensive matrix-vector multiplications are substituted by two operators, which carry out the same physical functions as the multiplications. As a result, the computation and memory cost are significantly reduced. This method can be loosed regarded as the transmit version of (12), which deals with image reconstruction from data acquired using multi-channel receivers. Simulation results show that the proposed method was able to reduce the pulse design time and the memory cost by a factor of 8 and 103, respectively, all with the same excitation error and convergence rate
Theory and methods
Spatial tailored pulse design using the spatial domain method
We first briefly review the conventional spatial domain method (1) for spatial tailored pulse design with pTx. Under the small tip angle assumption (13), the excitation pattern of transverse magnetization and the complex RF pulse are Fourier pairs defined on the chosen k-space trajectory. pTx pattern of a multi-channel transmit system is the linear sum of the excitation patterns from all the channels weighted by the transmit sensitivity of each individual coil, i.e.,
[1] |
where is the specified spatial target pattern,
is the transmit sensitivity (i.e., B1+ map) of the l-th channel, and the excitation trajectory is defined as a reverse integral of the gradient
where T is the pulse duration. To solve the RF pulse bl(t), Eq. [1] is discretized both in time and in space to,
[2] |
which can be further written in matrix form
[3] |
where m is the vector form of the target pattern, Sl is the sensitivity matrix of the l-th channel (incorporating the constant ), A is the inverse Fourier encoding matrix defined on the k-space trajectory
, and bl is the sampled RF waveform vector of the l-th channel to be assigned.
The pulse design problem can then be formulated as a minimization problem,
[4] |
where the system matrix is defined as and the b vector is a stack of bl from all the channels. Due to the large system size, numerical methods such as CG method are often to solve the problem.
RF pulse design with gridding and conjugate gradient
In solving Eq. [4] with conjugate gradient method, significant portion of computations (more than 90%) are consumed by two matrix-vector multiplications with Afull and . Each of these two requires nmnsnc complex scalar multiplications, where nm, ns and nc are the number of pixels in the target pattern, the number of sampled points of the RF pulse for a single channel, and the number of transmit channels, respectively.
In the proposed method, two operators G1 and G2 are introduced to replace the matrix-vector multiplications without specifying the large system matrix. The operators combine the gridding of k-space data, fast fourier transform (FFT) and the sensitivity modulation, as shown in Figure 1. The operators are physically equivalent to the matrix-vector multiplications in the process of pulse design.
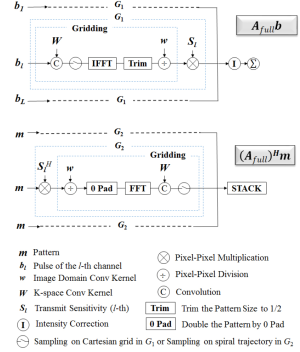
The forward operator G1 on bl[t] will perform the same function as the matrix-vector multiplication of the pulse of the l-th channel, i.e.,
[5] |
The A matrix represents an inverse Fourier operator that maps bl[t] from the non-Cartesian excitation trajectory (e.g., spiral trajectory) to a spatial domain pattern on the Cartesian grid. Thus, it can be replaced by Fourier domain gridding, as shown in (7), followed by an inverse FFT. In the process of the gridding, the pulse (k-space data) bl[t] is first convolved with the Kaiser-Bessel kernel and then sampled on the Cartesian grid with doubled resolution corresponding to 2× FOX (field of exciation). The reason of sampling on a grid with finer resolution is to reduce the aliasing artifact caused by the convolution kernel in spatial domain. Then, an inverse FFT of the Cartesian data generates a spatial pattern of size 2× FOX. Subsequently, the pattern is trimmed from the center to size of FOX and divided pixel-by-pixel by the inverse Fourier transform of the convolution kernel to compensate the convolution. After gridding, the pattern is multiplied by the transmit sensitivity
in a voxel-by-voxel fashion, and then reshaped into the vector form. Then, according to Eq. [5], the final pattern is achieved by linearly adding the patterns from all channels,
[6] |
Similarly, the backward operator G2 performed on the spatial pattern plays the same role as the Hermitian transposed matrix-vector multiplication for the l-th channel,
[7] |
Specifically, in this backward operator, the spatial pattern is first modulated by the Hermitian transposed transmit sensitivity of the l-th channel as . Then, the Fourier encoding matrix AH, which maps the spatial domain Cartesian pattern to data on the non-Cartesian k-space trajectory
, is substituted by a gridding process. In this gridding process, the sensitivity-modulated pattern
is first divided pixel-by-pixel by the inverse Fourier transform of the convolution kernel and zero-padded to the size of 2× FOX. The k-space data on the Cartesian grid is then obtained by the FFT of the spatial pattern. Finally, the k-space data is convolved with the convolution kernel and sampled along the desired k-space trajectory
.
The result of the Hermitian transpose multiplication of the system matrix is a stack of vectors from individual channel results obtained from Eq. [7] as,
[8] |
With these two operators, the same CG method as in the conventional method can be used to solve the pulse design problem with much higher efficiency, because the two multiplications required during each CG iteration are now be replaced by the operators.
In this paper, the gridding part in operator G1 is implemented using an online toolbox (14). And the gridding part in operator G2 is implemented with a 2D interpolation function in Matlab. Proper modifications including phase correction, zero-padding, and intensity correction are made in both operators.
The approximate computation cost (number of complex scalar multiplications) of the operator G1 and the direct matrix multiplication are compared in Table 1. Parameter ε=2 denotes the factor of oversampling/zero-padding and w=6 is the size of convolution kernel. Therefore, the computation cost is approximately reduced by the factor of with the proposed method. For example, for a pulse with ns=1,024 time points, a target pattern defined on a grid with nm=1,024 spatial points, and nc=8 transmit channels, the operator G1 would reduce the computation cost by a factor of about 12. The computation of
gains similar computational efficiency.

Full table
The savings in memory cost is even more significant. In the proposed method, only several matrices of size nmnc need to be saved. In the direction matrix multiplication, the system matrix Afull with nmnsnc elements needs to be stored. In the above example, the memory cost in the proposed method is about ~1,000 times less than that in a conventional method.
Computer simulations
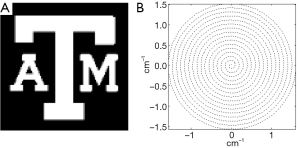
To evaluate the performance of the proposed design method, a 2-D tailored pulse will be designed to excite a 2-D pattern, which is shown in Figure 2A over a 20×20 cm2 FOX. An 8-ch linear transmit array and a spiral trajectory (shown in Figure 2B) with 2× pTx acceleration are used in the design, with both the proposed method and the conventional spatial domain method. Transmit sensitivity is simulated using a quasi-static method. The total pulse length is 5.3 msec with a dwell time of 0.0026 msec. The same setups, including parameters, transmit sensitivities and the target pattern, are used in both simulations.
To show the convergence of the design, the residual of each CG iteration is measured by the L2 norm of the current residual vector. The quantitative difference between the two methods in term of designed pulse, excitation error, design time and memory cost are compared. The excitation patterns for excitation error measurement are obtained from a Bloch simulator.
In addition, the stability of the proposed method is tested under inaccurate transmit B1 sensitivity is investigated and compared with that of the conventional method. The pulses are designed with the corrupted B1+ sensitivities with different SNR using the conventional method and the proposed method. A pTx acceleration of 2 is used in all designs. The spiral-in trajectory and transmit sensitivity are the same as that in previous experiments. The excitation patterns are obtained using the Bloch simulator with the true B1+ sensitivity without noise. In each case, complex Gaussian noise is added to the “true” transmit sensitivities. The SNR of the transmit B1 sensitivity is defined as SNR =10log10(Ps/Pn), where Ps is the average power of true B1+ sensitivity of all the channels and Pn is the power of the added Gaussian noise.
All simulations are performed in Matlab 2011b (Math Works, Natick, MA) on a desktop with 2.67 GHz i-7 CPU and 9 GB memory.
Results
The results of the computer simulations of 2D pTx pulse design are shown in Figure 3. Convergence behavior of the proposed method is shown in the residuals curve in Figure 3A. Its difference to that of the conventional design is shown in Figure 3B. As can be seen, the CG in the proposed method converges towards zero at the same rate as the conventional method and the relative difference is within 0.5%. This shows that the gridding introduced error is mall during each iteration.
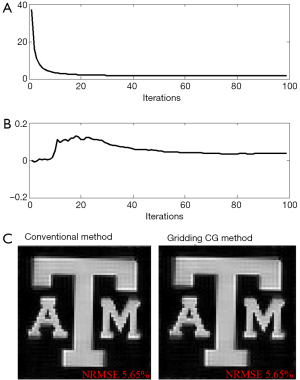
The excited patterns for the two methods are compared in Figure 3C. Both methods led to a normalized root mean square error of 5.65% in this case. This is expected because the maximum error of a single gridding step is controlled below 0.5%. Thus, the proposed method can achieve the same accuracy as the conventional method. Note that the proposed method took only 2.3 seconds to complete the iterations, while the conventional design method took 18 seconds. Therefore the design efficiency is improved by a factor of eight in this example. In addition, the system matrix Afull requires 1,012 MB memory to save in the conventional method. In the proposed method, less more than 5 MB memory is required in total.
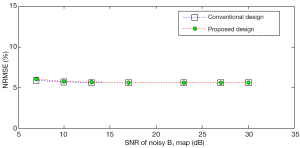
Figure 4 shows excitation errors of the pulses designed using the conventional method and the proposed method under different perturbations. As the SNR of the B1+ sensitivities increases, the error decreases for both the methods. The error curves of these two methods are almost the same. Thus, the proposed method has the same stability to inaccurate B1+ measurement as the conventional method.
Conclusions
In this work, we proposed an efficient method to RF pulses in pTx. The method uses data gridding and conjugate gradient optimization. By replacing the computationally expensive matrix operations with gridding-based operations, the design speed can be significantly improved. Computer simulations show that an order of magnitude computational efficiency is feasible without compromising the design accuracy. In addition, the proposed method reduced memory cost by >103 times in the simulated studies. This eases the memory burden of designing longer pTx pulses with more transmit channels or patterns defined on finer resolution. Furthermore, this enables implementing the pulse designs on GPU for further speed-ups. The proposed method can be applied to accelerate other spatial domain pTx pulse designs, for example, with regularization terms to control the SAR.
Acknowledgements
This work was supported in part by the NSF (National Science Foundation) under award number 0748180. Any opinions, findings and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect those of the NSF.
Disclosure: The authors declare no conflict of interest.
References
- Grissom W, Yip CY, Zhang Z, et al. Spatial domain method for the design of RF pulses in multicoil parallel excitation. Magn Reson Med 2006;56:620-9. [PubMed]
- Katscher U, Börnert P, Leussler C, et al. Transmit SENSE. Magn Reson Med 2003;49:144-50. [PubMed]
- Zhu Y. Parallel excitation with an array of transmit coils. Magn Reson Med 2004;51:775-84. [PubMed]
- Graesslin I, Homann H, Biederer S, et al. A specific absorption rate prediction concept for parallel transmission MR. Magn Reson Med 2012;68:1664-74. [PubMed]
- Collins CM, Li S, Smith MB. SAR and B1 field distributions in a heterogeneous human head model within a birdcage coil. Specific energy absorption rate. Magn Reson Med 1998;40:847-56. [PubMed]
- Bandettini PA, Bowtell R, Jezzard P, et al. Ultrahigh field systems and applications at 7 T and beyond: progress, pitfalls, and potential. Magn Reson Med 2012;67:317-21. [PubMed]
- Setsompop K, Wald LL, Alagappan V, et al. Parallel RF transmission with eight channels at 3 Tesla. Magn Reson Med 2006;56:1163-71. [PubMed]
- Feng S, Ji J. A novel fast algorithm for parallel excitation: pulse design in MRI. Conf Proc IEEE Eng Med Biol Soc 2012;2012:1102-5.
- Feng S, Ji JX. An Algorithm for Fast Parallel Excitation Pulse Design. In: Proceedings of the 21th Annual Meeting of ISMRM; Salt Lake City, UT, USA 2013. Available online: http://ismrm.org/13/
- Deng W, Yang C, Stenger VA. Accelerated multidimensional radiofrequency pulse design for parallel transmission using concurrent computation on multiple graphics processing units. Magn Reson Med 2011;65:363-9. [PubMed]
- Yip CY, Fessler JA, Noll DC. Advanced three-dimensional tailored RF pulse for signal recovery in T2*-weighted functional magnetic resonance imaging. Magn Reson Med 2006;56:1050-9. [PubMed]
- Pruessmann KP, Weiger M, Börnert P, et al. Advances in sensitivity encoding with arbitrary k-space trajectories. Magn Reson Med 2001;46:638-51. [PubMed]
- Pauly J, Nishimura D, Macovski A. A k-space analysis of small-tip-angle excitation. Journal of Magnetic Resonance 1969;1989:43-56.
- Ferrara M. NUFFT, NFFT, USFFT. Available online: http://www.mathworks.com/matlabcentral/fileexchange/25135-nufft--nfft--usfft


