Eight channel transmit array volume coil using on-coil radiofrequency current sources
Introduction
A major confounding factor for the development of MRI applications at ultra-high B0 field strength is radio frequency (RF) field inhomogeneity (1-4). Typical RF volume coils consist of several sources of B1 field and generate a uniform resultant B1 field by constructive superposition of the individual B1 fields in the volume of interest (5,6). RF energy is transferred through one or two ports to the RF coil, which is designed to ensure sinusoidal distribution of currents in the circumferential direction. At high Larmor frequency, the short wavelength of the B1 field in high dielectric media, combined with multiple sources, causes significant inhomogeneity in the total B1 field due to alternate regions of constructive and destructive interference. In addition, the enhanced coil-sample interaction leads to B1 field inhomogeneity caused by perturbation of the sinusoidal current distribution due to either non-uniform loading or mode mixing or both (7,8).
Studies have shown that B1 field shimming, implemented by adjusting the amplitude and phase of B1 field from each individual transmitter may dramatically improve B1 field homogeneity (9,10). Parallel transmission techniques that utilize two or more degrees of freedom are typically used for B1 field shimming. Parallel transmission relies on the ability to drive separate coil elements with independent waveforms, amplitudes, and phases and requires the transmitting elements to be well decoupled from each other. Traditional RF volume coils, such as birdcage coils and transverse electromagnetic (TEM) coils, are multi-modal resonant structures. The transmitting elements of such structures are strongly coupled to each other, making independent control extremely difficult to achieve. The transmitting elements may be decoupled from one another using coil overlapping to achieve good decoupling between nearest neighbors (11), while distant neighbors may be decoupled using capacitive networks (12). This is a complicated arrangement that is difficult to design and is sensitive to changes in coil loading. Microstrip transmitting elements (13) have gained in popularity as parallel transmitting elements due to their favorable decoupling characteristics. However, microstrip transmitters require dedicated high power RF amplifiers because good decoupling is achieved at the cost of transmitting efficiency. This drives up the per-channel cost of the transmit chain, making the parallel transmission system expensive. The Cartesian feedback technique introduced by Hoult et al.(14), relies on subtraction of scaled coupled voltages from the input to the amplifier. The advantage of this technique is that it enables the use of transmitting elements of arbitrary geometry with little effect on the decoupling performance, thereby potentially increasing the transmit efficiency. This technique and isolation amplifier technique introduced by Chu et al. (15) are effective, but involve the use of sophisticated feedback circuits and output matching networks (16).
RF current source drives for series tuned transmitting elements seems to be a promising alternative technique to the above. The concept, originally introduced in (17) and followed by a number of variants (18,19) is an open loop technique that involves the use of the transmitting element as the output circuit of the RF power amplifier, where the active device is used as a controlled current source. The advantage of this design is that decoupling between neighboring transmitting elements is provided by the high internal impedance of the current source, enabling the optimization of the transmitting element for transmit efficiency.
In this paper, we present a novel transmit array design based on RF current source excitation (17) that enables B1 field shimming. We describe the design and construction of an 8-channel transmit coil with coil-mounted RF current sources and demonstrate deterministic B1 field pattern control through independent control of the amplitude and phase in each transmitting element.
Methods
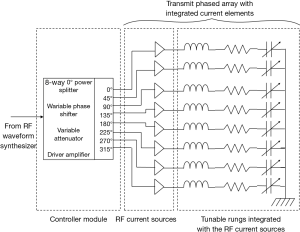
A block diagram of the transmit coil system is shown in Figure 1. The transmit coil system consists of an 8-channel controller module and eight current elements, arranged on a cylindrical former to form a transmit phased array volume coil. A current element consists of a series tuned transmitting element that forms the output circuit of a controlled RF current source.
8-channel controller module
An 8-eight channel controller module (Figure 2) was constructed to provide drive voltage to the corresponding RF current source with independent amplitude and phase control. The module consisted of a single RF input that was split into eight channels using an 8-way, 0° power splitter (ZFSC-8-1, Mini-Circuits). Using coaxial delay lines, fixed phase shifts were implemented such that each channel was progressively lagging 45o with respect to the previous channel. Each controller channel consisted of a DC voltage controlled attenuator (3-55 dB attenuation, 0-17V DC, RVA2500, Mini-Circuits), a DC voltage controlled phased shifter (180° linear phase shift, 0-12V DC, JSPHS-150, Mini-Circuits) and 2 stages of driver amplifiers [ERA-5SM (18 dBm output power) and HELA 10D (30 dBm output power), Mini-Circuits]. A bank of potentiometers provided the control voltages for the attenuators and phase shifters.

8-channel transmit coil
A cylindrical acrylic former (OD: 305 mm, ID: 292 mm, length: 305 mm) was used as the base structural material for the transmit array coil design. Eight rectangular acrylic strips, 279 mm long and 19 mm wide were glued to the inner surface of the former at equal azimuthal angles, 45o apart. Strips of copper tape 6 mm wide and 254 mm long were glued to the long edge of the rectangular strips, facing into the cylindrical cavity and formed the transmitting elements of the RF transmit coil.
An RF shield consisting of capacitively coupled strips of copper to minimize the formation of gradient induced eddy currents was tightly wrapped around the outer circumference of the cylindrical former. The PC boards containing the RF current source circuitry (17) were mounted on top of the RF shield. At one end, the transmitting elements were connected to the outputs of the RF current sources with strips of copper tape that were passed through the holes drilled into the former and RF shield. Each transmitting element was capacitively divided into five segments with 47 pF chip capacitors (ATC corp.). At the other end, each transmitting element was connected to a copper strip cut out on the RF shield. This copper strip was, in turn, connected to the RF shield via a trimmer capacitor, which was used to series tune the coil at 127.72 MHz. Figure 3 shows a picture of the completed coil.

The RF current source boards were divided into two groups of four boards each. The drain supply traces on boards of each group were connected in parallel using 14 AWG insulated copper wire. The two groups were in turn connected in parallel to an external high current, fixed voltage DC power supply (28 V, 12 A, Astron corp.) through heavy duty RF chokes. The gate supply traces on all eight boards were connected in parallel. In order to minimize heat dissipation from the MOSFET’s, the gate bias was provided to them only during the RF transmit pulse. The gate DC supply was derived from the ‘active low’ unblanking signal of the GE 3T transmitter, which is used to enable the system RF power amplifier during the transmit event. An op-amp inverter was implemented to invert the unblanking signal such that the MOSFET gate on each channel was provided with a DC bias of 3.6 V during RF transmit. The MOSFETs were thus biased to class AB linear operation during RF transmission and were turned OFF at all other times.
Integration with MRI scanner
The transmit coil was integrated with the GE Eclipse 3T scanner. The RF power input to the controller module was derived from the head coil port of the MRI scanner. The RF power was attenuated such that the maximum power input to the controller module did not exceed 15 dBm at the maximum transmit gain setting allowed by the system. The eight outputs of the controller module were connected to the inputs of the eight RF current sources mounted on the transmit coil.
Receive coil
An actively detuned quadrature saddle receive-only volume coil was constructed on an acrylic former (OD: 203 mm, ID: 191 mm, length: 254 mm) for imaging experiments (20). The coil was placed coaxially in the cavity of the transmit coil as shown in Figure 4. The quadrature coil outputs were connected to 2 channels of the 8-channel system receiver via a custom-built system interface. Active detuning of the receive coil during the transmit cycle was achieved using four PIN diode decoupling networks, two for each saddle pair. The PIN diode bias for the active decoupling networks was drawn from system PIN diode bias drivers.

Imaging experiments
The goal of imaging experiments was to demonstrate B1 field pattern control by recreating the characteristic modal patterns of linear and quadrature driven TEM resonators, using the 8-channel transmit array. A homogeneous cylindrical phantom filled with silicone oil was used for this purpose. A low flip angle Gradient Echo (GE) pulse sequence (TE/TR =20/800 ms, α=20°) was used to obtain images that approximated transmit field maps.
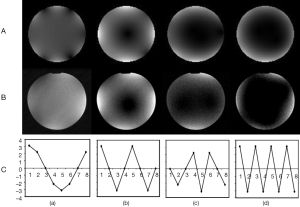
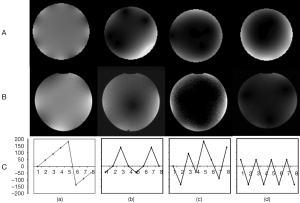
The current amplitudes and phases on the current elements were set using the controller module. For linear TEM resonator mode patterns, the relative phase between the current elements was set to zero and only the current amplitudes were dialed in as shown in Figure 5 (row C). For the quadrature TEM resonator mode patterns, the current amplitudes were set to a fixed value and relative phase between successive current elements was set to 45° (Figure 6, row C) for a cumulative phase of 360°. All the images obtained were compared to simulated field patterns of TEM resonator modes. Finally, the phase progression on the transmit array was reversed to obtain an anti-quadrature image in order to test the quality of circular polarization.
Simulations
The characteristic modal patterns of a TEM resonator were simulated for both 1-port linear excitation and 2-port quadrature excitation. For 1-port linear excitation, each modal pattern was obtained by exciting the resonator at the characteristic modal resonance frequency. For 2-port quadrature excitation, two geometrically orthogonal ports of the TEM resonator model were excited in phase quadrature. In both cases, the TEM resonator model was tuned to the appropriate mode of interest.
Results
The simulated field patterns of the degenerate modes of an 8-rung TEM resonator, excited at a single port, are shown in row (A) of Figure 5. These modal field patterns are generated at characteristic modal resonant frequencies due to current amplitude distributions as shown in the corresponding charts in row (C). For single port excitation, the relative phase between the rung currents is zero. Images obtained by setting up similar current amplitude distributions on the current elements that make up the transmit array show field patterns that are in close agreement with the simulated results. It should be noted however, that with the transmit array, the modal patterns are generated at a single frequency, the Larmor frequency, by independently controlling the current amplitudes on the current elements.
The simulated field patterns of the degenerate modes of a quadrature excited 8-rung TEM coil are shown in row (A) of Figure 6. In this case, the modal field patterns are generated at characteristic modal resonant frequencies due to the phase distribution of currents on the rungs as given by the charts shown in row (C). In theory, the vector sum of resonator currents due to the 2-port quadrature excitation should result in constant current amplitude for the uniform mode. The distribution of current amplitudes for higher order modes is more complex. Comparison of the real [row (B)] and simulated images shows that there is a good correspondence between modes 1 and 5 whereas modes 3 and 7 do not correspond. This could be explained by the fact that excitation ports are orthogonal to each other for modes 1 and 5 and hence the fields do not interfere with each other. However, for modes 3 and 7, the excitation ports are not orthogonal and hence there is cross-talk as shown by the simulations. In the case of the transmit coil, however, the current distributions were determined on the assumption of orthogonality of the excitation ports for all modes. Therefore, these images are closer to the linear excitation case.
Phantom images obtained by setting up quadrature and anti-quadrature phase progression of currents on the transmit array current elements are shown in Figure 7. Both images are set to the same window and level values. The anti-quadrature image exhibits very low signal compared to the quadrature in many regions with complete elimination of signal in some regions. With finer adjustments of the relative phase, it may be possible to achieve high quality circular polarization.
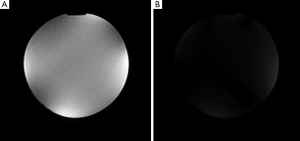
The bright spots seen at the edges of the images are due to the fact that the phantom almost completely filled the cavity of the receive coil. Since the magnetic flux density is the highest near a current carrying conductor, the B1 field patterns show bright spots in these regions. In the case of the anti-quadrature image, residual coupling between the receive and transmit coils may cause degradation in the circular polarization.
Discussion
The mode patterns of a birdcage or TEM coil occur at distinct frequencies as determined by the mutual inductances between their resonant loops. This is characteristic of a periodic, resonant structure. The resonant modes of a resonant structure are a potential liability at high field strengths. Load-coil interactions at high field strengths cause significant shift in the resonant frequency of the loops of a resonant coil. With asymmetric loading, the resonant frequencies of the heavily loaded loops may shift more than those of the lightly loaded loops, thereby exciting higher order modes in some loops. This causes field inhomogeneity due to mode mixing (7).
In contrast, the mode patterns of the non-resonant transmit array of current elements are generated at a single frequency, the Larmor frequency, by adjusting the amplitudes and phases of the currents on the current elements. This ability of the transmit array to generate controlled B1 patterns could potentially be a useful tool to optimize homogeneity in the presence of lossy dielectric loads. For instance, it is known that images of samples with high dielectric constants have a bright central spot with alternating dark and bright bands around it (1,2,4,9,10,21). This is a typical interference pattern. In such cases, it may be advantageous to generate a mode 2 or mode 3 pattern or even a combination of modal patterns which would be possible with a current element array.
Resonant coils such as the birdcage and TEM coils are highly efficient as they exhibit high current gain. This is the nature of a resonant structure. The main disadvantage of the transmit array design is its low efficiency. The amplitude of the current driven through the rung is entirely dependent on the MOSFET drive voltage and the current handling capacity of the MOSFET. Therefore, the large current requirements of bigger volume coils would necessitate the use of MOSFET’s with very high current handling capacity and innovative heat dissipation designs. The primary advantage of the RF current source driven transmit array is its ability to generate controlled B1 field patterns by independently controlling the current amplitude and phase on the component current elements. This feature may be used to perform B1 field shimming in a simple and predictable manner.
Conclusions
The design and development of a novel 8-channel transmit phased array coil with dedicated RF current source drive per transmit channel has been described in detail. The volume coil has a non-resonant structure due to the weak coupling between the current elements, thereby enabling independent control of current amplitude and phase on each current element. B1 field pattern control has been demonstrated by setting up desired currents on the current elements using the controller module. The coil design enables B1 field shimming in a simple and predictable manner.
Acknowledgements
The authors gratefully acknowledge the support from the National Science Foundation (BES0101059). The authors would also like to thank Mr. John Lorbiecki for building the acrylic former and Dr. Dave Brown and Mr. LeRoy Blawat for stimulating conversations on RF circuit design.
Disclosure: The authors declare no conflict of interest.
References
- Alecci M, Collins CM, Smith MB, et al. Radio frequency magnetic field mapping of a 3 Tesla birdcage coil: experimental and theoretical dependence on sample properties. Magn Reson Med 2001;46:379-85. [PubMed]
- Chen J, Feng Z, Jin JM. Numerical simulation of SAR and B1-field inhomogeneity of shielded RF coils loaded with the human head. IEEE Trans Biomed Eng 1998;45:650-9. [PubMed]
- Jin J, Shen G, Perkins T. On the field inhomogeneity of a birdcage coil. Magn Reson Med 1994;32:418-22. [PubMed]
- Yang QX, Wang J, Zhang X, et al. Analysis of wave behavior in lossy dielectric samples at high field. Magn Reson Med 2002;47:982-9. [PubMed]
- Hayes CE, Edelstein WA, Schenck JF, et al. An efficient, highly homogeneous radiofrequency coil for whole-body NMR imaging at 1.5 T. J Magn Reson 1969;63:622-8.
- Vaughan JT, Adriany G, Garwood M, et al. Detunable transverse electromagnetic (TEM) volume coil for high-field NMR. Magn Reson Med 2002;47:990-1000. [PubMed]
- Tropp J. A model for image shading in multi-mode resonators. In Proceedings of the 9th annual meeting ISMRM, 2001:1129.
- Ibrahim TS, Lee R, Baertlein BA, et al. Computational analysis of the high pass birdcage resonator: finite difference time domain simulations for high-field MRI. Magn Reson Imaging 2000;18:835-43. [PubMed]
- Ibrahim TS, Lee R, Abduljalil AM, et al. Dielectric resonances and B(1) field inhomogeneity in UHFMRI: computational analysis and experimental findings. Magn Reson Imaging 2001;19:219-26. [PubMed]
- Vaughan JT, Garwood M, Collins CM, et al. 7T vs. 4T: RF power, homogeneity, and signal-to-noise comparison in head images. Magn Reson Med 2001;46:24-30. [PubMed]
- Zhu Y. Parallel excitation with an array of transmit coils. Magn Reson Med 2004;51:775-84. [PubMed]
- Jevtic J. Ladder networks for capacitive decoupling in phased-array coils. In Proceedings of the 9th Annual Meeting of ISMRM, Glasgow, Scotland, 2001.
- Adriany G, Van de Moortele PF, Wiesinger F, et al. Transmit and receive transmission line arrays for 7 Tesla parallel imaging. Magn Reson Med 2005;53:434-45. [PubMed]
- Hoult DI, Kolansky G, Kripiakevich D, et al. The NMR multi-transmit phased array: a Cartesian feedback approach. J Magn Reson 2004;171:64-70. [PubMed]
- Chu X, Yang X, Liu Y, et al. Ultra-low output impedance RF power amplifier for parallel excitation. Magn Reson Med 2009;61:952-61. [PubMed]
- Hollingsworth N, Moody K, Nielsen JF, et al. Tuning ultra-low output impedance amplifiers for optimal power and decoupling in parallel transmit MRI. In Biomedical Imaging (ISBI), 2013 IEEE 10th International Symposium on, 2013:946-9.
- Kurpad KN, Wright SM, Boskamp EB. RF current element design for independent control of current amplitude and phase in transmit phased arrays. Concepts in Magnetic Resonance Part B 2006;29:75-83.
- Gudino N, Heilman JA, Riffe MJ, et al. On-coil multiple channel transmit system based on class-D amplification and pre-amplification with current amplitude feedback. Magn Reson Med 2013;70:276-89. [PubMed]
- Lee W, Boskamp E, Grist T, et al. Radiofrequency current source (RFCS) drive and decoupling technique for parallel transmit arrays using a high-power metal oxide semiconductor field-effect transistor (MOSFET). Magn Reson Med 2009;62:218-28. [PubMed]
- Ginsberg DM, Melchner MJ. Optimum Geometry of Saddle Shaped Coils for Generating a Uniform Magnetic Field. Rev Sci Instrum 2003;41:122-3.
- Bottomley PA, Andrew ER. RF magnetic field penetration, phase shift and power dissipation in biological tissue: implications for NMR imaging. Phys Med Biol 1978;23:630-43. [PubMed]


