
Volumetric cine magnetic resonance imaging (VC-MRI) using motion modeling, free-form deformation and multi-slice undersampled 2D cine MRI reconstructed with spatio-temporal low-rank decomposition
Introduction
Target localization is critical for stereotactic body radiation therapy (SBRT) due to high fractional dose, tight planning target volume (PTV) margin, and long treatment time. Localization is especially critical for liver and lung treatment since respiratory motion can affect target location (1,2). Reducing target localization errors helps to make the radiotherapy more effective based on previous studies, which showed that minimizing treatment errors was correlated with reduced normal tissue toxicity and improved tumor control (3,4). Developing real-time volumetric imaging is necessary for improving on-board target localization.
Recently, on-board magnetic resonance imaging (MRI) has been introduced in clinics for target localization due to no ionizing radiation dose and superb soft tissue contrast. 2D cine MRI and 4D MRI techniques have been developed recently for imaging moving targets (5-10). 2D cine MRI can track the in-plane motion of the target in 2 dimensions by generating 2D images in the specific plane of the patient continuously. 2D cine MRI does not have volumetric information, and thus can only track the tumor in two dimensions and cannot capture the out of plane motion or the 3D deformation of the target. Orthogonal 2D MRI can be acquired to track out of plane motion, but there are no clinically available techniques that allow for simultaneous orthogonal 2D cine MRI acquisition for 3D verification or tracking (11,12). In addition, acquiring orthogonal 2D cine MRI would not provide 3D information of the target, which is important for verifying/tracking the target deformation during treatment and post treatment evaluation of the accumulated dose delivered to the target.
A volumetric-cine MRI (VC-MRI) method was developed using a single 2D cine on-board MRI slice along with prior 4D MRI to estimate on-board 3D cine MRI for target localization (13). The method was accelerated using undersampled single 2D cine images to improve the temporal resolution of the VC-MRI (14). The original method used a motion model (MM) to estimate a deformation field map (DFM) used to estimate the VC-MRI. The limitation to this method is that the VC-MRI accuracy is limited when there are large anatomical changes, such as tumor size change from simulation to treatment, due to the limitations of the MM.
This study aims to do the following: (I) introduce a free-form deformation (FD) model to correct for any errors in the MM; (II) acquire multiple undersampled 2D cine images to provide adequate information for FD estimation while maintaining or improving the temporal resolution of the VC-MRI; (III) to evaluate the effect of 2D cine slice orientation, slice location and slice number on the VC-MRI estimation accuracy. The undersampled cine images are reconstructed based on low-rank decomposition in the spatial-temporal domain (6). The new method proposes to further improve the accuracy and temporal resolution of VC-MRI for different patient scenarios, making it a robust real-time 3D MRI technique. The method is evaluated using an anthropomorphic digital XCAT phantom. The novel undersampling technique is evaluated using four liver patients’ data.
Methods
The overall workflow is shown in Figure 1. The on-board VC-MRI at any time step is assumed to be a deformation of MRIprior, or the end-of-expiration (EOE) phase of a 4D MRI taken during simulation, and the goal is to solve for the DFM that best estimates the on-board VC-MRI, by using on-board undersampled 2D cine MRIs reconstructed using a low-rank k-t SLR reconstruction method. Principal component analysis (PCA) is used on DFMs obtained from the phases of the 4D MRI to extract out three deformation modes. The deformation modes are optimized in a MM method to obtain a coarse estimation of the DFMs. Then, the DFM is fine-tuned using a FD method, which lets each voxel in the DFM deform freely, without assuming any prior motion. More detail on the overall methods is described in the next sections.
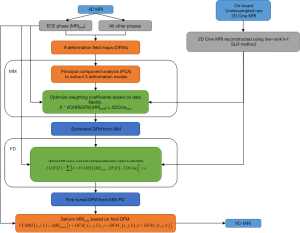
MM
Based on the previously developed method, the VC-MRI is estimated as follows (13,14). Prior 4D MRI is taken during simulation, and the EOE phase is designated as MRIprior. The on-board VC-MRI at each respiratory phase is considered a deformation of MRIprior, shown in Equation [1]. The goal is to solve for the DFM that best estimates the on-board VC-MRI.
|
| [1] |
DFMx, DFMy and DFMz represent the deformation fields along the three canonical directions of the Cartesian coordinate system. The DFMs are solved based on a MM optimization method by deforming MRIprior to all other phases of the 4D MRI. PCA is used to extract out three major deformation modes from the DFMs. Then, the DFM can be represented as a weighted linear combination of the first three major deformation modes, as shown by Equation [2].
|
| [2] |
DFM0,ave is the average of the original DFMs from the prior 4D MRI, wj are the weighting coefficients,
|
| [3] |
Here, S is the operator to extract the corresponding slice of the VCMRI as the 2DCine slices. The data fidelity constraint matches the on-board 2D cine MRI to the corresponding slice of the VC-MRI. After the weighting coefficients are solved for, the final DFM is calculated and VC-MRI can be generated by using Equation [1]. For more details about the original VC-MRI method, refer to previous publications (13,14).
FD
Anatomical changes from simulation to treatment, such as tumor size changes, may affect the accuracy of the DFM due to an inaccurate MM. To solve these potential issues, a FD method is applied afterwards to fine tune the DFM. The DFM solved for by the MM is used as the initial starting point of the DFM for the FD. Without assuming any MMs, the FD method allows each voxel in the DFM to move freely, while minimizing deformation energy to preserve the smoothness of the DFM. The energy of the DFM is defined in Equation [4] (15,16).
|
| [4] |
The goal of the FD optimization is to find the DFM satisfying Equation [5], subject to the data fidelity constraint in Equation [6], which aims to minimize the sum of the differences between each of the on-board 2D cine images with the corresponding slices of the VC-MRI.
|
| [5] |
|
| [6] |
Here, i represents the sum over the multiple cine slices. The energy constraint and the data fidelity constraint work in opposition. Because of that, they are enforced consecutively through gradient descent optimization to adaptively control the step size to reach final convergence (15).
Multi-slice undersampled 2D cine MRI
FD estimation requires the use of multiple on-board 2D images in the data fidelity constraint due to its large number of variables. Using undersampled 2D cine MRI allows for acceleration to acquire multiple 2D cine MRI for VC-MRI estimation without sacrificing its temporal resolution. A previously developed low-rank decomposition method was used to reconstruct the undersampled cine images (6,17). The low-rank decomposition method uses k-t SLR to reconstruct highly undersampled 2D cine images, utilizing both spatial and temporal information (6,17). The spatio-temporal signal to solve for can be denoted as γ(s,t), where s is the spatial location and t is the time. Then, γ(s,t) can be rearranged into a matrix, x, shown in Equation [7] (17).
|
| [7] |
Where the rows of x correspond to the voxels and the columns correspond to the temporal samples.
The main optimization equation used to reconstruct the undersampled k-space data is shown in Equation [8].
|
| [8] |
The images are assumed rank deficient, and so the sparse vector x can be generalized to a low-rank matrix, X. Fp is the partial Fourier transformation, k is the undersampled k-space data, and λ1 and λ2 are regularization parameters. A total variation (TV) constraint in both the spatial and temporal domain was used to utilize the sparse gradients of the dynamic images. Equation [8] is named as k-t SLR. Additional details of the reconstruction algorithm can be found in previous publications (6,17). The k-t SLR produces high quality reconstructed images based on highly undersampled k-space data due to the decomposition in the spatial-temporal domain by utilizing the anatomical consistency from the temporal images.
XCAT simulation
A digital anthropomorphic phantom, XCAT, was used to simulate the prior 4D MRI and ground-truth on-board VC-MRI (18). The respiratory motion for the body of the phantom and the tumor of the phantom were controlled by two respiratory curves, separately: the diaphragm curve [superior-inferior (SI) motion] and the chest wall curve [anterior-posterior (AP) motion]. No lateral motion was simulated.
Prior 4D MRI simulation
A spherical lesion of 30 mm diameter was simulated in the middle of the lung in XCAT. The respiratory cycle was set to 5 second, and the amplitudes of the diaphragm curve and chest wall curve were set to 3 and 2 cm, respectively. A ten-phase 4D MRI was simulated as the prior 4D MRI. The MRI volume of each phase was composed of 256×256×100 voxels, with each voxel measuring 1.875×1.875×3 mm3 in dimension. The XCAT phantom was generated in activity mode in order to produce MRI-like images.
Ground-truth VC-MRI simulation
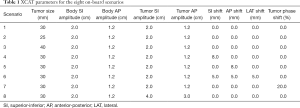
Based on parameters used to generate the prior 4D MRI, eight patient scenarios were simulated for on-board volume sets to reflect different on-board respiratory and anatomical changes. The body volume and the tumor volume get generated separately, each with their own corresponding diaphragm curve (SI motion) and chest wall curve (AP motion). Various SI and AP amplitudes were chosen for the body and tumor volumes separately. Different shifts were also simulated in the SI, AP and lateral directions, in which case the tumor volume is shifted in the corresponding direction relative to the prior 4D MRI simulation. Table 1 shows the parameters for the eight scenarios.
Full table
On-board 2D cine MRI simulation
2D sagittal, axial and coronal slices were extracted from the ground-truth on-board VC-MRI at various locations through and around the tumor in the MRIprior volumes to simulate on-board 2D cine MRI. The direct Fourier transform of each slice was taken to simulate fully sampled k-space. Then, the k-space data was undersampled and reconstructed based on k-t SLR described in section “FD”. The image size was 256×256 with 21 time-steps. Each cine slice had an image resolution was 1.875×1.875 mm2. Fully sampled k-space data was defined as sampling 256 phase-encoded lines. In this study, 10% of fully sampled k-space data was acquired on a Cartesian coordinate system. Of the 10% of the undersampled data, 10% of that was acquired uniformly in the center k-space. The rest of k-space was randomly sampled. Each of the 21 time-step slices had different random phase-encoded lines sampled.
Effect of region of interest (ROI) selection
In the original VC-MRI method, estimation using a ROI around the tumor of a sagittal 2D cine image resulted in the most accurate VC-MRI estimation compared to matching to the entire cine image, or global matching (13). For this study, the following regions were used for matching in the MM-FD algorithm: (I) global MM only; (II) ROI MM only; (III) global MM with global FD; (IV) global MM with ROI FD; (V) ROI MM with global FD; (VI) ROI MM with ROI FD. Global refers to matching to the entire cine image and ROI refers to only matching to an ROI around the tumor in the optimization. MM only means only optimizing with the MM method described in section “MM”. and FD refers to using the FD optimization described in section “FD”.
Effect of slice orientation, slice number and slice location
To evaluate the effect of slice orientation on VC-MRI estimation accuracy, sagittal, coronal and axial slices were extracted. The following orientations were investigated: (I) multiple sagittal slices; (II) multiple axial slices; (III) multiple coronal slices; and (IV) sagittal, axial and coronal orthogonal slices.
To evaluate the effect of slice number, the following various slice numbers were investigated: (I) 30 sagittal slices; (II) 15 sagittal slices; (III) 10 sagittal slices; (IV) 20 axial slices; (V) 10 axial slices; (VI) 30 coronal slices; (VII) 15 coronal slices; (VIII) 10 coronal slices; (IX) 30 orthogonal slices: 10 axial, 10 sagittal, 10 coronal; (X) 15 orthogonal slices: 5 axial, 5 sagittal, 5 coronal. The difference in number of sagittal and coronal slices compared with axial slices is due to the fact that the SI direction of the images had a courser resolution. Figure 2A shows the distributions of 30, 15 and 10 uniformly distributed sagittal slices for visual comparison.
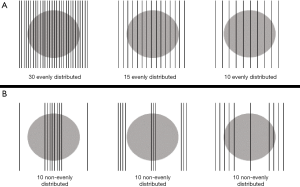
Different slice locations were extracted to evaluate the effect of slice location on VC-MRI estimation accuracy. Slices were uniformly taken throughout all locations of the tumor in the MRIprior volume, with slices extracted out to 15, 15 and 13 mm in the SI, AP and lateral directions surrounding the tumor. To evaluate the effect of slice location on the VC-MRI estimation accuracy, ten sagittal slices were extracted in the following locations: (I) slices distributed non-uniformly with a much higher density taken in the center of the tumor and only two slices extracted from the periphery; (II) high density of slices extracted in periphery and high density of slices extracted in center; and (III) higher density of slices extracted through periphery of tumor with one slice extracted from center. Figure 2B shows the slice distribution for the three slice locations described.
Patient study
The k-t SLR method was evaluated using four liver patients’ data, and accelerated VC-MRI was estimated using single-slice undersampled cine image and MM only due to unavailability of the multi-slice cine data. Data from four liver patients were acquired under IRB protocol. Details regarding the acquisition and image parameters for the patient study can be found in previous publications (5,13,14,19). To summarize, a fast steady state acquisition imaging technique (FIESTA) was used to acquire 2D axial and sagittal images continuously and then retrospectively sorted based on respiratory phases to generate 4D MRI. The 4D MRI reconstruction was done using either axial body area or sagittal body area as a respiratory surrogate (19,20). 2D axial, sagittal and coronal cines were acquired for 30 seconds with a temporal resolution of ~3 frames/s. The image acquisition parameters were repetition time (TR)/echo time (TE): 3.005 ms/1.128 ms; field of view (FOV): (300–480) × (360–480) mm; flip angle: 50 degrees; slice thickness: 5 mm, bandwidth: 976.562 Hz per pixel. The images were interpolated to 256×256 before further analysis (19). Direct Fourier Transformation was done on the axial, sagittal and coronal cine images and k-space data were undersampled and reconstructed based on k-t SLR described in section “FD”. Ten percent of fully sampled k-space data were acquired on a Cartesian coordinate system. Of the 10% of the undersampled data, 10% of that were acquired uniformly in the center k-space. The rest of k-space was randomly sampled. Each of the cine time-step slices had different random phase-encoded lines sampled. The time-steps, or the number of points in the temporal domain, for the four patients were 180, 90, 120, and 180, respectively.
Evaluation methods
For both the XCAT study and the patient study, the undersampled k-space data were reconstructed using the k-t SLR reconstruction method and an iterative MR reconstruction algorithm with total generalized variation (TGV) regularization (21) for comparison. Images were compared with the fully-sampled cine images.
For the XCAT study, the estimation accuracy of the VC-MRI technique was evaluated at the end of inspiration (EOI) phase since it had the largest deformation from MRIprior. The estimated and ground-truth tumor volumes were compared using volume percent difference (VPD) as defined in Equation [9], center of mass shift (COMS), as defined in Equation [10] and volume dice coefficient (VDC), as defined in Equation [11].
|
| [9] |
Where V is the tumor volume contoured in the estimated image and V0 is that contoured in the ground-truth image. The tumor volumes were contoured first based on image thresholding around a volume of interest around the tumor region, followed by manual tweaking slice by slice.
|
| [10] |
Δx, Δy, and Δz are center of mass distances from V to V0.
|
| [11] |
|V| and |V0|are the numbers of elements in the estimated volume and ground-truth volume, respectively.
For the patient studies, a previously developed ROI feature-based motion tracking method (5) was used to calculate and compare the tumor tracking based on VC-MRI and the 2D cine images acquired along different directions. Details regarding how the tracking errors were calculated can be found in previous publications (14).
Results
XCAT study
Undersampled cine MRI using k-t SLR reconstruction
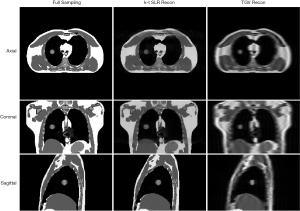
Figure 3 shows axial, coronal and sagittal cine images at a sample time step using fully sampled k-space data, undersampled k-space with the k-t SLR reconstruction method and undersampled k-space using the TGV reconstruction method used in previous work for the XCAT study. Both the k-t SLR and TGV reconstruction images were reconstructed using 10% of total k-space sampled. Table 2 shows results of VPD, VDC and COMS for VC-MRI estimation accuracy when the multi-slice on-board 2D sagittal cines were reconstructed based on TGV reconstruction and k-t SLR reconstruction. VC-MRI estimation was done using 30 sagittal cine images and both MM and FD.

Full table
ROI selection
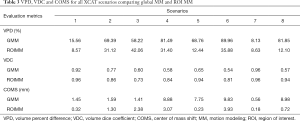
Table 3 shows VPD, VDC and COMS for all XCAT scenarios comparing global MM with ROI MM.
Full table
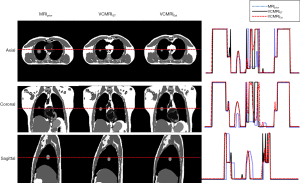
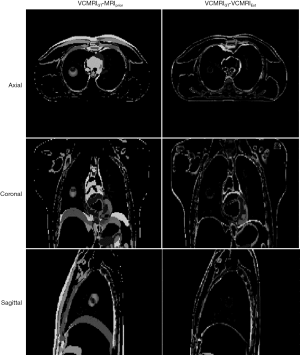
Table 4 shows VPD, VDC and COMS for all XCAT scenarios comparing global FD with ROI FD. For both global MM and ROI MM, global FD and ROI FD was done to test the effect of ROI selection on the FD optimization. Table 5 shows the VPD, VDC and COMS for all XCAT scenarios comparing ROIMM and ROIMMROIFD to emphasize the improvements that adding FD has on the VC-MRI accuracy. Figure 4 shows MRIprior, ground truth VC-MRI (VCMRIGT) and estimated VC-MRI (VCMRIEst) using ROIMMROIFD estimation, along with the corresponding profile curves for XCAT scenario 2. Figure 5 shows the corresponding subtraction images for Figure 4.

Full table
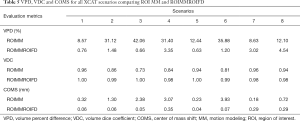
Full table
Effect of acquisition orientation
Table 6 shows VPD, VDC and COMS for all XCAT scenarios comparing different orientations and slice numbers. Sagittal, axial and coronal cine images were used to evaluate the effect of acquisition orientation. Orthogonal cine images were also used, which consisted of equal numbers of sagittal, axial and coronal cine images. For sagittal and coronal cine images, 30, 15 and 10 slices were used. For axial images, 20 and 10 slices were used. This was due to the fact that the resolution in the out-of-plane direction was coarser than the resolution in the in-plane direction. For the orthogonal orientation, 30 and 15 total slices were investigated. For the 30 orthogonal slices, 10 sagittal, 10 coronal and 10 axial images were used. For the 15 total slices, 5 sagittal, 5 coronal and 5 axial images were used.
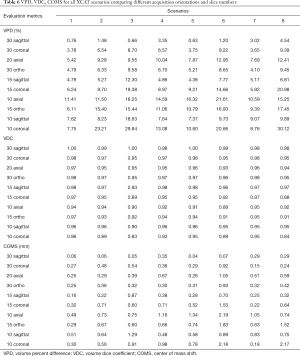
Full table
Effect of slice location
Table 7 shows VPD, VDC and COMS for all XCAT scenarios comparing different slice locations. For each of the estimation results, ten sagittal cine images were used. “Uniform” refers to evenly distributed slices. “Non-uniform1” refers to slices distributed non-uniformly with a much higher density taken in the center of the tumor and only two slices extracted from the periphery (bottom left image in Figure 2B). “Non-uniform2” refers to high density of slices extracted in periphery and high density of slices extracted in center (bottom middle image in Figure 2B), and “Non-uniform3” refers to higher density of slices extracted through periphery of tumor with one slice extracted from center (bottom right image in Figure 2B).
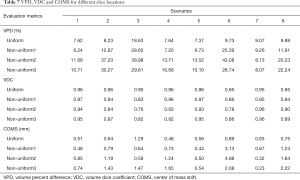
Full table
Patient study
Undersampled cine MRI using k-t SLR reconstruction
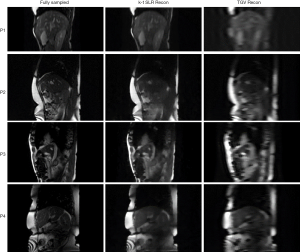
Figure 6 shows sample time-step images for sagittal slices for all four liver patients using full sampled k-space, undersampled k-space with the k-t SLR reconstruction method and undersampled k-space using the TGV reconstruction method used in previous work. Both the k-t SLR and TGV reconstruction images were reconstructed using 10% of total k-space sampled.
VC-MRI estimation
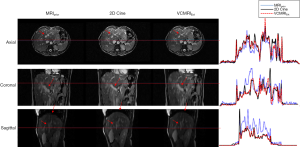
Figure 7 shows prior MRI image at the EOI phase, 2D cine at an EOEphase, estimated VC-MRI at an EOE phase and their normalized profile comparisons for patient 1. Figure 8 shows subtraction images between the estimated VC-MRI and the 2D cine for patient 1. Figure 9 shows the tumor tracking based on the fully sampled 2D cine images at different views, the estimated VC-MRI based on the fully sampled 2D cine images and the estimated VC-MRI based on the undersampled 2D cine images for average cycles in the lateral, SI and AP directions (13,14). The accelerated VC-MRI and non-accelerated VC-MRI were estimated based on sagittal cine images. The tracking along the SI and lateral directions was based using coronal orientation, and the tracking along the AP direction was based on sagittal orientation. Table 8 shows the mean tumor tracking errors and the Pearson correlation coefficients of the tumor tracking accuracy based on VC-MRI using fully sampled 2D sagittal cine images and accelerated VC-MRI using undersampled 2D sagittal cine images reconstructed using the k-t SLR method for each patient. All Pearson correlation coefficients were greater than 0.90.
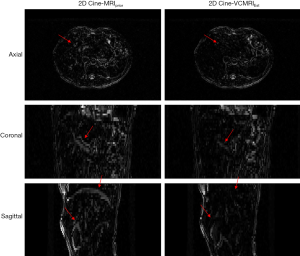

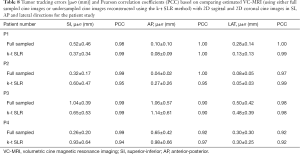
Full table
Discussion
The VC-MRI generation method using multiple undersampled 2D cine images, MM and FD can substantially improve the VC-MRI accuracy from the previous methods published in previous publications (13,14). This new method introduces FD models to correct for any errors in the MM, and it acquires multiple undersampled 2D cine images to provide adequate information for the FD estimation while maintaining the temporal resolution of the VC-MRI. Potentially, the accuracy of the FD model can be affected by the contrast of the image. Its speed is also slower than the MM method due to its large number of variables to be solved. The innovate k-t SLR reconstruction algorithm used to reconstruct the undersampled 2D cine k-space data used the spatio-temporal information of the data to reconstruct high quality cine images, while only acquiring 10% of total k-space. Using only 10% of total k-space was chosen based on previous work (6,14). In the MM optimization, only three modes from the PCA were used based on previous work that found that the first three principal motion modes are the most important and capture the majority of the deformations and using more modes does not result in better accuracy (15). The first three motion modes were also used in our previous work (13,14), which demonstrated their adequacy for VC-MRI estimation.
Results from the XCAT study showed using the k-t SLR reconstruction method compared to the TGV reconstruction method improved the VC-MRI accuracy by 67.20%, 2.34% and 59.79% for VPD, VDC and COMS, respectively, on average of all eight XCAT scenarios when using 30 sagittal cine images, based on Table 2. Results from Table 5 show the vast improvement adding FD has on the VC-MRI estimation for scenarios where MM only doesn’t result in accurate estimation, such as XCAT scenarios 2, 3, 4 and 6, where there is tumor size change or tumor positional changes from simulation to treatment. Results also showed that acquiring multiple sagittal cine images provided better VC-MRI estimation than acquiring multiple axial, coronal or orthogonal cine images. The more sagittal slices, the higher the VC-MRI accuracy. However, using ten sagittal slices provided adequate VC-MRI accuracy across all eight XCAT scenarios. Using ten cine slices, undersampled with each slice acquiring 10% of total k-space data, results in a maintained temporal resolution of VC-MRI when compared to using a single fully-sampled cine image. Based on results shown in Table 7, acquiring the multiple slices uniformly across the tumor region resulted in better accuracy than acquiring the slices non-uniformly distributed throughout the tumor region. It is important to note, however, that the non-uniform sampling strategies had large variations in VPD and COMS, showing that their performance is dependent on the on-board situation. In contrast, uniform sampling had more much robust accuracy across all scenarios. As the XCAT image voxel size is 1.875×1.875×3 mm3, a VPD ≤20% and COMS ≤2 mm were considered clinically acceptable tolerances (14). The uniform sampling strategy achieved accuracy within these tolerances for all XCAT scenarios, demonstrating its robustness for clinical applications. The reason for the large variation among VPD and COMS is that the among of anatomical information captured in non-uniform sampling is highly dependent on the tumor shape and location. If the tumor moves into the sparsely sampled region in certain scenarios, little information is captured for VC-MRI estimation, leading to large errors in VPD and COMS. In comparison, the uniform sampling ensures a consistent sampling density across the whole region regardless of the tumor location to ensure enough information is captured for VC-MRI estimation.
The method was evaluated using XCAT simulation to test the accuracy of using multiple 2D cine images and FD optimization. The XCAT study provides unique opportunities to evaluate the performance under different scenarios and provides a ground-truth image for quantitative evaluation. On-board scenarios were simulated to represent various respiratory and anatomical changes from simulation to treatment, such as tumor size change, breathing amplitude change and tumor positional change. There are other realistic situations that may clinically occur from simulation to treatment, such as tumor deformation, which is not feasible to implement with the XCAT simulation. The eight on-board scenarios that were used in this study are just a subset of possible common clinical occurrences. Four liver patients’ data were using to test the accuracy of the VC-MRI estimation when using a single-slice undersampled 2D cine MRI using the k-t SLR reconstruction method and MM only. The patient study provides a further evaluation of the estimated VC-MRI using real liver patient images with real respiratory motions. It is important to note the challenges with the patient study. First of all, only single-slice 2D cine MRI were acquired in the axial, sagittal and coronal planes, separately for all four liver patients. Therefore, it is currently impractical to test the VC-MRI method using multiple 2D cine images with FD. Also, it is challenging to establish a ground-truth VC-MRI for the patient studies, since currently there is no technique that is capable of acquiring real-time VC-MRI. Future studies should be implemented to acquire multiple 2D cine images using only 10% of k-space data for real liver patients, so that we can fully evaluate the VC-MRI estimation method using both MM and FD presented in this study. A prospective study will be conducted in the future once a new clinical protocol has been approved and enough patient data have been accrued. Also, this study showed that using an ROI in the estimation provided better VC-MRI accuracy than using the entire global image. This was tested on XCAT data, and future studies should be done to fully evaluate the effect ROI selection has on VC-MRI estimation using both XCAT and patient studies. In real patient studies, an ROI can be chosen based on using the planning PTV from the prior 4D image and expanding that by a given margin in every direction, to account for motion and set-up errors that may occur from simulation to treatment. Lastly, it is important to note that the XCAT evaluations were done on a lung phantom and the real patient evaluations were done on a liver patient. The different image qualities in lung and liver can have different impact on the accuracy of the VC-MRI. Future patient studies are needed to evaluate the accuracy the new VC-MRI technique in the lung.
The method proposed uses a FD optimization to fine-tune the DFM based on energy minimization and a data fidelity constraint. There are other techniques to estimation deformation, such as using artificial neural networks (22-25) or biomechanical models (26-28). Future work may be done in using other deformation optimization methods.
Additionally, this study used a novel k-t SLR method to reconstruct highly undersampled k-space data. There are other reconstruction methods that can be utilized in future studies to evaluate the effect the reconstruction has on the VC-MRI estimation accuracy (29-31). Another option to explore in the future would be to utilize ultrasound during radiotherapy to aid in the on-board information acquired. Giger et al. proposed an ultrasound-driven 4D MRI method for respiratory motion imaging, which could potentially be used in future studies to improve VC-MRI estimation (32).
In general, this new method further improves the accuracy of VC-MRI for different patient scenarios, making it a robust real-time volumetric MRI technique. These improvements of delivery accuracy can potentially improve the treatment outcome and pave the road to further margin reduction and dose escalation.
Conclusions
Studies showed that it is feasible to improve the VC-MRI accuracy while maintaining high temporal resolution using FD and multi-slice undersampled 2D cine images for real-time 3D target verification in radiation therapy.
Acknowledgments
Funding: The authors would like to acknowledge NIH grants R01CA184173 and R01EB028324.
Footnote
Conflicts of Interest: The authors have no conflicts of interest to declare.
Ethical Statement: This study was approved by the Institutional Review Board (No. Pro00032595).
References
- Keall PJ, Mageras GS, Balter JM, Emery RS, Forster KM, Jiang SB, Kapatoes JM, Low DA, Murphy MJ, Murray BR, Ramsey CR, Van Herk MB, Vedam SS, Wong JW, Yorke E. The management of respiratory motion in radiation oncology report of AAPM Task Group 76. Med Phys 2006;33:3874-900. [Crossref] [PubMed]
- Cervino LI, Chao AK, Sandhu A, Jiang SB. The diaphragm as an anatomic surrogate for lung tumor motion. Phys Med Biol 2009;54:3529-41. [Crossref] [PubMed]
- Zelefsky MJ, Kollmeier M, Cox B, Fidaleo A, Sperling D, Pei X, Carver B, Coleman J, Lovelock M, Hunt M. Improved clinical outcomes with high-dose image guided radiotherapy compared with non-IGRT for the treatment of clinically localized prostate cancer. Int J Radiat Oncol Biol Phys 2012;84:125-9. [Crossref] [PubMed]
- Soike M, Kilburn JM, Lucas JT, Ayala-Peacock D, Blackstock AW, Kearns WT, Hinson WH, Miller AT, Petty WJ, Urbanic JJ. Image Guided Radiation Therapy Results in Improved Local Control in Lung Cancer Patients Treated With Fractionated Radiation Therapy for Stage IIB-IIIB Disease. Int J Radiat Oncol Biol Phys 2013;87:S547-8. [Crossref]
- Cai J, Chang Z, Wang Z, Paul Segars W, Yin FF. Four-dimensional magnetic resonance imaging (4D-MRI) using image-based respiratory surrogate: a feasibility study. Med Phys 2011;38:6384-94. [Crossref] [PubMed]
- Sarma M, Hu P, Rapacchi S, Ennis D, Thomas A, Lee P, Kupelian P, Sheng K. Accelerating dynamic magnetic resonance imaging (MRI) for lung tumor tracking based on low-rank decomposition in the spatial-temporal domain: a feasibility study based on simulation and preliminary prospective undersampled MRI. Int J Radiat Oncol Biol Phys 2014;88:723-31. [Crossref] [PubMed]
- Dinkel J, Hintze C, Tetzlaff R, Huber PE, Herfarth K, Debus J, Kauczor HU, Thieke C. 4D-MRI analysis of lung tumor motion in patients with hemidiaphragmatic paralysis. Radiother Oncol 2009;91:449-54. [Crossref] [PubMed]
- von Siebenthal M, Szekely G, Gamper U, Boesiger P, Lomax A, Cattin P. 4D MR imaging of respiratory organ motion and its variability. Phys Med Biol 2007;52:1547-64. [Crossref] [PubMed]
- Remmert G, Biederer J, Lohberger F, Fabel M, Hartmann GH. Four-dimensional magnetic resonance imaging for the determination of tumour movement and its evaluation using a dynamic porcine lung phantom. Phys Med Biol 2007;52:N401-15.
- Cervino LI, Du J, Jiang SB. MRI-guided tumor tracking in lung cancer radiotherapy. Phys Med Biol 2011;56:3773-85. [Crossref] [PubMed]
- Mickevicius NJ, Paulson ES. Simultaneous orthogonal plane imaging. Magn Reson Med 2017;78:1700-10. [Crossref] [PubMed]
- Breuer FA, Blaimer M, Heidemann RM, Mueller MF, Griswold MA, Jakob PM. Controlled aliasing in parallel imaging results in higher acceleration (CAIPIRINHA) for multi-slice imaging. Magn Reson Med 2005;53:684-91. [Crossref] [PubMed]
- Harris W, Ren L, Cai J, Zhang Y, Chang Z, Yin FF. A Technique for Generating Volumetric Cine-Magnetic Resonance Imaging. Int J Radiat Oncol Biol Phys 2016;95:844-53. [Crossref] [PubMed]
- Harris W, Yin FF, Wang C, Zhang Y, Cai J, Ren L. Accelerating volumetric cine MRI (VC-MRI) using undersampling for real-time 3D target localization/tracking in radiation therapy: a feasibility study. Phys Med Biol 2017;63:01NT01. [Crossref] [PubMed]
- Zhang Y, Yin FF, Segars WP, Ren L. A technique for estimating 4D-CBCT using prior knowledge and limited-angle projections. Med Phys 2013;40:121701. [Crossref] [PubMed]
- Lu W, Chen ML, Olivera GH, Ruchala KJ, Mackie TR. Fast free-form deformable registration via calculus of variations. Phys Med Biol 2004;49:3067-87. [Crossref] [PubMed]
- Lingala SG, Hu Y, DiBella E, Jacob M. Accelerated dynamic MRI exploiting sparsity and low-rank structure: k-t SLR. IEEE Trans Med Imaging 2011;30:1042-54. [Crossref] [PubMed]
- Segars WP, Mahesh M, Beck TJ, Frey EC, Tsui BM. Realistic CT simulation using the 4D XCAT phantom. Med Phys 2008;35:3800-8. [Crossref] [PubMed]
- Yang J, Cai J, Wang H, Chang Z, Czito BG, Bashir MR, Yin FF. Four-dimensional magnetic resonance imaging using axial body area as respiratory surrogate: initial patient results. Int J Radiat Oncol Biol Phys 2014;88:907-12. [Crossref] [PubMed]
- Liu Y, Yin FF, Chang Z, Czito BG, Palta M, Bashir MR, Qin Y, Cai J. Investigation of sagittal image acquisition for 4D-MRI with body area as respiratory surrogate. Med Phys 2014;41:101902. [Crossref] [PubMed]
- Wang C, Yin FF, Kirkpatrick JP, Chang Z. Accelerated Brain DCE-MRI Using Iterative Reconstruction With Total Generalized Variation Penalty for Quantitative Pharmacokinetic Analysis: A Feasibility Study. Technol Cancer Res Treat 2017;16:446-60. [Crossref] [PubMed]
- de Vos BD, Berendsen FF, Viergever MA, Staring M, Išgum I. End-to-End Unsupervised Deformable Image Registration with a Convolutional Neural Network. arXiv:1704.06065v1 [cs.CV], 2017. doi: 10.1007/978-3-319-67558-9_24. [Crossref]
- Cao X, Yang J, Zhang J, Nie D, Kim MJ, Wang Q, Shen D. Deformable Image Registration based on Similarity-Steered CNN Regression. Med Image Comput Comput Assist Interv 2017;10433:300-8. [PubMed]
- Hu Y, Modat M, Gibson E, Ghavami N, Bonmati E, Moore CM, Emberton M, Noble JA, Barratt DC, Vercauteren T. Label-driven weakly-supervised learning for multimodal deformarle image registration. 2018 IEEE 15th International Symposium on Biomedical Imaging (ISBI 2018), 2017:1070-4.
- Pham J, Harris W, Sun W, Yang Z, Yin FF, Ren L. Predicting real-time 3D deformation field maps (DFM) based on volumetric cine MRI (VC-MRI) and artificial neural networks for on-board 4D target tracking: a feasibility study. Phys Med Biol 2019;64:165016. [Crossref] [PubMed]
- Zhang Y, Folkert MR, Huang X, Ren L, Meyer J, Tehrani JN, Reynolds R, Wang J. Enhancing liver tumor localization accuracy by prior-knowledge-guided motion modeling and a biomechanical model. Quant Imaging Med Surg 2019;9:1337-49. [Crossref] [PubMed]
- Velec M, Moseley JL, Svensson S, Hardemark B, Jaffray DA, Brock KK. Validation of biomechanical deformable image registration in the abdomen, thorax, and pelvis in a commercial radiotherapy treatment planning system. Med Phys 2017;44:3407-17. [Crossref] [PubMed]
- Al-Mayah A, Moseley J, Velec M, Brock K. Toward efficient biomechanical-based deformable image registration of lungs for image-guided radiotherapy. Phys Med Biol 2011;56:4701-13. [Crossref] [PubMed]
- Velikina JV, Samsonov AA. Reconstruction of dynamic image series from undersampled MRI data using data-driven model consistency condition (MOCCO). Magn Reson Med 2015;74:1279-90. [Crossref] [PubMed]
- Lingala SG, Jacob M. Blind compressive sensing dynamic MRI. IEEE Trans Med Imaging 2013;32:1132-45. [Crossref] [PubMed]
- Otazo R, Candes E, Sodickson DK. Low-rank plus sparse matrix decomposition for accelerated dynamic MRI with separation of background and dynamic components. Magn Reson Med 2015;73:1125-36. [Crossref] [PubMed]
- Giger A, Stadelmann M, Preiswerk F, Jud C, De Luca V, Celicanin Z, Bieri O, Salomir R, Cattin PC. Ultrasound-driven 4D MRI. Phys Med Biol 2018;63:145015. [Crossref] [PubMed]


