Kinetic modeling and analysis of dynamic bioluminescence imaging of substrates administered by intraperitoneal injection
Introduction
Bioluminescence imaging (BLI) has been found to have wide applications in life sciences and medical research due to its ease of use and high sensitivity (1-5). D-luciferin has often been used as a fluorescein substrate for BLI in vivo, with administration being carried out by intraperitoneal (IP) injection, intravenous (IV) injection, or subcutaneous (SC) injection (6,7). Amongst these methods, IP injection has seen expansive application because of its simple operational characteristics (8), with dynamic imaging studies having large advantages for diagnosis over traditional static imaging studies (9-11). With static BLI imaging, the relationship between tumor cell number and BLI signal intensity for the subcutaneously implanted tumor model has been validated (12,13), and the results show that they are positively correlated. Based on dynamic imaging, kinetic analysis models offer more quantitative information on the probe environment in vivo, including data on peak metabolic rates, clearance rates, and distribution volume, thus enabling the more comprehensive characterization of physiological and pathological features in the region of interest (ROI) (9,14-17). Therefore, it is necessary to conduct quantitative research into the use of dynamic BLI techniques for the real-time detection of tumor microenvironments and the evaluation of anti-cancer therapies.
Inoue et al. investigated the effect of the 3 injection routes on the results of in vivo BLI studies (6) while Keyaerts et al. compared the reproducibility of photon emissions from D-luciferin administered by IV versus IP injection routes (8). Inoue et al. carried out sequential imaging studies after D-luciferin injection, thus demonstrating the feasibility of using in vivo BLI to carry out longitudinal tumor growth assessment (18). These studies provide proof of the principle that dynamic BLI combined with kinetic models could be used for the quantitative evaluation of tumor growth. Sim et al. subsequently presented a quantitative analysis of tumor growth based on IP injection of D-luciferin (19) using kinetic parameters obtained from a two-compartment pharmacokinetic (PK) model to accurately describe and replicate the biodistribution of luciferin and growth kinetics of tumors. This method solves all the rate constants in the kinetic model. The fully sampled arterial plasma concentration is needed for the rate constants estimation (20), often suggesting a potentially elevated level of complexity and processing power for data analysis and parameter estimation. Researchers are often only concerned with parameters associated with the state of the tumor; therefore, we proposed that this model could potentially be simplified to reduce the level of computational complexity required.
This study employed a three-compartment PK model and standard Michaelis-Menten (M-M) kinetics to analyze BLI data generated from the metabolism of IP administered substrates by tumors in vivo. Instead of solving all the rate constants directly, we deduced the 4 differential equations describing the PK process into an exponential form and solved the macroparameters in it. The validity of this PK model was evaluated via an analysis of the dynamic BLI data generated in this paper and with the data from previously published longitudinal dynamic BLI studies.
Methods
Experimental details
Athymic nude male BALB/c mice (4–6 weeks, 18–22 g) were obtained from the Laboratory Animal Center, Fourth Military Medical University (FMMU), with the care and treatment of these animals performed in accordance with FMMU animal protocols. Tumors were introduced by injection of MKN28M-luc gastric cancer cells (~1×107 cells/mouse) via the caudal IV system and allowed to grow for around 4 weeks before dynamic imaging studies were carried out (21,22). The animals were imaged every 2 min for 60 min (23) with an IVIS Kinetic imaging system after IP injection of D-luciferin at a dose of 150 mg/kg. For each image frame, the camera exposure time was set to be 30 s. Consequently, 30 image frames were obtained after 1 h of observation.
Kinetic model
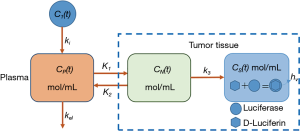
During typucal in vivo BLI, D-luciferin is injected into animals expressing firefly luciferase and is oxidized by luciferase, resulting in light emission. After IP injection, D-luciferin is absorbed through the peritoneum and reaches luciferase-expressing tumor tissues via the bloodstream (6). In this study, the concentration of D-luciferin in the tumor region was maintained in a stable range, thus enabling its metabolism to be modeled using standard M-M kinetics. A three-compartment PK model was used to structure the metabolic process (Figure 1) based on consideration of the following: (I) non-metabolized D-luciferin in the blood plasma which captures the nature of IP delivery through a first-order rate constant describing transit into the blood plasma (CP) from the peritoneum (CI), (II) non-metabolized D-luciferin in the tumor region (CN), and (III) metabolized D-luciferin in the tumor region (CS). ki is a measure of the extravasation rate of D-luciferin into the blood stream from the peritoneum, K1 reflects the extravasation rate of D-luciferin into the tumor region, k2 reflects the passage of D-luciferin back into the blood stream, and kel reflects the rate of D-Luciferin elimination in the plasma via other pathways like kidney filtration. k3 represents the decomposition rate of D-luciferin, which was considered to be equal to Vmax/Km, in accordance with the simplified M-M kinetics employed (24). Vmax is the maximum rate of D-luciferin to be oxidized by luciferase, and Km is known as the Michaelis constant. In addition, the tumor tissue, which is defined as a “bound” compartment by Sim et al., is divided into 2 compartments. One is the specific compartment composed of tumor cells expressing luciferase, and the D-luciferin is oxidized in this compartment; the other is the non-specific compartment composed of the intracellular tissues where no luciferase is present.
The equations used in Figure 1 are as follows:
|
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
According to the metabolic equations used for D-luciferin described in Sim et al. (19), the time-activity curves (TAC) of the BLI signals collected by the imaging instrument [set to L(t)] were proportional to the amount of substrate present in a defined tumor area that is metabolized within a unit time. This ratio was set to be R, with L(t) being defined as being equal to R multiplied by the time integral of CS(t). This enabled their relationship to be expressed as the following:
|
| [5] |
As bolus injections were used, the initial conditions of the above equations {Eq. [1]–Eq. [5]} can be set to CI(0) = CI0 ≠0 and CP(0) = CN(0) = CS(0) =0. Through the Laplace transform, the differential equations represented by Eq. [1]–Eq. [5] can be expressed as follows:
|
| [6] |
|
| [7] |
|
| [8] |
where C1(S) Cp(S) CN(S), and CS(S) are the Laplace transforms of C1(t), Cp(t), CN(t), and CS(S) respectively.
From Eq. [6] to Eq. [8], the CS(S) can be represented as follows:
|
| [9] |
With inverse Laplace transform and integration operation, we can get the time-domain expression as follows:
|
| [10] |
The factors A and α+β+ki are the parameters of interest, which correspond to the magnitude of the detected signal and the total sum of the kinetic rate constants (SKRC).
Image and data analysis
The proposed model was validated by both the dynamic BLI data of MKN28M-luc xenograft mice and the published longitudinal dynamic BLI data of B16F10-luc xenograft mice taken from the work of Sim et al. (19). For the MKN28M-luc xenograft mice data, the tumor area in the white light image was chosen to be the ROI. Identification of ROI and analysis of dynamic BLI data were conducted using Living Image 4.5 software (PerkinElmer, USA) and MATLAB 2015b (The MathWorks, USA), respectively. Mean values of the BLI signals (×105 photons/cm2/s) in each ROI were calculated to give the corresponding TAC, with data fitting carried out using the Curve Fitting Toolbox in MATLAB and R-square values to test for goodness of fit.
Statistical analysis
Results were expressed as mean values with standard deviations (means ± SD), with statistical significance evaluated using one-way analysis of variance (ANOVA) and least significant difference (LSD) tests. P values ≤0.05 were considered to correspond to statistically significant differences.
Results
Validation of the model
Figure 2A shows the representative dynamic BLI imaging results, which are all displayed using the same color scale. These results show that the intensity and range of the BLI signals gradually increased over time, reaching peak values around 15 min after imaging was commenced, before gradually decreasing in intensity. The corresponding raw TAC of the BLI signals is illustrated in Figure 2B, which shows a similar trend to the results in Figure 2A. The integrals of the TAC data of the BLI signals are displayed in Figure 2C, demonstrating that the PK model exhibited excellent data fitting properties (R-square =1).
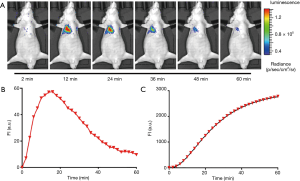
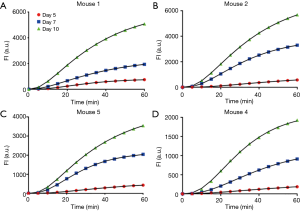
Figure 3 shows the integral TACs of the BLI signals and the results of their fitting using longitudinal dynamic BLI data from 4 mice that were published by Sim et al. The three-compartment PK model constructed in this study demonstrated an excellent fitting ability for all integral TACs of the BLI signals (all R-square >0.99). In addition, all integral TACs had a relatively shallow and prolonged upward trend, which indicates that the metabolism of D-luciferin was slow and stable. Differences in the integration value of TACs over successive days imply that this BLI technique can be used to measure changes in the uptake and metabolism of D-luciferin as the tumor grows.
Application of the fitting model to previously published data
The statistical results obtained for the 2 kinetic parameters are shown in Figure 4A,B, which show that both kinetic parameters increased as the tumor grew. Although the increase in the A value was most obvious, significant statistical differences occurred for all 3 groups (ANOVA, P<0.05). However, the SKRC value became smaller over time, and there was no significant statistical difference between the groups (LSD, all P>0.05). The relationship between the A value and tumor volume (TV) was analyzed statistically, which revealed that there was a good linear relationship on a logarithmic scale [lg(A) =0.06745 lg(TV)+0.8107], with the slope of the line being about 0.6745≈2/3. As the tumor is usually assumed to be spherical or elliptical (6,25), it may be induced that any increase in macroparameter A was linearly related to the tumor surface area (A ≈ TV2/3).

Discussion
The BLI of cellular systems gives better imaging results, because this technique affords shorter luminous half-life and higher image signal-to-noise ratio than can be achieved using conventional fluorescence studies (26). During BLI, a fluorescein substrate that decomposes over a short period can be used to monitor cellular processes, while causing less adverse effects on the normal biochemical processes of the organism (27). For continuous observation, the IP injection of a luminous substrate can be used to conduct longitudinal studies by dynamic optical imaging. At the same time, dynamic optical imaging combined with kinetics analysis can estimate various parameters associated with metabolic rate.
Therefore, a three-compartment PK model suitable for monitoring the IP injection of luminescent substrates was developed and validated using real experimental data and previously published longitudinal dynamic BLI data. These results indicate that the three-compartment PK model can provide excellent fitting for all integral TACs of the BLI signals (all R-square >0.99), enabling 2 kinetic parameters to be obtained that effectively reflect the growth rate of the tumor. Compared with traditional static BLI, the use of dynamic BLI combined with this kinetic model can supply useful PK information for investigating tumor growth.
The quantitative method proposed by Sim et al. can be used to accurately determine all kinetic parameters. However, the level of complexity that the data analysis procedures requires is significantly higher than our model. Our model is only concerned with determining the combination of some of the PK parameters (called a macroparameters) associated with the state of the tumor, which significantly reduces its computational complexity. The PK parameter solving process employed is simple, enabling the Optimization toolbox of MATLAB 2015b to be used for analysis. As can be seen from Figure 4, the A values produced using this analysis represent a meaningful PK parameter that accurately reflects the state of tumor growth state.
Consequently, the A value can be considered as an indicator of tumor surface area, enabling it to be used as a prognostic factor in primary and recurrent glioblastoma irradiated with Ir implantation (28). In addition, the value of CI (0) is related to the injection dose and is regarded as a constant. With fixed R and ki, the macro-parameter A reflects changes of K1. It should be noted that K1 is similar to kbt in Sim’s model, where kbt correlates to the measured tumor volume. One possible reason for this difference is that the third formula in their model does not reflect the rate of decomposition of the substrate (that is, the PK parameter k3 in our model).
The SKRC value may be used to find the tumor growth state; however, there was no significant statistical difference between the groups (LSD, all P>0.05) investigated. This may be because the SKRC value for this model contained too many parameters to reduce variance. The three-compartment PK model constructed in this study demonstrated excellent fitting for all the integral TACs of the BLI signals (all R2 >0.99) measured. These results suggest that this model can be used to more accurately estimate the metabolic trend of a substrate, which would be greatly beneficial for generating reference values when multiple substrate injections are needed.
To further confirm the estimated tumor growth by the proposed model, it is necessary to perform the histology or other imaging modalities. In our future in vivo longitudinal research, we will confirm the tumor growth rate by small animal magnetic resonance imaging (MRI) or positron emission tomography (PET). In dynamic BLI, the exposure time and the animal’s skin conditions play a key role in the absolute luminescence intensity. Nevertheless, according to our earlier work (16), the estimated parameters in the kinetic models exhibited no statistical difference as the exposure time varied in dynamic fluorescence imaging. As the exposure time was kept unchanged during our experiment, and the skin condition affected the absolute luminescence intensity, we did not incorporate them into the proposed kinetic model. However, a study that does consider these parameters for the model is warranted in future work.
Conclusions
In conclusion, a three-compartment model was developed to analyze the pharmacokinetics of substrates administered by IP injection in dynamic BLI. To simplify the parameter estimation, we deduced the differential equations describing the model into an exponential expression where macroparameters are used, and the macroparameters were estimated using the nonlinear fitting method. The validity of this three-compartment model was confirmed by the analysis of dynamic BLI data of MKN28M-luc xenograft mice and the previously published longitudinal dynamic BLI data. Results show that this model exhibits an excellent fit to the data obtained, with 2 kinetic macroparameters being obtained that effectively reflect the rate of tumor growth in vivo. The presented PK model may be an effective tool for dynamic BLI analysis and can be used to monitor the response of tumors to treatment.
Acknowledgments
Funding: This work was supported in part by the National Key R&D Program of China (No. 2018YFC0910602), the National Natural Science Foundation of China (No. 81571725, 81627807, 11727813, 81871397, and 91859109), the Fok Ying-Tong Education Foundation of China (No. 161104), the Program for the Young Top-notch Talent of Shaanxi Province, the Research Fund for Young Star of Science and Technology in Shaanxi Province (No. 2018KJXX-018), the Best Funded Projects for the Scientific and Technological Activities for Excellent Overseas Researchers in Shaanxi Province (No. 2017017), and the Fundamental Research Funds for Central Universities (No. JB171202, JB171206, and JB181203).
Footnote
Conflicts of Interest: The authors have no conflicts of interest to declare.
Ethical Statement: This study was approved by the Xi’an Jiaotong University Animal Care and Use Committee, China (No. XJTULAC2016-412).
References
- O'Farrell AC, Shnyder SD, Marston G, Coletta PL, Gill JH. Non-invasive molecular imaging for preclinical cancer therapeutic development. Br J Pharmacol 2013;169:719-35. [Crossref] [PubMed]
- Wurdinger T, Badr C, Pike L, de Kleine R, Weissleder R, Breakefield XO, Tannous BA. A secreted luciferase for ex-vivo monitoring of in vivo processes. Nat Methods 2008;5:171-3. [Crossref] [PubMed]
- O'Neill K, Lyons SK, Gallagher WM, Curran KM, Byrne AT. Bioluminescent imaging: a critical tool in pre-clinical oncology research. J Pathol 2010;220:317-27. [PubMed]
- Ignowski JM, Schaffer DV. Kinetic analysis and modeling of firefly luciferase as a quantitative reporter gene in live mammalian cells. Biotechnol Bioeng 2004;86:827-34. [Crossref] [PubMed]
- Miao Y, Chen Z, Li SC. Functional endoscopy techniques for tracking stem cell fate. Quant Imaging Med Surg 2019;9:510-20. [Crossref] [PubMed]
- Inoue Y, Kiryu S, Izawa K, Watanabe M, Tojo A, Ohtomo K. Comparison of subcutaneous and intraperitoneal injection of D-luciferin for in vivo bioluminescence imaging. Eur J Nucl Med Mol Imaging 2009;36:771-9. [Crossref] [PubMed]
- Dai Y, Wang G, Chen D, Yin J, Zhan Y, Nie Y, Wu K, Liang J, Chen X. Intravenous administration-oriented pharmacokinetic model for dynamic bioluminescence imaging. IEEE Trans Biomed Eng 2019;66:843-7. [Crossref] [PubMed]
- Keyaerts M, Verschueren J, Bos TJ, Tchouate-Gainkam LO, Peleman C, Breckpot K, Vanhove C, Caveliers V, Bossuyt A, Lahoutte T. Dynamic bioluminescence imaging for quantitative tumour burden assessment using IV or IP administration of D: -luciferin: effect on intensity, time kinetics and repeatability of photon emission. Eur J Nucl Med Mol Imaging 2008;35:999-1007. [Crossref] [PubMed]
- Zhu L, Guo N, Li Q, Ma Y, Jacboson O, Lee S, Choi HS, Mansfield JR, Niu G, Chen X. Dynamic PET and Optical Imaging and Compartment Modeling using a Dual-labeled Cyclic RGD Peptide Probe. Theranostics 2012;2:746-56. [Crossref] [PubMed]
- Tichauer KM, Wang Y, Pogue BW, Liu JT. Quantitative in vivo cell-surface receptor imaging in oncology: kinetic modeling & paired-agent principles from nuclear medicine and optical imaging. Phys Med Biol 2015;60:R239-69. [Crossref] [PubMed]
- Pogue BW, Samkoe KS, Hextrum S, O’Hara JA, Jermyn M, Srinivasan S, Hasan T. Imaging targeted-agent binding in vivo with two probes. J Biomed Opt 2010;15:030513. [Crossref] [PubMed]
- Sweeney TJ, Mailander V, Tucker AA, Olomu AB, Zhang W, Cao YA, Neigrin RS, Contag CH. Visualizing the kinetics of tumor-cell clearance in living animals. Proc Natl Acad Sci U S A 1999;96:12044-9. [Crossref] [PubMed]
- Genevois C, Loiseau H, Couillaud F. In Vivo Follow-up of Brain Tumor Growth via Bioluminescence Imaging and Fluorescence Tomography. Int J Mol Sci 2016;17:E1815. [Crossref] [PubMed]
- Dai Y, Chen X, Yin J, Kang X, Wang G, Zhang X, Nie Y, Wu K, Liang J. Investigation of injection dose and camera integration time on quantifying pharmacokinetics of a Cy5.5-GX1 probe with dynamic fluorescence imaging in vivo. J Biomed Opt 2016;21:86001. [Crossref] [PubMed]
- Davis SC, Samkoe KS, Tichauer KM, Sexton KJ, Gunn JR, Deharvengt SJ, Hasan T, Pogue BW. Dynamic dual-tracer MRI-guided fluorescence tomography to quantify receptor density in vivo. Proc Natl Acad Sci U S A 2013;110:9025. [Crossref] [PubMed]
- Dai Y, Yin J, Huang Y, Chen X, Wang G, Liu Y, Zhang X, Nie Y, Wu K, Liang J. In vivo quantifying molecular specificity of Cy5.5-labeled cyclic 9-mer peptide probe with dynamic fluorescence imaging. Biomed Opt Express 2016;7:1149-59. [Crossref] [PubMed]
- Dai Y, Chen X, Yin J, Wang G, Wang B, Zhan Y, Nie Y, Wu K, Liang J. Investigation of the influence of sampling schemes on quantitative dynamic fluorescence imaging. Biomed Opt Express 2018;9:1859. [Crossref] [PubMed]
- Inoue Y, Kiryu S, Watanabe M, Tojo A, Ohtomo K. Timing of imaging after D-luciferin injection affects the longitudinal assessment of tumor growth using in vivo bioluminescence imaging. Int J Biomed Imaging 2010;2010:471408.
- Sim H, Bibee K, Wickline S, Sept D. Pharmacokinetic modeling of tumor bioluminescence implicates efflux, and not influx, as the bigger hurdle in cancer drug therapy. Cancer Res 2011;71:686-92. [Crossref] [PubMed]
- Feng D, Ho D, Chen K, Wu LC, Wang JK, Liu RS, Yeh SH. An evaluaiton of the algorithms for determing local cerebral metabolic rates of glucose using positron emission tomography dynamic data. IEEE Trans Med Imaging 1995;14:697-710. [Crossref] [PubMed]
- Wang L, Wu Y, Lin L, Liu P, Huang H, Liao W, Zheng D, Zuo Q, Sun L, Huang N, Shi M, Liao Y, Liao W. Metastasis-associated in colon cancer-1 upregulation predicts a poor prognosis of gastric cancer, and promotes tumor cell proliferation and invasion. Int J Cancer 2013;133:1419-30. [Crossref] [PubMed]
- Chen D, Liu G, Xu N, You X, Zhou H, Zhao X, Liu Q. Knockdown of ARK5 Expression Suppresses Invasion and Metastasis of Gastric Cancer. Cell Physiol Biochem 2017;42:1025-36. [Crossref] [PubMed]
- Evans MS, Chaurette JP, Adams ST, Reddy GR, Paley MA, Aronin N, Prescher JA, Miller SC. A synthetic luciferin improves bioluminescence imaging in live mice. Nat Methods 2014;11:393-5. [Crossref] [PubMed]
- Gurfinkel M, Shi K, Wei W, Li C, Sevick-Muraca EM. Quantifying molecular specificity of αvβ3 integrin-targeted optical contrast agents with dynamic optical imaging. J Biomed Opt 2005;10:034019. [Crossref] [PubMed]
- Niu G, Zhu L, Ho DN, Zhang F, Gao H, Quan Q, Hida N, Ozawa T, Liu G, Chen X. Longitudinal Bioluminescence Imaging of the Dynamics of Doxorubicin Induced Apoptosis. Theranostics 2013;3:190-200. [Crossref] [PubMed]
- Welsh DK, Kay SA. Bioluminescence imaging in living organisms. Curr Opin Biotechnol 2005;16:73-8. [Crossref] [PubMed]
- de Rautlin de la Roy Y, Messedi N, Grollier G, Grignon B. Kinetics of bactericidal activity of antibiotics measured by luciferin-luciferase assay. J Biolumin Chemilumin 1991;6:193-201. [Crossref] [PubMed]
- Lebioda A. Tumour surface area as a prognostic factor in primary and recurrent glioblastoma irradiated with 192Ir implantation. Rep Pract Oncol Radiother 2008;13:15-22. [Crossref]