Improving multi-channel compressed sensing MRI with reweighted l1 minimization
Introduction
Imaging speed in magnetic resonance imaging (MRI) is an important issue, especially in clinical settings because shortening the scan time can reduce the cost and increase throughput and patient’s comfort. However, the data acquisition is practically limited by hardware capability and signal-to-noise ratio (SNR) factors. Compressed sensing (CS) is a method that allows a sparse signal to be reconstructed from a set of randomly under-sampled projection data (1,2). It has been demonstrated that CS is useful for speeding up MRI acquisition, where data is collected in the k-space, i.e., Fourier space (3).
Multi-channel imaging using array receiver system offers improved SNR (4,5) or accelerated speed with parallel imaging (PI). Therefore, integrating CS and PI are expected to further improve the MRI quality and/or speed (6-10). In doing so, CS and PI are coupled in a large linear system or decoupled in separated steps. In the latter case, CS algorithm is applied to each channel individually, then the final image can be reconstructed using the sensitivity encoding method (11) or a root-sum-of-squares method (12). In addition, the correlations of distributed compressed sensing has also been applied in the system to improve the image quality (13). In all the aforementioned methods, image reconstructions involves minimizing the l1 norm of a sparse image representation in certain domains, such as the wavelet domain or total variation (TV). Since l1 is an approximation of the sparsity measurements, i.e., l0 norm of the sparse domain, there have been efforts to further improve l1 minimization so that it will be closer to the l0 minimization solution.
In this paper, we develop a method that reconstructs MRI image from multi-channel data in the CS framework with a reweighted l1 minimization. The main feature of the new method is that it uses an iterative, reweighted l1 minimization method to perform the CS reconstruction of multi-channel MRI data. The method was compared with two existing multi-channel CS reconstruction methods using computer simulations and in vivo MRI data. The results show that the proposed method can provide an improved reconstruction quality at a slightly increased computation cost. This paper is developed based on preliminary work presented in a conference abstract (14).
Methods
The array MR receiver system consists of a set of receiver channels, which are individually connected to decoupled coil elements. With an array receiver system, a k-space data set yk, k = 1, 2,…, c, will be acquired from each channel. In applying CS reconstruction, each channel can be formulated as an underdetermined system, yk=Φxk, where Φ is an operator of randomly under-sampled Fourier Transform implemented by the phase-encoding and frequency-encoding gradients. The CS theory states that an image xk can be recovered from the incomplete k-space data yk if it is sufficiently sparse. However, even the image itself is not sparse, it can often be transformed to a sparser domain and there is high probability that the image can be recovered. A commonly used sparsifying transform is the gradient operators; i.e., the image reconstruction can be achieved by solving the following convex optimization problem,
[1] |
where , where (Dxk)i,j represents the forward difference between adjacent pixels defined as (xi+1,j–xi,j, xi,j+1–xi,j). Here, total variation (TV) is considered as the l1 norm of the magnitudes of the gradients. This formulation follows the method described in (12).
After all channels images are reconstructed. They are combined using a root-sum-of-squares method. The overall reconstruction procedure is shown in Figure 1. As shown, under-sampled k-space data is fed to the use of l1 minimization algorithm, whose outputs are recursively calculated as the weights of the next iteration and finally produce the final image.
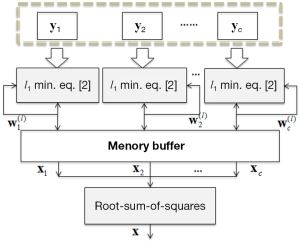
In this paper, we utilize the reweighted l1 minimization algorithm (15) to enhance the CS image reconstruction from multi-channel data. To solve the minimization problem in Eq. [1], it is rewritten as a second-order cone problem with weights:
where the weights are set to be inversely proportional to the signal magnitude. Based on the theory of reweighted l1 minimization, the larger entries of wk, i.e., where signal magnitude is close to zero, will discourage small entries of the reconstructed image xk. In the proposed method, small weights are calculated from the previous reconstructed images. As a result, the weights can be considered as iterative parameters in the convex relaxation to improve the image reconstruction.
Specifically, each image xk is reconstructed as follows.
(I) Set the iteration count, l=1 and the initial weight, for i=1,…,m and j=1,…,n. Note that
is the weight on pixel (i, j).
(II)Solve the weighted l1 minimization problem
[2] |
This was performed using a home-made Matlab program by modifying the l1-magic software package (16).
(III) Update the weights:
[3] |
The parameter ε is a small positive number to prevent zero-valued denominator. In this paper, it is set to 0.2 of the normalized received data.
(IV) If l<lmax, increase l and go to step 2.
Finally, all the reconstruction images are combined by the root-sum-of-squares of all channel images.
[4] |
To test the proposed method, both simulated and in vivo data were used. The k-space data of four channels were simulated using the ‘Shepp-Logan’ phantom with an image size of 128×128. The individual channel sensitivities are assumed to be shifted 2-dimension Gaussian functions. The individual channel data were under-sampled in the k-space with radial sampling pattern. The under-sampling factor was about 15%, which meant only 15% of the total data were used in reconstructions. Finally, an 8-channel in vivo brain MR data set was acquired and tested. The k-space data with an image size of 256×256 from each-channel were acquired in full field-of-view, i.e., without under-sampling. Then, the radial sampling was simulated by decimation with an under-sampling factor of 25%. Based on the same sampling factor, the reconstruction image using the proposed method was compared with two methods: (I) conventional TV minimization (l1 minimization with no reweighted iterations); and (II) a method combined in (9), which combine CS with SPACE-RIP (Sensitivity Profiles from an Array of Coils for Encoding and Reconstruction In Parallel).
The normalized means square error (NMSE) was used to evaluate the performance and defined as follows
[5] |
Note that is the referenced image, which is reconstructed from the fully sampled data in the k-th channel.
Results
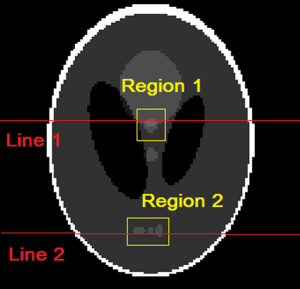
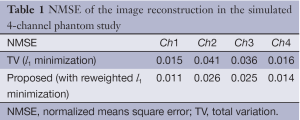
To show the quantitative improvement of the proposed approach the NMSE of the reconstructions by the conventional TV (l1 minimization) and the proposed method is shown in Table 1. It shows that the proposed method has a lower NMSE than the conventional l1 minimization algorithm since low NMSE represents less reconstruction error; the proposed method is superior in this study. Figures 2-5 show the images and reconstruction details in the simulated phantom study. Figure 2 indicates two regions and two lines on the original phantom study, which are used to compare the reconstructed details and resolutions. The comparisons of the reconstruction details are show in Figures 3 and 4. As the highlight region 1 and region 2 shown in Figure 3, the proposed method can recover more details of the edges pointed by the arrows. This is also illustrated in Figure 4, which displays the surface plots of the same corresponding zoom-in images shown in Figure 3. The three-dimension angle of view is also indicated along the arrows shown in Figure 3. Besides recovering sharper edges, it is observed that the proposed method can eliminate the staircase artifacts around smooth area noted by these arrows of Figure 4. In addition, the difference between the original image and the reconstructed image, i.e., reconstruction errors along line 1 and line 2, are shown in Figure 5. Again, it demonstrates the proposed method yields the reduced reconstruction error.
Full table

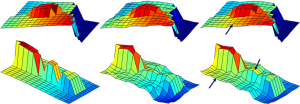
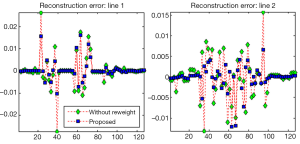
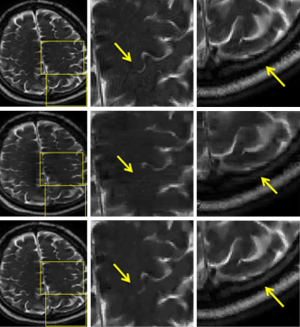
Figure 6 compares the image reconstructions in an 8-channel in vivo brain imaging experiment. Here, the left column represents the reconstructed images from the fully sampled data, the method in (9), where CS is integrated into a large linear system of multiple receiver coils, and the proposed method, respectively. The middle and right columns show the zoom-in views of the regions highlighted. To facilitate visualization, arrows are placed at the area where significant differences can be observed. As can be seen, higher fidelity in details and sharper features are obtained with the proposed method. Note that all images in the middle and bottom rows are reconstructed from 25% of the fully sampled data.
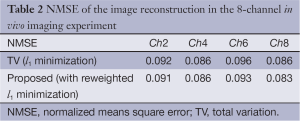
A comparison between the proposed method and the conventional TV minimization is shown in Table 2 (only even channels are shown). The performance in terms of NMSE is shown. One can see that the proposed method has smaller quantitative reconstruction error.
Full table
Discussion
A new improved reconstruction method for compressive sensing MRI with multi-channel phased array data was presented. In this method, the image is reconstructed using the reweighted l1 minimization algorithm in a channel-by-channel fashion. The simulated experimental results show that the new method can provide an improved image quality from the same data. On the other hand, the new algorithm requires more iterations than the conventional l1 minimization algorithm. This might pose a problem when immediate delivery of images is preferred. In such cases, using multi-core processors such as graphic processing unit (GPU) can be applied to parallelize the reconstruction and to shorten the reconstruction time. The proposed method can also be applied to the other CS methods where l1 minimization is used.
Acknowledgements
This work was supported in part by the NSF (National Science Foundation) under award number 0748180. Any opinions, findings and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect those of the NSF.
Disclosure: The authors declare no conflict of interest.
References
- Candès EJ, Romberg J, Tao T. Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information. IEEE Trans Inf Theory 2006;52:489-509.
- Donoho DL. Compressed sensing. IEEE Trans Inf Theory 2006;52:1289-306.
- Lustig M, Donoho D, Pauly JM. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magn Reson Med 2007;58:1182-95. [PubMed]
- Roemer PB, Edelstein WA, Hayes CE, et al. The NMR phased array. Magn Reson Med 1990;16:192-225. [PubMed]
- Wright SM, Wald LL. Theory and application of array coils in MR spectroscopy. NMR Biomed 1997;10:394-410. [PubMed]
- King K. Combining compressed sensing and parallel imaging. In Proceedings of the 16th Annual Meeting of ISMRM. Toronto, 2008:1488.
- Wu B, Millane R, Watts R, et al. Applying compressed sensing in parallel MRI. in Proceedings of the 16th Annual Meeting of ISMRM. Toronto, 2008:1480.
- Liu B, Sebert F, Zou Y, et al. SparseSENSE: randomly-sampled parallel imaging using compressed sensing. In Proceedings of the 16th Annual Meeting of ISMRM. Toronto, 2008:3154.
- Zhao C, Lang T, Ji J. Compressed sensing parallel imaging. In Proceedings of the 16th Annual Meeting of ISMRM. Toronto, 2008:1478.
- Marinelli L, Hardy C, Blezek D. MRI with accelerated multi-coil compressed sensing. In Proceedings of the 16th Annual Meeting of ISMRM. Toronto, 2008:1484.
- Liang D, Liu B, Wang J, et al. Accelerating SENSE using compressed sensing. Magn Reson Med 2009;62:1574-84. [PubMed]
- Chang CH, Ji J. Compressed sensing MRI with multichannel data using multicore processors. Magn Reson Med 2010;64:1135-9. [PubMed]
- Liang D, King K, Liu B, et al. Accelerating SENSE using distributed compressed sensing. In Proceedings of the 17th Annual Meeting of ISMRM. Honolulu, 2009:377.
- Chang CH, Ji J. Improved compressed sensing MRI with multi-channel data using reweighted minimization. In Proceedings of International Conference of the IEEE Engineering in Medicine and Biology Society. Argentina, 2010:875-8.
- Candès EJ, Wakin MB, Boyd SP. Enhancing sparsity by reweighted 1 minimization. J Fourier Anal Appl 2008;14:877-905.
- Candès EJ, Romberg J. Available online: http://users.ece.gatech.edu/~justin/l1magic/, accessed on March 3rd, 2014.