An unsupervised semi-automated pulmonary nodule segmentation method based on enhanced region growing

Introduction

According to reports from the World Health Organization (WHO) and major cancer research centers, lung cancer has the world’s highest cancer mortality rate (1). A status report produced by the International Agency for Research on Cancer states that lung cancer remains the leading cause of cancer incidence and mortality, with 2.1 million new lung cancer cases and 1.8 million deaths predicted worldwide in 2018, representing close to 1 in 5 (18.4%) cancer deaths (2). However, early detection with computed tomography (CT) has been shown to help reduce lung cancer-specific mortality (3). In medicine, a lung nodule is defined as a focal opacity whose largest diameter is between 3 mm and 3 cm in length (4). Nodules with diameters less than 3 mm are known as micronodules (5).

In general, the radiologist forms a diagnosis by reading the CT image in digital imaging and communications in medicine (DICOM) format (6). The radiologist quickly searches through all the images to determine the accuracy of suspected pulmonary nodules with obvious features and then combines those images of the previous and subsequent consecutive images to analyze the size, characteristic changes, and signs of the lung nodules in the corresponding images. This kind of reading process takes quite some time and puts intense pressure on radiologists, especially when they have been working all day and must repeatedly switch between various conditions. Hence, computer technology is required to quickly and accurately segment/mark lung nodule images to assist radiologists in diagnosing diseases (7-9). This supplementary approach has been used for applications such as lung parenchyma density analysis (10,11), airway analysis (12,13), and pulmonary nodule detection (14-16). The application of computer-aided detection in pulmonary nodules segmentation with CT images and nodule type and characteristics determination would be helpful for the early detection of lung cancer and tumor diagnosis.

A general process of automatic methods for pulmonary nodule segmentation usually includes image acquisition, preprocessing, pulmonary parenchyma segmentation, focal region extraction, optimization, and feature extraction (17,18).

Many researchers have studied image segmentation (19-22). Some approaches identify lesions based on preset shape-information of the target area and use machine learning-based algorithms to detect lesion features (23). However, many segmentation algorithms require image denoising, which would severely affect the processing speed as considerable manual input is required. Also, some automatic segmentation algorithms require manual operations in preprocessing, such as range determination and threshold testing (24-26). These result in extremely long segmentation time and reduce the accuracy of results. Therefore, these segmentation algorithms have extremely limited practical value. Other studies use images of a single lesion or CT-enhanced scan image for segmentation, and thus the results are not reproducible. Furthermore, those automatic segmentation algorithms also require a large amount of segmented lesion data for prior learning, which takes a lot of pre-work, and the quality of the data used for model training directly affects the quality of the model.

In this paper, a new semi-automated algorithm of lung nodule segmentation is introduced. It links the clinical manifestation of the lesion to image features via an image processing method. The results of ReGANS were compared with other computer-based segmentation techniques and manual segmentation performed by radiologists to validate the efficiency and accuracy, evaluated by probability rand index (PRI) (27), global consistency error (GCE) (28), and variation of Information (VoI) (28). Multiple types of nodules were also randomly selected for an experiment to prove its robustness.

Methods

The study design was approved by the Shanghai University of Medicine and the Health Sciences Ethics Review Board. The need for informed consent was waived.

Dataset

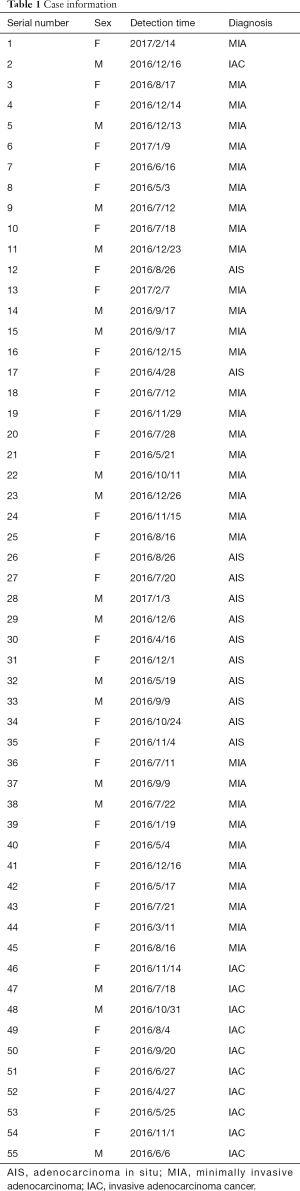
Two datasets were used in this study. The first one was generated at the Shanghai Public Clinical Health Center (SPCHC) and was collected between 2016 and 2017 (Table 1). An unenhanced chest CT exam was performed for the entire lung scan of each patient with a United-Imaging 760 CT device (42–126 mA 120 kV, slice thickness of 1 mm) and a Siemens Emotion 16 CT device (34–123 mA, 130 kV, 1 mm) with a 512×512 resolution. A total of 55 sets of image data were collected with 407 CT images. Among them, 25 groups (166 CT images) were used in the analysis of the speed and accuracy of the method, and the remaining 30 groups (241 CT images) were used in further method robustness verification experiments. Two radiologists performed the diagnosis of the pulmonary nodule.

Table 1 Case information
Full table

Another dataset was taken from the The Lung Image Database Consortium Image Collection public data set (LIDC-IDRI) (https://wiki.cancerimagingarchive.net/display/Public/LIDC-IDRI). A total of 30 sets of image data with 234 CT images were randomly selected.

The snake (29), special processing named selective binary Gaussian filtering regularized level set (SBGFRLS) (30), and level-set (31) methods were compared to the ReGANS. These methods were partially modified with reference to the experimental environment and data. As the number of iterations was increased further, the time taken by the algorithm increased substantially without a significant gain in optimization performance. The Snake and level-set used 250 iterations. For the SBGFRLS method, the image was first cut into a small square centered on and fully containing the lung nodule, which in turn increased the speed of the algorithm. The region-growing algorithm in the ReGANS method involved the evaluation of the 8 neighboring voxels surrounding an initial seed point. These surrounding voxels were evaluated according to their similarity to the seed voxel. They were accepted or rejected based on a combination of an artificially set change rate from the starting point, the voxel value change rate of the region, and the initial voxel values of the region (see step “Pulmonary nodule segmentation” for details).

Running environment

All the algorithms in the experiment were implemented in MATLAB 2017a on a personal computer machine with a 2.6 GHz Intel (R) Core (TM) i7-5600 processor and 8 GB of RAM.

Proposed method

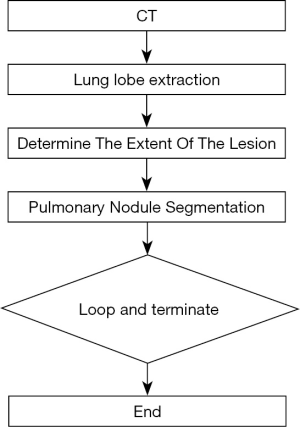
The main steps of ReGANS are: (I) extraction and optimization of lung lobes; (II) determination of the extent of lesions; (III) segmentation of pulmonary nodules; (IV) and determination and continuation (Figure 1).

Figure 1 Overview of the steps in the pretreatment approach and pulmonary nodule.

Lung lobe extraction

The goal of this step was to separate the lung lobes from the CT image and link the values of the image pixels to the medical clinical depiction. The parameters used to segment the lung lobes from the image were based on both the optimal threshold algorithm and the medical clinical description.

The gray value was converted to a CT value using information in the DICOM format file, and the abnormal point in the image was removed (6). The threshold was by an iterative algorithm (32), and the lung cavity region was extracted and recorded as IM2. Then, the threshold was calculated in IM2, combined with the location of the lobe in IM2 and other features to separate the lung lobe region C1. The boundaries of C1 were optimized using image processing techniques (33), and a new image was acquired (M3).

Determination of the extent of the lesion

Locating the pulmonary nodules is the most important step for lung nodule segmentation. A fuzzy positioning method was employed to identify the nodule range.

The probability density map IM3 was created using 0.45 as the threshold to obtain the upper limit of the lung parenchymal CT values of the current group from the graph. IM3 and the upper limit were used as the thresholds to obtain the binary image of the lung lobe (BL1). Eight rays crossing the positioned coordinate points with angles of 0°, 45°, 90°, 135°, 180°, 225°, 270°, and 315° from the horizontal were extended on BL1 until they intersected the horizontal axis. The maximum and minimum lengths of the 8 rays were removed, and the average length of the other 6 rays was calculated AvgL. The “slice_Location” in the DICOM file was used to determine the spacing of each layer to calculate the number of sheets (Ser1) that the nodule may cover. A maximum intensity projection (34) was performed on Ser1 to obtain the image IM4. A square using positioned coordinate points as the center and 2 × AvgL as the side lengths was drawn, and the square region in IM4 was defined as S1. The maximum value and the minimum values of S1 were extracted and used to perform a “bilateral filter” (35) to obtain the image (IM5). An iterative threshold algorithm was used (IM5) to obtain the threshold (T2). IM5 was binarized using the T2 threshold. The “imclose” (33) operation was subsequently performed on the image, and it was filled to obtain the lung nodule range (LNR).

Pulmonary nodule segmentation

The purpose of this step was to segment the pulmonary nodule, and it was completed after image normalization, lung lobe extraction, and lesion extension. In this step, a single image was processed, and the radiologist specified a coordinate point. The subsequent images were defined by the result of the previous image (see step D for details) with the starting image being in range of the LNR.

To calculate the range of pixel variable values within the LNR, 8 rays originating from the specified coordinate points were drawn, and the pixel values were recorded. The absolute value of the gradient value between the pixels before and after was calculated and uniquely represented by Gr. The valid data were extracted and the average (AvgS) was calculated. To calculate the center point of the pixel variation range in the LNR region, all pixel values in the were sorted from large to small, and the optimal value (EP) was extracted.

EP, AvgS, and the original image were used as inputs, and a modified region-growing method was used to obtain the putative pulmonary nodule region, PN. Based on the original Region-Growing method, our method optimized the pixel growth judgment conditions so that it could be automatically performed under the influence of EP, AvgS, and initial coordinate points. This can solve the problem of the pixel growth range in the original method needing to be manually set each time which leads to inaccurate segmentation.

Further optimization is required because of the influence of factors such as blood vessel penetration in the PN region. An “imclose” operation PN was performed to obtain a series of regions. The largest region was selected and reported as LR. Then, LR was projected onto the LNR. The region was denoted as LNI, and the regions of the LNR outside of the projection were denoted as LNO. The areas of LNI and LNO were calculated, and the average pixel values of LNI and LNO were denoted as AI and AO, and PI and PO. The following were calculated: P = PI − PO; AS = AO − AI. Using AS and P as the decision conditions, the various possible situations were analyzed, and the target area (TIM) of the image was calculated.

Loop and terminate

Because the CT was based on a series of images, the nodule segmentation continued to the next image. The average CT value of the TIM was then calculated. If it was not less than −775, and the difference in variance between this image and the previous image was less than 0.002 (the variance of the 0^thTIM was defined to be same as the 1^stTIM), the current image segmentation was considered to be valid, and the next image was processed. Otherwise, the loop was terminated. The starting coordinate point in the IM_ai step was defined as the gravity center of the TIM in IM_ai−1.

Results

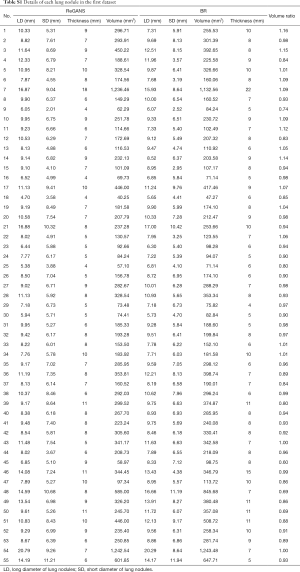
The performance of the newly developed ReGANS method was evaluated and compared with Snake, SBGFRLS, and level-set method, taking two types of radiologist’s segmentation results as a benchmark. The lesion boundary delineated by radiologists was defined as the boundary range (BR), while the precise range (PR) was BR without blood vessels and bronchi. The performance of the ReGANS was evaluated in aspects of accuracy, speed, and robustness. In addition, detailed information on the pulmonary nodules used in the first dataset was also recorded (Table S1, supplementary material).

Table S1 Details of each lung nodule in the first dataset
Full table

The accuracy and robustness of the ReGANS were evaluated by PRI, GCE, and VoI (19,36). Using the MATLAB runtime environment, the “compare_segmentations.m” toolkit was downloaded to perform calculations (https://www.dssz.com/778476.html).

Accuracy

The planar segmentation results of the four algorithms were compared based on the second dataset. The accuracies of these algorithms are shown in Table 2.

Table 2 Accuracy of each segmentation result
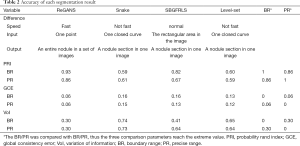
Full table

The average PRI of ReGANS, when compared to BR, was 0.93 (95% CI, 0.90–0.96), while that of the other three algorithms was lower (0.59–0.82), which indicated that ReGANS could get more accurate results close to BR. Meanwhile, the average GCE between ReGANS and BR was 0.058 (95% CI, 0.05–0.07), which suggested that the global error of ReGANS was negligible. Consistently, the average VoI between ReGANS and BR was 0.30 (95% CI, 0.26–0.34). The average GCE and VoI ofReGANS were significantly lower than those of the other three algorithms (for all comparison, P<0.0001). The average PRI, GCE, and VoI between the ReGANS and PR were 0.86 (95% CI, 0.84–0.88), 0.06 (95% CI, 0.052–0.068), and 0.30 (95% CI, 0.27–0.33), respectively. These results indicate that the segmentation performance of the ReGANS was comparable to that of PR.

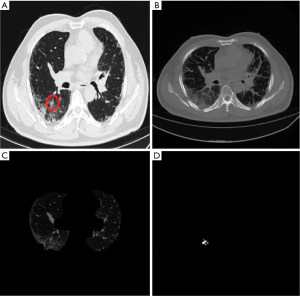
The supero-inferior coverage difference between the PR and ReGANS in each sample was compared; the radiologist diagnosed 166 images, 28 of the ReGANS results were not in the radiologist's diagnosis, and two correct results were not calculated. The result showed that the error and loss rate of the range of tuberculosis detected by the ReGANS was less than 18% (Figure 2A). Most of the missing images were terminal in each sample. The CT values of the nodule range were close to the lung parenchyma, causing it to be ignored by the ReGANS (Figure 2B).

Figure 2 Algorithm detection results compared with actual nodule coverage. In (A), the blue area represents the intersection between ReGANS and the manual annotation superoinferiorly; the yellow area represents the images neglected by ReGANS; the black area represents extra images calculated by ReGANS; I indicates the nodules in this set of data that have no other tissue interference; II represents one blood vessel/bronchus passing through the lung nodules; III represents multiple blood vessels/bronchi passing through the lung nodules. (B) represents a missing image due to the CT value of the lung nodule area in the image being low. (C) represents an extremely irregular pulmonary nodule and depicts the results of the ReGANS algorithm. (D) shows a pulmonary nodule with blood vessels passing through and depicts the results of segmentation by the ReGANS method.

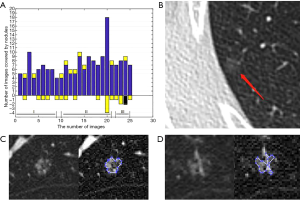
The performance of the ReGANS on special types of pulmonary nodules was also adequate. The ReGANS could segment lung nodules with special signs, like the vacuole sign (Figure 2C). For special lung nodules with blood vessels or bronchial passages, the ReGANS could also be effectively segmented, although the complete effective area of the pulmonary nodules is not fully depicted in Figure 2D. Collectively, the ReGANS exhibited a better accuracy than the other algorithms.

Speed

The segmentation time of each algorithm was recorded as the number of images of lung nodules in each group of data ranging from 4–22. Eight images (average) were used to calculate the overall segmentation time. The average segmentation time of a single CT image was 0.83 s (95% CI, 0.829–0.840) and segmentation of all the lung nodule images took 6.64 s (Table 3). The average segmentation times of the Snake, SBGFRLS, and level-set methods for a single image were 13.04, 2.42, and 19.02 s, respectively. The radiologists’ manual segmentation time was 60 s, and thus, a minimum of 480 s (8 min) was required to process these images.

Table 3 Time of segmentation of each method
Full table

The time required to segment the image with the ReGANS was generally consistent. Images with special types of nodules did not significantly increase the time required. As shown in Figure 2D, the time required by the ReGANS was only 0.92 s. Thus, the speed of the ReGANS was significantly higher than those of the other algorithms.

Robustness

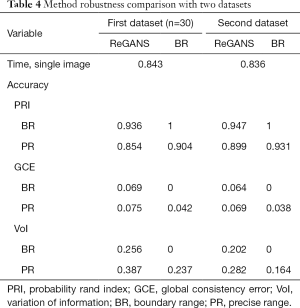
ReGANS was also used to split 30 sets of images in the first dataset and images in the third dataset. The accuracy and speed of the ReGANS were evaluated for those two datasets, as shown in Table 4.

Table 4 Method robustness comparison with two datasets
Full table

At the same time, the serial number of the lung nodule image in a set of case images calculated by REGAN was also recorded and compared with the diagnostic results of the radiologist. In the 30 images in the first dataset, the radiologist diagnosed 241 images, 17 of the ReGANS results were not in the radiologist's diagnosis, and 12 correct results were not calculated. In the 30 images in the third dataset, the radiologist diagnosed 234 images, 14 of the ReGANS results were not in the radiologist's diagnosis, and 9 correct results were not calculated. The total error rate was 10.95%

Further inspection

To further evaluate the segmentation accuracy of the ReGANS method in other diseases of the lung. We collected some CT images of pulmonary fibrosis for segmentation experiments. The segmentation results are shown in the appendix.

Discussion

Most currently reported algorithms are not satisfactory for clinical application. First, automatic segmentation operations usually must be performed on 5–10 images, sometimes 20, and the time spent for published algorithms is several minutes (29-31). Second, other methods have many complicated pre-processing steps and cumbersome manual operations (37), including determining approximate ranges, building similar shapes, and enhancing image contrast. Moreover, in some algorithms, iterative analysis is required, and professional training is necessary. The automatic segmentation algorithms require a substantial amount of data and manual targets to establish models through algorithms. These models are affected by data volume, data classification, and artificial results. Lastly, in most cases, the reported algorithms cannot process a set of images as a single sample. In other words, the supero-inferior images of a patient cannot be processed automatically. A few researchers have developed automatic supero-inferior algorithms, but at a low speed with more than 10 min needed.

ReGANS requires only 6–8 s, even for complicated lung nodules. Only one-click operation is required for the ReGANS, and the radiologist does not need to pre-process the images and select the pulmonary nodule one image at a time. ReGANS is a very simple operation that offers a radiologist with a continuous feature image of a pulmonary nodule quickly and accurately. This can effectively help radiologists by providing them with reliable diagnostic information. To a certain extent, they are freed from a whole day of tedious work.

Segmentation algorithms based on machine learning or deep learning do have significant advantages. A mature model that completes training can also quickly and accurately segment the lesion area in practical applications. In some cases where hardware devices are better, they can even do segmentation faster than ReGANS, but, limited by the design of the model itself, the quality of the training image directly affects the capabilities of the model. With high speed and accuracy, ReGANS can provide high-quality annotation images for model training and effectively compress the pre-preparation time.

ReGANS also has its limitations. The threshold calculation process for image binarization is a bit conservative, which leads to the missing of terminal images when segmenting. The automatic boundary calculation of the lung nodule starts from an initial manual point. In some extremely complicated situations, such as multiple blood vessels passing through the lung nodules, to avoid the blockage of blood vessels and other tissues, the segmentation of the lung nodules will always leave some areas behind. In addition, determining the extent of pulmonary nodules for radiologists is only part of the diagnostic process, and subsequent analysis of signs such as lobulation, bronchus sign, and pleural indentation requires a more accurate diagnosis. This requires the subsequent segmentation method to be able to not only accurately determine the lesion area, but also to identify each sign. What is more, the segmentation results of pulmonary fibrosis also reflect the limitations of ReGANS. Although the “maximum intensity projection” method applied in ReGANS can define the lesion area of the lung nodule image well, it can also cause overlapping features of multiple lesions in some more complex images, which instead interferes with the algorithm’s determination of the suspected area of the lesion and also interferes with the “segmentation threshold calculation” and “segmentation result optimization” in the later stages of the algorithm.

An evolved method is then required to convert the image information into medical clinical description, so as to identify the lesion signs from the perspective of image semantics, and finally, provide more accurate diagnostic information for radiologists. This is also the future research direction of ReGANS.

Conclusions

The experiments showed that this semi-automatic lung nodule segmentation method can accurately and quickly segment all the lung nodule images in a set of CT data while also preserving the original characteristics of lesions. It can effectively assist the radiologist’s diagnosis and provide reliable training data for intelligent algorithms.

Supplementary

Proposed method

The main steps of the ReGANS are depicted in Figure S1. In the first step, the gray values of the CT image are converted into CT values, and the pulmonary lobe is segmented and optimized. The maximum projection area of the pulmonary nodules on the horizontal plane is then determined, and the pulmonary nodules are subsequently segmented using the projection area. Finally, the parameters are calculated to decide whether to continue to the next image.

Figure S1 Segmentation results of ReGANS in CT images of pulmonary fibrosis lesions.

Lung lobe extraction

The goal of this step was to separate the lung lobes from the CT image and link the values of the image pixels to the medical clinical depiction. The parameters used to segment the lung lobes from the image were based on both the optimal threshold algorithm and the medical clinical description.

Step 1: image normalization

DICOM is a standard format for the communication and management of medical imaging information and related data. The “RescaleSlope” and “RescaleIntercept” parameters were used to convert the calculation of the gray value back to the CT values using the following formula:

HU= pixel_value × RescaleSlope + RescaleIntercept [1]

where “RescaleSlope” and “RescaleIntercept” are the DICOM tags that specify the linear transformation for the pixels to be converted from their stored on-disk representation to their in-memory representation.

Extreme data were subsequently removed. To prevent interference from extreme data points such as those resulting from metal objects in the image, highlighted pixels in the image were removed. The full graph histogram was obtained, using 0.0039 as the interval, because the abnormal values were generally in the last few intervals. The pixel value distribution of each interval from the back to the previous time was analyzed, and extreme values were eliminated using thresholds. The processed images (denoted IM1) were used for further analyses.

Step 2: extraction of the lung lobes

This step involves pulmonary cavity extraction and lung lobe extraction. Pulmonary cavity extraction is necessary for lung lobe extraction because interference of invalid information, including machine shadows and the background, must be removed from the image. There are typically few background shadows, and their CT values are usually consistent. Here, an Iterative thresholding algorithm was used. The zero gray values were not used to obtain the threshold (T) of the image, which allowed it to be binarized (the zero values were removed, and the image was processed by the iterative algorithm to obtain the threshold for the pulmonary cavity extraction). The boundary was defined, holes inside the regions were filled, and the largest closed area yielding the novel image (IM2) was obtained. This was used for further lung lobe extraction. IM1 was binarized with T to obtain the binary image BIM1. The following formula was used: C1 = BIM1 − IM2. The number of closed areas of C1 was calculated and denoted H1. If H1 > 2, the three largest closed areas were extracted, and the left and right areas on the X-axis were selected as lung lobes. If H1 = 2, the centers were labeled as (x1, y1) and (x2, y2). If |x1−x2|>|y1−y2|, both areas were retained. Otherwise, the larger area was retained as a merged lung lobe. If H1 = 1, the area was identified as a merged lung lobe.

Step 3: boundary optimization

The boundaries of the lungs were optimized to facilitate the extraction. An ellipse with 10 and 30 pixels as the minor and major axes, respectively, was created to accommodate the shape of the lung. The left and right lungs were separated into two independent images. An “imopen” operation on the two images was performed with the previous ellipse (if the left and right lungs in the previously extracted lung lobe area were connected at the top, the image erosion algorithm was used to separate and restore them through the expansion algorithm). The processed images were subsequently combined into a new binary image (BIM2) representing the extracted lung lobes, and the following calculation was performed: IM3 = BIM2 − IM1.

Determination of the extent of the lesion

Locating the pulmonary nodules is the most crucial step for lung nodule segmentation. Most nodules grow in approximate symmetry. A fuzzy positioning method was employed to identify the nodule.

First, a histogram of IM4was plotted. The probability density map was created using 0.45 as the threshold to obtain the upper limit of the lung parenchymal CT values of the current group from the graph. IM4and the upper limit were used as the thresholds to obtain the binary image of the lung lobe (BL1). Eight rays crossing the positioned coordinate points with angles of 0°, 90°, 45°, 135°, 180°, 225°, 270°, and 315° from the horizontal were extended on BL1 until they intersected the horizontal axis. The maximum and minimum lengths of the 8 rays were removed, and the average length of the other 6 rays was calculated as AvgL. The DICOM image information “slice_Location” was used to determine the spacing of each layer (the slice location values of the current image (SL1) and the previous image (SL2) were obtained by parsing the DICOM file) to calculate the number of sheets that the nodule may cover (AvgL/(|SL1−SL2|)). The maximum area of the nodules was also in the middle. To avoid projecting excessive sheets, if the estimated image number exceeded the threshold (5), the number of sheets was reduced to the threshold as Series 1 (Ser1). A maximum intensity projection (35) was performed on Ser1 to obtain an image, IM3. The previous “lung lobe extraction” step process, M1, was used. A square using positioned coordinate points as the center and 2 × AvgL as the side lengths was drawn, and the square region was defined as S1. The maximum value and the minimum values in S1 were extracted and used to perform a “bilateral filter” (36) to obtain the image (IM5). An iterative threshold algorithm was used on IM5 to obtain the threshold (T2). IM5 was binarized using a threshold T2. The “imclose” operation was subsequently performed on the image, and it was filled to obtain the lung nodule range (LNR).

Pulmonary nodule segmentation

After the image normalization, lung lobe extraction, and lesion extension, the purpose of this step was to segment the pulmonary nodule. In this step, a single image was processed, and the radiologist specified a coordinate point. The subsequent images were defined by the result of the previous image (see step D for details). The starting image was in the range of the LNR.

• Eight rays originating from the specified coordinate points were drawn, and the pixel values were recorded.
• The unique absolute gradient values between the pixels on these 8 lines were calculated and denoted as Gr.
• The largest 20% of all gradients were extracted and denoted as S.
• If the number of S was less than 4, Gr was used as S.
• The maximum of S was removed, and the remaining average of S was calculated and denoted as AvgS.
• If RA was less than 0.031 and S was greater than 6, the average of the largest 6 values of S replaced AvgS.
• If AvgS was greater than 0.1, AvgS was replaced with 0.08.
• All the pixel values of the LNR were sorted, and the pixel values between 50% and 85% were extracted and denoted as EP.
• The 3rd quartile of EP was extracted.
• EP, AvgS, and IM1 were used as inputs, and a modified region-growing method was used to obtain the putative pulmonary nodule region, PN.
• PN was optimized. A closing operation on PN was performed to obtain a series of regions. The largest region was selected and denoted as LR.
• LR was projected onto the LNR. The region was denoted as LNI, and the regions of the LNR outside of the projection were denoted as LNO.
• The area of LNI and LNO were calculated, and the average pixel values of LNI and LNO were denoted as AI and AO, and PI and PO. The following were calculated: P=PI-PO, AS=AO/AI.
• If AS was greater than 0.1 and P was greater than 0 LNO was iterated to obtain a threshold and omit pixels larger than the threshold in PN as the target region of this image (TIM); if AS was in the 0.1–0.3 range, and P was less than 0, an open operation on PN was performed, and the TIM was obtained. If AS was greater than 0.3 and P was less than 0, PN was projected onto the LNR, and the TIM was obtained. For the other conditions, PN was defined as the TIM.

Loop and terminate

Because the CT was based on a series of images, the nodule segmentation continued to the next image. The average CT value of the TIM was then calculated. If it was not less than −775, and the difference in variance between this image and the previous image was less than 0.002 (the variance of the 0^th TIM was defined to be same as the 1^st TIM), the current image segmentation was considered to be valid, and the next image was processed. Otherwise, the loop was terminated. The starting coordinate point in the IM_ai step was defined as the gravity center of the TIM in IM_ai-1.

Acknowledgments

Funding: The Project was supported by the National Key Research and Development Program of China (Grant No. 2016YFC0901903); the Shanghai Municipal Health Commission (Grant No. 2018ZHYL0104); the Shanghai Committee of Science and Technology, China (Grant No. 18511102700).

Footnote

Conflicts of Interest: The authors have no conflicts of interest to declare.

Ethical Statement: The study design was approved by the Shanghai University of Medicine and the Health Sciences Ethics Review Board. The need for informed consent was waived.

References

1. Siegel RL, Miller KD, Jemal A. Cancer statistics, 2019. CA Cancer J Clin 2019;69:7-34. [Crossref] [PubMed]
2. Bray F, Ferlay J, Soerjomataram I, Siegel RL, Torre LA, Jemal A. Global cancer statistics 2018: GLOBOCAN estimates of incidence and mortality worldwide for 36 cancers in 185 countries. CA Cancer J Clin 2018;68:394-424. [Crossref] [PubMed]
3. Aberle DR, Berg CD, Black WC, Church TR, Fagerstrom RM, Galen B, et al. The National Lung Screening Trial: overview and study design. Radiology 2011;258:243-53. [Crossref] [PubMed]
4. Hansell DM, Bankier AA, MacMahon H, McLoud TC, Muller NL, Remy J. Fleischner Society: glossary of terms for thoracic imaging. Radiology 2008;246:697-722. [Crossref] [PubMed]
5. Raad RA, Suh J, Harari S, Naidich DP, Shiau M, Ko JP. Nodule characterization: subsolid nodules. Radiol Clin North Am 2014;52:47-67. [Crossref] [PubMed]
6. Shin HB, Sheen H, Lee HY, Kang J, Yoon DK, Suh TS. Digital Imaging and Communications in Medicine (DICOM) information conversion procedure for SUV calculation of PET scanners with different DICOM header information. Phys Med 2017;44:243-8. [Crossref] [PubMed]
7. Zhao Y, de Bock GH, Vliegenthart R, van Klaveren RJ, Wang Y, Bogoni L, de Jong PA, Mali WP, van Ooijen PM, Oudkerk M. Performance of computer-aided detection of pulmonary nodules in low-dose CT: comparison with double reading by nodule volume. Eur Radiol 2012;22:2076-84. [Crossref] [PubMed]
8. Jin S, Zhang B, Zhang L, Li S, Li S, Li P. Lung nodules assessment in ultra-low-dose CT with iterative reconstruction compared to conventional dose CT. Quant Imaging Med Surg 2018;8:480-90. [Crossref] [PubMed]
9. Mao L, Chen H, Liang M, Li K, Gao J, Qin P, Ding X, Li X, Liu X. Quantitative radiomic model for predicting malignancy of small solid pulmonary nodules detected by low-dose CT screening. Quant Imaging Med Surg 2019;9:263-72. [Crossref] [PubMed]
10. Theilig D, Doellinger F, Kuhnigk JM, Temmesfeld-Wollbrueck B, Huebner RH, Schreiter N, Poellinger A. Pulmonary lymphangioleiomyomatosis: analysis of disease manifestation by region-based quantification of lung parenchyma. Eur J Radiol 2015;84:732-7. [Crossref] [PubMed]
11. Rausch SM, Martin C, Bornemann PB, Uhlig S, Wall WA. Material model of lung parenchyma based on living precision-cut lung slice testing. J Mech Behav Biomed Mater 2011;4:583-92. [Crossref] [PubMed]
12. Perez-Rovira A, Kuo W, Petersen J, Tiddens HA, de Bruijne M. Automatic airway-artery analysis on lung CT to quantify airway wall thickening and bronchiectasis. Med Phys 2016;43:5736. [Crossref] [PubMed]
13. Mumcuoğlu EU, Long FR, Castile RG, Gurcan MN. Image analysis for cystic fibrosis: computer-assisted airway wall and vessel measurements from low-dose, limited scan lung CT images. J Digit Imaging 2013;26:82-96. [Crossref] [PubMed]
14. Wang B, Tian X, Wang Q, Yang Y, Xie H, Zhang S, Gu L. Pulmonary nodule detection in CT images based on shape constraint CV model. Med Phys 2015;42:1241-54. [Crossref] [PubMed]
15. McWilliams A, Tammemagi MC, Mayo JR, Roberts H, Liu G, Soghrati K, Yasufuku K, Martel S, Laberge F, Gingras M, Atkar-Khattra S, Berg CD, Evans K, Finley R, Yee J, English J, Nasute P, Goffin J, Puksa S, Stewart L, Tsai S, Johnston MR, Manos D, Nicholas G, Goss GD, Seely JM, Amjadi K, Tremblay A, Burrowes P, MacEachern P, Bhatia R, Tsao MS, Lam S. Probability of cancer in pulmonary nodules detected on first screening CT. N Engl J Med 2013;369:910-9. [Crossref] [PubMed]
16. Cavalcanti PG, Shirani S, Scharcanski J, Fong C, Meng J, Castelli J, Koff D. Lung nodule segmentation in chest computed tomography using a novel background estimation method. Quant Imaging Med Surg 2016;6:16-24. [PubMed]
17. Shen S, Bui AAT, Cong J, Hsu W. An automated lung segmentation approach using bidirectional chain codes to improve nodule detection accuracy. Comput Biol Med 2015;57:139-49. [Crossref] [PubMed]
18. Lee SLA, Kouzani AZ, Hu EJ. Automated detection of lung nodules in computed tomography images: a review. Machine Vision Applications 2012;23:151-63. [Crossref]
19. Jiang X, Marti C, Irniger C, Bunke H. Distance measures for image segmentation evaluation. Eur J Applied Signal Processing 2006;(35909).
20. Hu S, Hoffman EA, Reinhardt JM. Automatic lung segmentation for accurate quantitation of volumetric X-ray CT images. IEEE Trans Med Imaging 2001;20:490-8. [Crossref] [PubMed]
21. Brown MS, McNitt-Gray MF, Mankovich NJ, Goldin JG, Hiller J, Wilson LS, Aberle DR. Method for segmenting chest CT image data using an anatomical model: Preliminary results. IEEE Trans Med Imaging 1997;16:828-39. [Crossref] [PubMed]
22. Wong LM, Shi L, Xiao F, Griffith JF. Fully automated segmentation of wrist bones on T2-weighted fat-suppressed MR images in early rheumatoid arthritis. Quant Imaging Med Surg 2019;9:579-89. [Crossref] [PubMed]
23. Zhao L, Jia K. Multiscale CNNs for Brain Tumor Segmentation and Diagnosis. Comput Math Methods Med 2016;2016:8356294. [Crossref] [PubMed]
24. Zhu Y, Tan Y, Hua Y, Zhang G, Zhang J. Automatic Segmentation of Ground-Glass Opacities in Lung CT Images by Using Markov Random Field-Based Algorithms. J Digit Imaging 2012;25:409-22. [Crossref] [PubMed]
25. Zhou S, Cheng Y, Tamura S. Automated lung segmentation and smoothing techniques for inclusion of juxtapleural nodules and pulmonary vessels on chest CT images. Biomed Signal Processing Control 2014;13:62-70. [Crossref]
26. Messay T, Hardie RC, Rogers SK. A new computationally efficient CAD system for pulmonary nodule detection in CT imagery. Med Image Anal 2010;14:390-406. [Crossref] [PubMed]
27. Lin J, Peng B, Li T, Chen Q. A Learning-Based Framework for Image Segmentation Evaluation. In: International Conference on Intelligent Networking & Collaborative Systems; 2013 2013: IEEE Computer Society; 2013:691-6.
28. Bellare M, Namprempre C, Neven G. Security Proofs for Identity-Based Identification and Signature Schemes. J Cryptol 2009;22:1-61. [Crossref]
29. Kass M, Witkin A, Terzopoulos D. Snakes: Active Contour Models. Int J Computer Vision 1987;1:321-31. [Crossref]
30. Zhang K, Zhang L, Song H, Zhou W. Active contours with selective local or global segmentation: A new formulation and level set method. Image Vision Computing 2010;28:668-76. [Crossref]
31. Osher SP, Fedkiw R. Level Set Methods and Dynamic Implicit Surfaces. In: Applied Mathematical Sciences 2004:xiv+273.
32. Perez A, Gonzalez RC. An Iterative Thresholding Algorithm for Image Segmentation. IEEE Trans Pattern Anal Mach Intell 1987;9:742-51. [Crossref] [PubMed]
33. Gonzalez RC, Woods RE. Digital Image Processing. 1977.
34. Sato Y, Shiraga N, Nakajima S, Tamura S, Kikinis R. Local maximum intensity projection (LMIP): a new rendering method for vascular visualization. J Comput Assist Tomogr 1998;22:912-7. [Crossref] [PubMed]
35. Morillas S, Gregori V, Sapena A. Fuzzy Bilateral Filtering for Color Images. Sensors (Basel) 2011;11:3205-13. [Crossref] [PubMed]
36. Monteiro FC, Campilho AC. Performance evaluation of image segmentation. In: Campilho A, Kamel M. editors. ICIAR 2006. Lecture Notes Computer Science 2006:248-59.
37. Li B, Chen Q, Peng G, Guo Y, Chen K, Tian L, et al. Segmentation of pulmonary nodules using adaptive local region energy with probability density function-based similarity distance and multi-features clustering. Biomed Eng Online 2016;15:49. [Crossref] [PubMed]