Coil combination using linear deconvolution in k-space for phase imaging
Introduction
Magnetic resonance imaging (MRI) has been widely used in clinical medicine owing to its advantages of high spatial resolution, lack of ionizing radiation, high tissue resolution, arbitrary slice scanning, and multi-parameter imaging (1-4). Although the detected MR signal is complex-valued, the remarkable development of magnitude information has been accompanied by a marked increase in application over the last 40 years (5-7). In fact, the phase information can provide much higher gray-white matter contrast than the corresponding magnitude, and contains unique information regarding deoxyhemoglobin, iron, myelin, and tissue microstructure (8-11). Nevertheless, the clinical application of phase information has been handicapped by its poor signal-to-noise ratio (SNR) and limited spatial resolution in low-field-strength MRI (3 Tesla) and its accompanying accentuated susceptibility effects (12) make the clinical use of phase information feasible.
In high-field MRI (>1.0T), the k-space signal is generally acquired with a set of coil-array to improve the SNR and provide the necessary information to carry out accelerated parallel imaging (13-16). The phase received by each coil involves tissue, coil, and background phases caused by main field inhomogeneities and shimming field (17,18). Consequently, the optimal coil combination and background field removal operation are necessary to obtain the tissue phase in most phase applications, such as in susceptibility-weighted imaging (SWI) (19,20), and quantitative susceptibility mapping (QSM) (21-24). Although various coil combination methods have been developed to obtain a phase image over the last decade, none has been adopted as a standard method in clinical application.
Traditional methods apply phase unwrapping and background phase removal for each coil as the first step, and then combine all coil phase images weighted by the square of magnitudes (13). The magnitude image suffers from amplified noise and artifacts, which could be further propagated in the magnitude-weighted phase image in the scenario of accelerated parallel imaging. Additionally, the correlation between coils is ignored in these methods. Thunberg et al. (25) and Lu et al. (26) independently stated that phase variance can be reduced when including coil correlation in the sensitivity encoding for fast MRI (SENSE) reconstruction at non-accelerated scenarios. The auto-calibrated SENSE (mSENSE) was later extended on the complex image (27). Walsh et al. replaced the magnitude with coil sensitivity as the combination weights (28). Chen et al. applied a Gaussian low-pass smoothing filter for sensitivity phase estimation based on the maximization of signal-to-noise ratio in phase images (29). The accuracy of these SENSE reconstruction methods heavily depends on the coil sensitivity that is often unavailable in clinical applications.
In the absence of accurate coil sensitivity, the constant offsets-based multi-channel phase combination (MCPC-C) (9) method aligns all coil phase images by subtracting channel-dependent phase offsets before the magnitude-weighted combination. The channel-dependent phase offsets are estimated from the mean phase value in a matching region of interest, such as the center of the field of view (FOV) (30) or a place with maximum magnitude (7). Such methods hypothesize that phase offsets are consistent over entire the FOV, which is not true with UHF. The method of reference (31) generates a virtual coil by using the MCPC-C method, and then combines the multiple coils using the inverse covariance method. However, the robustness of the virtual coil approach with different coil designs and field strengths remains to be investigated.
All the above-mentioned methods that combine coil data in the image space are good at optimizing the final image SNR (32,33). Despite this, such image-space-based solutions can be computationally intensive, especially for high channel count coil arrays, as the phase wrapping needs to be addressed for each individual coil before combinations (34,35).
In this study, we propose a k-space-based method for coil combination by using linear deconvolution, abbreviated as CODEC. Considering that the signal received by each coil is the result of two-dimensional convolution in the k-space between the proton spin intensity and coil sensitivity, the proposed method reformulates the coil combination as a de-convolutional problem in k-space where the coil combination weights are estimated with the acquired auto-calibrating signals (ACS) near the center of k-space data. Experimental results of phantom and in vivo brain images are provided to demonstrate the performance of the proposed method compared with the magnitude-weighted methods.
Problem formulation
Ignoring the off-resonance and the noise, the signal acquired from the l-th channel on coordinate (kx,ky) denoted as sl(kx,ky) can be represented as:
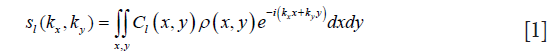
where Cl(x,y) is the coil sensitivity of l-th coil on location (x,y), l=1,2,...L, L the number of coils in the array, and ρ(x,y) the density of proton spin in spatial location (x,y). Most magnitude image reconstruction is performed using the inverse covariance method of Roemer (13), named the sum-of-squares (SOS) method:

The phase acquired from the l-th coil, θl, can be represented as

where ΔB0 is the local bias of magnetic field caused by either imperfect shimming or susceptibility of tissue, TE is echo time and θRX,l represents the space-varying coil phase. Since the phase is obtained by arc-tangent function, the phase is wrapped into (−π,π] and Φ() in Eq. [3] represents the phase wrapping operation, which is defined as the following:
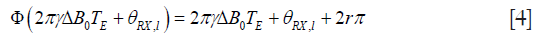
where r is an integer satisfying  .
.
The phase can accurately depict the susceptibility of tissue under perfect shimming. Reconstructing the absolute phase of tissue generally involves coil combination, phase unwrapping, and background removal. In terms of coil combination, magnitude-weighted (13) and MCPC-C (9) methods are the representative state-of-the-art approaches that will be detailed in the following subsections.
Magnitude-weighted methods
The noise of the phase image estimated by two-point measure methods (36,37) is inversely proportional to the magnitude Il and proportional to the standard deviation of magnitude image: σmag,

where 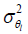 is the variance of the noise in the l-th phase image. Consequently, magnitude-weighted (MW) method chooses the square of magnitude as the combination weight (13) to maximize the SNR of the final phase image. The combined phase, denoted as θwm, can be represented as the following:
is the variance of the noise in the l-th phase image. Consequently, magnitude-weighted (MW) method chooses the square of magnitude as the combination weight (13) to maximize the SNR of the final phase image. The combined phase, denoted as θwm, can be represented as the following:

MCPC-C
In the MCPC-C approach, channel offsets which are assumed to be constant throughout the image, are estimated from the phase at a single voxel location or over a region where signals can be received from all coils. The scalar channel offset 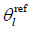 is subtracted from each channel l, setting the phase of all channels to zero at the point of correction. The weighted mean phase over all channels is calculated as follows (9):
is subtracted from each channel l, setting the phase of all channels to zero at the point of correction. The weighted mean phase over all channels is calculated as follows (9):

where scalar channel offset 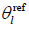 can be estimated with the mean phase of the center pixels:
can be estimated with the mean phase of the center pixels:

where x∊Ω region Ω locates in the center of FOV.
Both the MW and MCPC-C methods combine all coil phases by assigning a magnitude depending on the weight of each pixel, which can produce the optimal phase image under non-accelerated scenarios. Nonetheless, the magnitude image reconstructed by parallel imaging algorithms with accelerated sampling data can be contaminated with aliasing artifacts and the amplified noise in coil combination. To circumvent this dilemma, we propose a k-space-based coil combination method that computes the optimal coil k-space combination weights by utilizing the Fourier transforms of coil sensitivity and the ACS. In this subsection, we first reformulate the coil combination as a convolution problem and then detail the process of the proposed CODEC method.
Coil combination in k-space
The received image from the l-th coil, Il, is the multiplication of proton density ρ and coil sensitivity Cl:

Applying the fast Fourier transformation (FFT) on both sides of Eq. [9], the multiplication in the right hand of Eq. [9] changes into a convolutional operation based on the convolutional theory of the Fourier transform,

The proton density can be approximated as a linear combination of all coil images:

where μl(x,y) is the combined weight of the l-th coil on the pixel location (x,y). The combination weight varies according to the spatial location. Resorting to the convolutional and linear properties of the Fourier transform, the k-space signal of proton density can be estimated with a linear combination among coils after the 2D convolution between the frequency spectrum of coil sensitivity and coil combination weight:
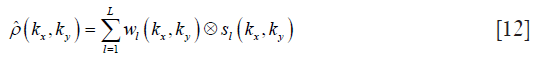
where wl denotes the coil combination weight on k-space, and it is the Fourier transform of μl.
As shown in Eq. [11], the optimal coil combination weight μl is directly proportional to the coil sensitivity (38):

Therefore, μl can be assumed to change slowly just as coil sensitivity does. Thus, most energy of wl concentrates on its central region. The k-space-based parallel imaging methods that utilize a small interpolation window to reconstruct the missing k-space are also based on the same assumption such as SMASH (39) and GRAPPA (40). Consequently, the real k-space signal of the scanned tissue can be approximated as a linear combination of coils after the convolution between the windowed frequency spectrum of coil sensitivity and coil image:
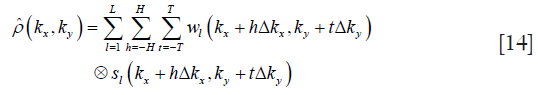
where h and t are the indexes of 2D convolution, and H and T are the sizes of convolutional kernel along the frequency encoding (FE) and phase encoding (PE), respectively. Substituting Eq. [14] into Eq. [10] results in the following:

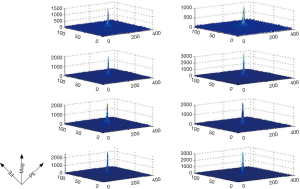
Due to the nature of slow spatial varying, the energy of the spectrum of coil sensitivity mostly concentrates on the central low-frequency region, as shown in Figure 1. Therefore, the full k-space of coil sensitivity can be approximately truncated to keep the central region in Eq. [15]:

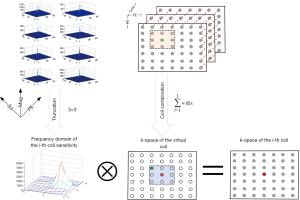
where (•)∏ represents the truncation operator. Eq. [16] shows that the coil combination weight in the frequency domain can be estimated by using the deconvolution between coil sensitivity and ACS data, as shown in Figure 2. Then, the k-space signal can be computed using Eq. [16], and finally, both phase and magnitude can be obtained by using inverse FFT.
Algorithm
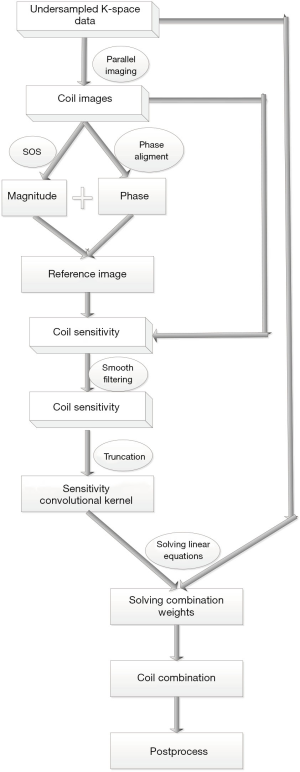
The proposed method combines coil in k-space where the combination weights are estimated in a deconvolution form. Figure 3 illustrates the process of phase combination from multi-channel data. The proposed method first estimates a reference complex image that has a uniform sensitivity for each coil. Then, the computation of the coil combination weights is reformulated as solving a linear equation. The following subsection details the coil estimation and coil combination in k-space.
Coil sensitivity estimation
SENSE utilizes the magnitude image as the reference image, which ignores the phase information. In this study, the magnitude and phase are estimated separately. Firstly, a magnitude image is obtained using the SOS method:

Meanwhile, the reference phase θvir is computed withEqs. [7] and [8]. Then, by combining the magnitude and phase, coil sensitivity can be estimated as follows:

The coil sensitivity may contain noise which can be smoothed using a second-order polynomial filter. Finally, the size of the convolutional kernel is determined in the center of the frequency domain of the coil sensitivity.
Constructing linear equations
As shown in Figure 2, all coil k-space data are convolved with a combination kernel to yield the virtual coil k-space data. Hence, each point of coil k-space data can be viewed as the convolution of the virtual k-space data and the truncated frequency of coil sensitivity, which is a forward convolutional model. Based on this model, coil combination weight can be solved by constructing a set of linear equations with received ACS and coil sensitivity.
Taking the red k-space point from the i-th coil in Figure 2 as an example, the process of constructing the convolutional k-space model is described as follows. For simplicity, the data points in the combination weight kernel are indexed from 1 to M, ordering from left to right and from top to bottom. Similarly, the data points in the coil sensitivity kernel are indexed from 1 to N. M and N are the amounts of data points in combinational weight kernels and coil sensitivity kernels, respectively.
Since the multi-channel coil k-space data are combined into one virtual coil k-space, the value of green point (X) in Figure 2 can be represented as follows:
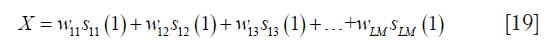
where wij is the coil k-space combination weight of the i-th coil on location j, and sij(n) represents the i-th coil on location j to obtain the point on location n in the convolutional kernel. Here, the green point, being the first point in the convolutional kernel, is written as sij(1). The combined data can be viewed as k-space data received by a virtual coil that has a uniform distribution on the entire FOV. Consequently, the k-space data received by each coil can be considered as the convolutional result of the virtual coil k-space data and frequency kernel of coil sensitivity. The green point in Figure 2 belongs to the first point in the frequency kernel of coil sensitivity. Thus, the combination weights of the green point (Y) can be written as follows:
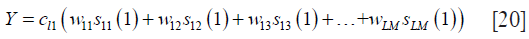
where cln is the frequency kernel weight of coil sensitivity of l-th coil on location n. Therefore, the k-space data point 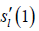 of the l-th coil can be reconstructed as follows:
of the l-th coil can be reconstructed as follows:
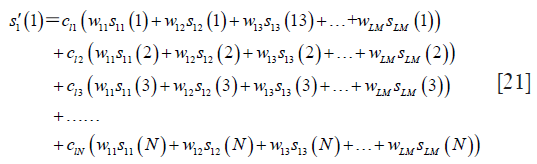
For legibility, 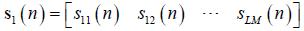 let, and
let, and 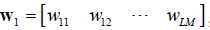 , and Eq. [21] can be rewritten as follows:
, and Eq. [21] can be rewritten as follows:
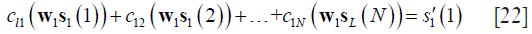
Extracting out w1 from the left hand of Eq. [22], one can obtain the following linear equation:
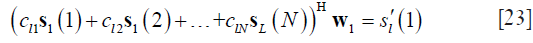
In the above equation, all variables are known except the coil combination weight. By sliding the combination kernel along the PE and FE directions, one can gather one over-determined linear equation to solve the coil combination weights. Though one set of coil sensitivity is used in Eq. [23], more equations can be obtained by using all the coil data to obtain a more robust solution. Finally, the calibration can be simply written as follows:

where matrix A is composed of coil sensitivity and coil k-space data, vector w represents the combination weights, and vector b is composed of the fitted coil k-space data. A closed-form solution of combination weights can be obtained as follows:

With the combination weights obtained, the combined coil k-space data can be computed as follows:

In this study, a 7×7 convolutional kernel is used; thus, the combined coil k-space can be computed as follows:
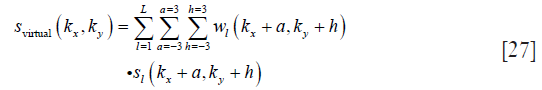
where svirtual(kx,ky) is the combined coil k-space data on coordinate (kx,ky), and a and h define the size of the convolutional kernel, respectively.
By applying IFFT on svirtual, the phase θvirtual=∠(IFFT(svirtual))and magnitude |IFFT(svirtual)| can be obtained simultaneously.
Methods
Data acquisition
The performance of the proposed method was confirmed using two scanned datasets. A phantom dataset was produced by using MagphanVR phantom (Phantom Laboratory, Salem, NY, USA) and an axial brain dataset was acquired on a 3.0T Discovery MR750 (GE Healthcare, Waukesha, WI, USA) with an 8-channel head coil. The phantom dataset was scanned by a gradient echo sequence (TE/TR =20 ms/35 ms, matrix size 384×384, flip angle 25, bandwidth (BW) = 80 Hz/pixel, FOV =240×240 mm2, number of slices 10, and slice thickness 5 mm). The axial brain dataset was acquired with a gradient echo sequence (TE/TR =20 ms/35 ms, matrix size 256×256, BW =100 Hz/pixel, flip angle 12, FOV =240×240 mm2, number of slices 20, and slice thickness 5 mm). All in vivo data were collected from healthy adult human volunteers with written informed consent. The study was approved by the Institutional Review Board.
Phase reconstruction
The reconstruction quality of CODEC was compared against those of MW (13) and MCPC-C (9). In our implementation of CODEC, a 7×7 (PE × FE) kernel was adopted for estimating coil sensitivity and combining coil images. To investigate the effect of accelerated sampling on the phase quality, the coil combination was performed on varying accelerated sampling factors. The under sampling k-space data were first reconstructed with parallel imaging method GRAPPA.
Phase unwrapping and removal of background field were performed after coil combination. In this study, phase region expanding labeler for unwrapping discrete estimates (PRELUDE) (41) was utilized to unwrap the phase. Before that, the phase image was multiplied with a mask image that was obtained with the erosion of the binary virtual reference image. Finally, a Gaussian low-pass filter was applied to remove the background field.
All image reconstructions were performed in Matlab (MathWorks, Natick, MA, USA) on a Windows 7 computer equipped with an Intel Celeron G540, 2.50 GHz CPU, and 4 GB RAM.
Quantitative evaluation
For the quantitative evaluation of reconstruction accuracy, the quality of phase matching between channels for the phantom data set was calculated as follows:
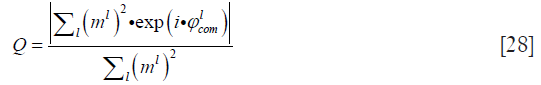
where ml and 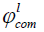 are the magnitude and combined phase of coil element l, respectively.
are the magnitude and combined phase of coil element l, respectively.
Gray matter to white matter CNR was compared for the brain data set. Mean CNR values were computed from 50 pairs of manually defined neighboring gray/white matter regions of interest (ROIs) from both cortical regions and deep structures. The ROIs were defined on the sum of the combined phase data from MW, MCPC-C, and CODEC to avoid potential bias. The contrast was computed as the difference between the mean values of the ROI pair and the noise as the mean of the two standard deviations that were computed (42).
Results
Figure 4 shows the phantom phase images reconstructed by MW (left), MCPC-C (middle), and the proposed CODEC method (right) under different data sampling scenarios: full sampling (upper), R=3 (middle) and R=4 (bottom). Serious phase wrapping and phase inconsistency artifacts can be viewed in the MW reconstructed phase images. Obvious phase wrapping and SNR degradation can be observed in the bottom right of MCPC-C reconstructed phase images. Minimal noise can be seen in the CODEC reconstructed phase image at the full sampling scenario, while the noise region increases at R=4.
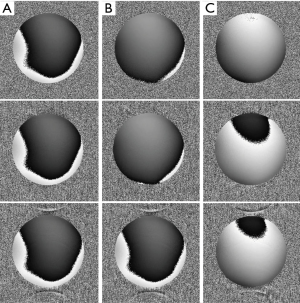
Figure 5 compares the magnitude images reconstructed by the SOS and CODEC. The visual difference is barely discernible between these two magnitude images. The difference image between these two magnitude images shows that magnitudes reconstructed by these two methods are nearly the same except for the region around the skull.
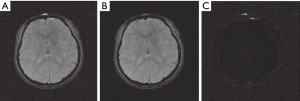
Figure 6 shows the brain phase images reconstructed by MW (left), MCPC-C (middle), and the proposed CODEC method (right). Both the MW and MCPC-C reconstructed phase images contain serious inconsistency and wrapping. By contrast, as expected, less noise can be observed in the CODEC reconstructed image.

Figure 7 shows the results after post-processing of brain phase images reconstructed by MW (left), MCPC-C (middle), and the proposed CODEC method (right). MW and MCPC-C show a localized hyper-intense inhomogeneity. By contrast, the CODEC reconstructed result has a more uniform distribution of intensity. Quantitatively, the mean CNR of the CODEC reconstruction is 3.42%, which is higher than that of the MW (2.95%) and MCPC-C (3.18%) reconstructions.
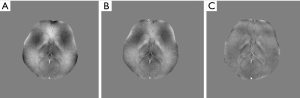
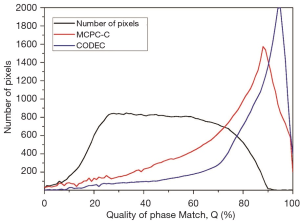
Figure 8 compares the histograms of quality factors over the whole brain in Figure 7. Q values are indistinguishable between MW, MCPC-C, and CODEC. The result of MW has more poorly matched pixels than that of MCPC-C and CODEC. CODEC produces more perfectly matched pixels than the other two.
Discussion
We here present a k-space-based method for combining phase images from phased array coils. The proposed method computes the coil combination weights through deconvolution in k-space to alleviate the influence of the noise and aliasing artifacts in the magnitude images at accelerated sceneries. The proposed approach was tested and validated with coils of diverse designs in the water phantom and brain. Compared with MW and MCPC-C, the proposed method based on the magnitude information and phase information of the images reconstructs the phase with much reduced noise and artifacts.
Currently, phase combination is still an intractable problem. Firstly, the phase varies weakly due to the weak susceptibility of biological tissue; thus, the phase needs to be carefully processed. However, earlier parallel MRI reconstruction methods aim to obtain high SNR for magnitude but not the phase. Secondly, owing to the imperfect shimming and varying coil sensitivity, the phase received by each coil is a summation of the coil sensitivity phase, the background field phase, and the proton phase. Furthermore, the phase from coil sensitivity and the background field is rarely measured in clinical application. As with magnitude, the coil combination is performed to remove the phase from coil sensitivity and the background field. Lastly, the phase reconstructed with arc tangent is wrapped into the range of (−π, π]; nonetheless, the absolute phase of proton distributes more widely. Therefore, phase unwrapping needs to be performed to obtain the absolute phase of the proton. Phase unwrapping is carried out for each coil before a coil image combination that is computationally intensive. By contrast, the proposed method performs phase unwrapping on the combined phase image because the coil image is combined in k-space. Hence, the proposed method is more efficient than the image-based combinations, although the proposed method has a prolonged procedure. Furthermore, impertinent coil combination would yield more noise and artifact in the combined phase image, which could increase the difficulty of phase unwrapping. The result in Figure 7 demonstrates that noise and artifacts are significantly reduced with the proposed method.
In addition, the method proposed in this paper achieves the combination of multi-coil data in k-space. After the inverse Fourier transform, both magnitude and phase information can be obtained simultaneously. As an added contribution, the proposed method can be used as a candidate for the combination of magnitude images.
The proposed method uses truncated coil sensitivity as the convolution kernel, which assumes that coil sensitivity information can be represented by the truncated region data. A convolutional kernel with a larger size has complete information but involves a more intensive computational load. Consequently, the optimal convolutional kernel size is a trade-off between computational complexity and performance. In this paper, a 7×7 convolution kernel was selected empirically in the experiments. The data distribution would be changed for different tissues in practical situations. Therefore, selecting the convolutional kernel by combining the histogram distribution of k-space data should be considered in future work. In further study, applying the proposed method on the reconstruction of QSM data would validate the clinical performance of the proposed algorithm.
Conclusions
This study demonstrated a novel coil combination method termed CODEC. The experimental results show that CODEC can alleviate the phase cancellation and phase wrapping in coil combination, and yield better image quality than some other start-of-the art methods.
Acknowledgments
The authors gratefully acknowledge the helpful comments and suggestions of the editor and reviewers, which will improve the presentation.
Funding: This work is partially supported by the National Science Foundation of China (Grant No. 81501548, 81501547, 61728107, and 61802352) and the Scientific Research Foundation of the Chengdu University of Information Technology (CUIT) (Grant No. KYTZ201805).
Footnote
Conflicts of Interest: The authors have no conflicts of interest to declare.
Ethical Statement: All in vivo data were collected from healthy adult human volunteers with written informed consent. The study was approved by the Institutional Review Board
References
- Hendee WR, Ritenour ER. Medical imaging physics. Hoboken, New Jersey: John Wiley & Sons, 2003.
- Ogawa S, Lee TM, Kay AR, Tank DW. Brain magnetic resonance imaging with contrast dependent on blood oxygenation. Proc Natl Acad Sci U S A 1990;87:9868-72. [Crossref] [PubMed]
- Austin C, McRee C, Ray J, Zetir M, Shapiro B. Right ventricular ejection fraction, pulmonary artery size and pulsatility index estimated by cardiac magnetic resonance imaging predicts functional status in pulmonary arterial hypertension. J Am Coll Cardiol 2018;65:A1142. [Crossref]
- Zheng Q, Feng Y, Wei X, Feng M, Chen W, Lu Z, Xu Y, Chen H, He T. Automated interventricular septum segmentation for black-blood myocardial T2* measurement in thalassemia. J Magn Reson Imaging 2015;41:1242-50. [Crossref] [PubMed]
- Yang G, Zhang Q, Tang G, Xu H, Yang Z, Guo J, Liang L, Qi Y. Role of magnetic resonance spectroscopy and susceptibility weighted imaging in cerebral alveolar echinococcosis. Iran J Parasitol 2015;10:122-7. [PubMed]
- Lindenberg KS, Weydt P, Müller HP, Bornstedt A, Ludolph AC, Landwehrmeyer GB, Rottbauer W, Kassubek J, Rasche V. Two-point magnitude MRI for rapid mapping of brown adipose tissue and its application to the R6/2 mouse model of Huntington disease. PLoS One 2014;9:e105556. [Crossref] [PubMed]
- Schäfer A, Turner R. A general method for generating multichannel phase images without using a body coil. ISMRM Workshop on High Field Systems and Applications; 2008.
- Zhong K, Leupold J, von Elverfeldt D, Speck O. The molecular basis for gray and white matter contrast in phase imaging. Neuroimage 2008;40:1561-6. [Crossref] [PubMed]
- Hammond KE, Lupo JM, Xu D, Metcalf M, Kelley DA, Pelletier D, Chang SM, Mukherjee P, Vigneron DB, Nelson SJ. Development of a robust method for generating 7.0 T multichannel phase images of the brain with application to normal volunteers and patients with neurological diseases. Neuroimage 2008;39:1682-92. [Crossref] [PubMed]
- Rauscher A, Sedlacik J, Barth M, Mentzel HJ, Reichenbach JR. Magnetic susceptibility-weighted MR phase imaging of the human brain. AJNR Am J Neuroradiol 2005;26:736-42. [PubMed]
- Stüber C, Pitt D, Wang Y. Iron in multiple sclerosis and its noninvasive imaging with quantitative susceptibility mapping. Int J Mol Sci 2016;17. [Crossref] [PubMed]
- Schenck JF. The role of magnetic susceptibility in magnetic resonance imaging: MRI magnetic compatibility of the first and second kinds. Medical Physics 1996;23:815-50. [Crossref] [PubMed]
- Roemer PB, Edelstein WA, Hayes CE, Souza SP, Mueller OM. The NMR phased array. Magn Reson Med 1990;16:192-225. [Crossref] [PubMed]
- Bernstein MA, Grgic M, Brosnan TJ, Pelc NJ. Reconstructions of phase contrast, phased array multicoil data. Magn Reson Med 1994;32:330-4. [Crossref] [PubMed]
- Xu L, Feng Y, Liu X, Kang L, Chen W. Robust GRAPPA reconstruction using sparse multi-kernel learning with least squares support vector regression. Magn Reson Imaging 2014;32:91-101. [Crossref] [PubMed]
- Larkman DJ, Nunes RG. Parallel magnetic resonance imaging. Phys Med Biol 2007;52:R15-55. [Crossref] [PubMed]
- Schweser F, Robinson SD, de Rochefort L, Li W, Bredies K. An illustrated comparison of processing methods for phase MRI and QSM: removal of background field contributions from sources outside the region of interest. NMR Biomed 2017;30:e3604. [Crossref] [PubMed]
- Robinson SD, Bredies K, Khabipova D, Dymerska B, Marques JP, Schweser F. An illustrated comparison of processing methods for MR phase imaging and QSM: combining array coil signals and phase unwrapping. NMR Biomed 2017;30:e3601. [Crossref] [PubMed]
- Haacke EM, Xu Y, Cheng YCN, Reichenbach JR. Susceptibility weighted imaging (SWI). Magn Reson Med 2004;52:612-8. [Crossref] [PubMed]
- Rauscher A, Barth M, Herrmann KH, Witoszynskyj S, Deistung A, Reichenbach JR. Improved elimination of phase effects from background field inhomogeneities for susceptibility weighted imaging at high magnetic field strengths. Magn Reson Imaging 2008;26:1145-51. [Crossref] [PubMed]
- Li W, Wu B, Liu C. Quantitative susceptibility mapping of human brain reflects spatial variation in tissue composition. Neuroimage 2011;55:1645-56. [Crossref] [PubMed]
- Lim IAL, Li X, Jones CK, Farrell JAD, Vikram DS, van Zijl PCM. Quantitative magnetic susceptibility mapping without phase unwrapping using WASSR. NeuroImage 2014;86:265-79. [Crossref] [PubMed]
- Fortier V, Levesque IR. Phase processing for quantitative susceptibility mapping of regions with large susceptibility and lack of signal. Magn Reson Med 2018;79:3103-13. [Crossref] [PubMed]
- Deistung A, Schweser F, Reichenbach JR. Overview of quantitative susceptibility mapping. NMR Biomed 2017;30:e3569. [Crossref] [PubMed]
- Thunberg P, Karlsson M, Wigström L. Comparison of different methods for combining phase-contrast images obtained with multiple coils. Magn Reson Imaging 2005;23:795-9. [Crossref] [PubMed]
- Lu K, Liu TT, Bydder M. Optimal phase difference reconstruction: comparison of two methods. Magn Reson Imaging 2008;26:142-5. [Crossref] [PubMed]
- Wang J, Kluge T, Nittka M, Jellus V, Kuehn B, Kiefer B. Parallel acquisition techniques with modified SENSE reconstruction mSENSE. Proceedings of the First Würzburg Workshop on Parallel Imaging Basics and Clinical Applications; 2001.
- Walsh DO, Gmitro AF, Marcellin MW. Adaptive reconstruction of phased array MR imagery. Magn Reson Med 2000;43:682-90. [Crossref] [PubMed]
- Chen Z, Johnston LA, Kwon DH, Oh SH, Cho ZH, Egan GF. An optimised framework for reconstructing and processing MR phase images. Neuroimage 2010;49:1289-300. [Crossref] [PubMed]
- Stevick JW, Harding SG, Paquet U, Ansorge RE, Carpenter TA, Williams GB. Gaussian process modeling for image distortion correction in echo planar imaging. Magn Reson Med 2008;59:598-606. [Crossref] [PubMed]
- Parker DL, Payne A, Todd N, Hadley JR. Phase reconstruction from multiple coil data using a virtual reference coil. Magn Reson Med 2014;72:563-9. [Crossref] [PubMed]
- Markl M, Frydrychowicz A, Kozerke S, Hope M, Wieben O. 4D flow MRI. J Magn Reson Imaging 2012;36:1015-36. [Crossref] [PubMed]
- Rodgers CT, Robson MD. Coil combination for receive array spectroscopy: Are data-driven methods superior to methods using computed field maps? Magn Reson Med 2016;75:473-87. [Crossref] [PubMed]
- Bollmann S, Robinson SD, O'Brien K, Vegh V, Janke A, Marstaller L, Reutens D, Barth M. The challenge of bias-free coil combination for quantitative susceptibility mapping at ultra-high field. Magn Reson Med 2018;79:97-107. [Crossref] [PubMed]
- Zhao F, Fessler JA, Wright SM, Noll DC. Regularized estimation of magnitude and phase of multi-coil b1 field via Bloch-Siegert B1 mapping and coil combination optimizations. IEEE Trans Med Imaging 2014;33:2020-30. [Crossref] [PubMed]
- Conturo TE, Smith GD. Signal-to-noise in phase angle reconstruction: dynamic range extension using phase reference offsets. Magn Reson Med 1990;15:420-37. [Crossref] [PubMed]
- Pelc NJ, Sommer FG, Li KC, Brosnan TJ, Herfkens RJ, Enzmann DR. Quantitative magnetic resonance flow imaging. Magn Reson Q 1994;10:125-47. [PubMed]
- Beatty PJ, Chang S, Holmes JH, Wang K, Brau AC, Reeder SB, Brittain JH. Design of k-space channel combination kernels and integration with parallel imaging. Magn Reson Med 2014;71:2139-54. [Crossref] [PubMed]
- Sodickson DK, Manning WJ. Simultaneous acquisition of spatial harmonics (SMASH): fast imaging with radiofrequency coil arrays. Magn Reson Med 1997;38:591-603. [Crossref] [PubMed]
- Griswold MA, Jakob PM, Heidemann RM, Nittka M, Jellus V, Wang J, Kiefer B, Haase A. Generalized autocalibrating partially parallel acquisitions (GRAPPA). Magn Reson Med 2002;47:1202-10. [Crossref] [PubMed]
- Jenkinson M. Fast, automated, N-Dimensional phase unwrapping algorithm. Magn Reson Med 2003;49:193-7. [Crossref] [PubMed]
- Eckstein K, Dymerska B, Bachrata B, Bogner W, Poljanc K, Trattnig S, Robinson SD. Computationally Efficient Combination of Multi-channel Phase Data From Multi-echo Acquisitions (ASPIRE). Magn Reson Med 2018;79:2996-3006. [Crossref] [PubMed]