
Rapid determination of internal strains in soft tissues using an experimentally calibrated finite element model derived from magnetic resonance imaging
Introduction
Magnetic resonance imaging (MRI) is commonly utilized in medical imaging to visualize hydrated structures such as tendon, cartilage, and intervertebral discs (IVDs) (1-3). MR imaging allows for differentiation between underlying tissue structures, and is informative for the diagnosis of injury and disease (4-6). A three-dimensional image stack from an MRI system provides the opportunity to examine tissue structures in a noninvasive manner, and build finite element models (FEMs). FEMs make it possible to simulate local tissue behavior to investigate loading conditions that are not feasible to examine experimentally (7-10). Applied to medical images, FEM also allows the evaluation of internal strains resulting from injurious and physiological loading scenarios. The accuracy of this type of simulation relies on experimentally calibrated boundary conditions that are dependent on the image acquisition protocol and MRI system.
To determine the feasibility of converting MR images of biological soft materials into a FEM, geometric meshes were generated by scanning a ballistic gel (commonly used to mimic human tissues) and a bovine IVD motion segment using a 0.6 Tesla (T) MRI system. The experimental design allowed the validation of the boundary conditions of these materials under loaded conditions and optimization of the mesh density used in the models. In this study, the ballistic gel simulations converged and generated a distribution of internal strains consistent with the strain distributions of a homogeneous soft material under compression. The bovine IVD simulations showed that the nucleus pulposus (NP) experiences greater strains than the annulus fibrosus (AF). When applied to a human lumbar IVD image stack using the approximate axial weight of an adult male torso, the AF and NP internal strain distributions similar to the loaded bovine IVD. Taken together, this approach can be broadly applied to soft biological materials to examine the internal strains experienced during physiological loading.
Methods
Determination of boundary conditions
Spherical ballistic gel
Ballistic gel (Gelatin#0, Hummic Medical, Greenville, SC, USA) was formed into a spherical gel with a diameter of 68 mm using a 3D printed mold. The spherical gel was inserted in a custom-built compression device made by two parallel acrylic plates, attached by four 6-cm long screws that allowed for height adjustment of the upper plate. A fluid based pressure sensor (iScan, Tekscan, Boston, MA, USA) was placed underneath the spherical gel to record the total force transmitted through the ball from the compression test. The spherical gel was compressed in steps of 5% total deformation until a 25% total deformation (17 mm) was achieved. The total compression force (N) was divided by the cross sectional area (mm2) at the mid-height (34 mm) of the ball to calculate an average stress (MPa).
Bovine functional spine unit (FSU)
A bovine FSU consisting of vertebrae-IVD-vertebrae was obtained from an ox tail approximately 6 months of age from a local abattoir. The FSU was tested intact to maintain the soft tissue constraints around the IVD. The IVD had a height of 10 mm measured from an MR image. The specimen was compressed until it reached 20% deformation of the IVD (2 mm) using a 5866 model Instron (Instron, Norwood, MA, USA) in displacement control mode. A maximum force reading was obtained from the Instron during compression. The total compressive force (N) was divided by the cross sectional area (mm2) at the mid-height (5 mm) of the IVD, determined using a digital xray taken from three orthogonal views, to calculate an average stress (MPa).
Image acquisition and mesh creation
A positional MRI system (Fonar, New York, NY, USA) (pMRI) was used to image the spherical gel, bovine IVD, and a human participant (imaged in standing). The human participant that gave informed consent based on previous criteria (3). Images were obtained from a 0.6T pMRI (Fonar, New York, NY, USA) using a 3-plane localizer to acquire sagittal T2 weighted images (repetition time =610 ms, echo time =17 ms, field of view =24 cm, acquisition matrix =210×210, slice thickness =3 mm, no gap, scan duration =2 min) (3,11), resulting in voxels of 3 mm × 1.5 mm × 1.5 mm from the pMRI scan. Segmentation of this volumetric pMRI data was performed using an image analysis software, Amira (Visage Imaging, Inc., San Diego, CA, USA). The segmentation technique combines auto-thresholding and manual segmentation utilizing image histograms to statistically separate voxels from the foreground and background of the image. The auto-threshold uses an upper and lower limit that is chosen based on the resolution and pixel intensity of the original image. A 3D tetrahedral model, which allows 6 degrees of freedom: 3 translational and 3 rotational, was generated and imported into Abaqus CAE (Dassault Systemes Americas Corp., Waltham, MA, USA) for FE analysis.
The L4/L5 motion segment was contoured from the lumbar spine MRI prior to segmentation. For both the bovine and human IVDs the value for auto-thresholding was obtained by averaging the two IVDs, and for the spherical ball only one auto-threshold value was used to separate the foreground (ball) from the background (air). These values determined the separation between the AF and NP where intensity values above the range were considered NP. After application of the auto-thresholding, manual segmentation was performed to clean up the image by smoothing out areas of intersection and pixel islands. The resulting image stacks were first segmented on the YZ-plane by thresholding and removing islands of pixels. Manual segmentation was then done on the XY- and XZ-planes to clean up the disconnected voxels. A surface model was then generated with a marching cubes algorithm (12). The AF and NP were given unique labels and faces to provide two meshes. The number of faces were adjusted, and the models were checked for any anomalies on the surface such as Intersections test, Closedness test, Orientation test, Aspect ratio (<20), Dihedral angle (>10) and Tetra quality (<20). Tetrahedral models were subsequently generated and exported to Abaqus.
Simulations
Spherical ballistic gel
The segmented mask of the spherical ballistic gel was exported into Abaqus. To replicate the experimental conditions in Abaqus, block parts were created to simulate the compression test. The block parts were placed over and under the sphere model. The sphere model used a 10-node quadratic tetrahedron element (C3D10) and the blocks generated in Abaqus used a 20-node quadratic brick, reduced integration element (C3D20R). The blocks were made of acrylic plastic and therefore had a material properties of E =3.10 GPa, and ν =0.3 (Matweb). The sphere ballistic gel material properties were determined experimentally to be E =0.03 MPa and ν =0.3. The interaction between the sphere and the blocks were given a friction penalty of 0.5 and the displacement of the upper block was 17 mm in the negative Z-direction to simulate approximately 25% deformation. The lower block was fixed (ENCASTRE U1 = U2 = U3 = UR1 = UR2 = UR3 =0). Furthermore, the Z-axis of the sphere was fixed in the X- and Y-direction to stabilize the sphere during compression.
Bovine FSU
The generated files for the AF and NP from the bovine functional spinal unit were imported into Abaqus for simulation. Material properties of a human IVD were used instead of bovine IVD. The material properties are E =4.2 MPa and ν =0.45 for the AF and E =0.2 MPa and ν =0.49 for the NP (13). The mesh for the AF was a 10-node quadratic tetrahedron elements (C3D10). The mesh for the NP was a 10-node quadratic tetrahedron with a hybrid element (C3D10H) due to its high Poisson’s ratio. The interaction between the AF and NP had a friction penalty of 0.2 and a tie constraint between the AF and NP was created. Boundary conditions were applied to the inferior and superior side of the AF where the inferior side was fixed (ENCASTRE U1 = U2 = U3 = UR1 = UR2 = UR3 =0) and the superior side was assigned a vertical displacement in the negative Z-direction of 2 mm.
Human IVD
The generated 3D tetrahedral model of the human AF and NP were imported as an input file into Abaqus CAE for FE analysis. Healthy human IVD material properties were used E =4.2 MPa and ν =0.45 for the AF; E =0.2 MPa and ν =0.49 for and NP (13). The mesh for AF was a 10-node quadratic tetrahedron element (C3D10). The mesh for NP was a 10-node quadratic tetrahedron with a hybrid element (C3D10H) due to its high Poisson’s ratio. The interaction between the AF and NP had a friction penalty of 0.2 and a tie constraint between the AF and NP was created. Boundary conditions were applied to the inferior and superior side of the AF where the inferior side was fixed (ENCASTRE U1 = U2 = U3 = UR1 = UR2 = UR3 =0) and the superior side was assigned a traction force of 0.3MPa, which correspond to the approximate static forces imposed on the lumbar spine in standing. This was applied uniformly across the superior surface at the angle of the L4/L5 IVD.
Mesh convergence study
To compare experiment and simulation, mesh sizes were down scaled using a successive marching cubes algorithm that resulted in fractions of the original number of faces from the initial surface model. Fractions from 5–75% of the original number of faces were selected to optimize computing time and the mesh density. The simulations were allowed to converge, and the resulting boundary stresses were then compared with those obtained from the experiments.
Results
Soft biological material finite element generation (Figure 1)

A sphere gel and bovine IVD were imaged using a pMRI (Figure 1A,D) and then converted to meshes of varying densities ranging from 0.1 to 0.75 of the initial number. Two representative meshes which have a mesh density of 0.3 of the initial number of faces show that the native geometry is preserved (Figure 1B,E). All simulations successfully converged and the typical runtime for simulations varied from 6 minutes to 2 hour and 30 minutes depending on mesh density. Stress distributions from the FEMs were obtained and displayed in a cut view for the sphere gel and bovine IVD models (Figure 1C,F).
Mesh convergence of models
A convergence test was performed on each model using the experimental results. The mesh size was normalized to the initial number of faces by dividing by the initial number of faces. The sphere gel needed five different mesh sizes to achieve an asymptotic curve that approached the experimental results (Figure 2A). The bovine IVD required seven different mesh sizes to obtain a convergence curve (Figure 2B). The optimal mesh size was found to be around a third of the original maximum mesh where the simulated value intersected the experimental results. The experimental stress value for the sphere gel is 1.42 MPa and for the bovine IVD is 3.03 MPa.

Internal strain distributions
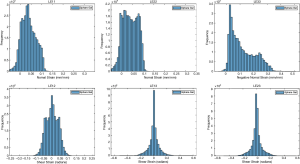
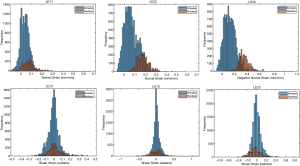
The ballistic gel showed a diverse range of principal and shear strains (Figure 3). The NP and AF compartments in the bovine IVD exhibited distinct distributions of principal and shear strains (Figure 4).
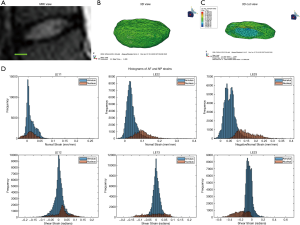
Human lumbar IVD
The optimal mesh density of 0.3 determined by our convergence study was used on an MRI stack of a human L4/L5 disc (Figure 5A,B,C). The simulation generated internal strain values (Figure 5D) for the AF and NP. Similarly to the bovine IVD, the NP has a different strain distribution from the AF.
Discussion
This study developed and validated an MRI-based FEM in multiple soft biological materials. Although FEM can be conducted with far more sophisticated assumptions, material models, and meshing strategies, the sophistication comes at the expense of computation time (14-23). Here we demonstrated that it is possible to conduct these simulations in around six minutes using a standard desktop computer, enabling the possibility of rapid examination of patient models in a clinical setting. We also employed the technique on one model of a human L4/L5 motion segment with a runtime under 10 minutes.
The ballistic sphere gel and bovine IVD were meshed from volumetric MR images and then calibrated against displacement controlled experiments as the boundary conditions. The derived optimal mesh size from the voxel based images is about a third of the initial number of faces. Using these calibrated models, we observed a range of internal strains in the NP and AF within the bovine IVD. This technique could be applied to any soft biological material examined using a three dimensional clinical imaging modality such as ultrasound. The thresholding and mesh generation from MR images is most efficient for contrasting hydrated tissues, such as the bovine IVD where two the components, NP and AF, contain distinct levels of hydration. Leveraging this principle, we believe this technique will be applicable to in vivo measurements due to the increased hydration in various tissues of interest.
The mesh generated from the DICOM image stacks can be reduced by as much as one third and still converge with the experimental results, suggesting that tissues of this geometry at this scale are not overly sensitive to the meshing density. In the bovine IVD, we achieved excellent correspondence with experimental results at a mesh density ratio 0.30 or higher. At this ratio, the computation time was reduced by 3.5 fold compared to the 0.8 mesh ratio. The simulations for mesh density ratios above 0.3 were all within 5% of the experimental measurement, while the sphere gel simulations with mesh ratios above 0.2 are within 6% of the experimental condition. These results suggest that the simulation has minimal improvement with increased mesh density, thus only increasing the run time of the model.
In the ballistic gel, which is a homogeneous material, the material properties can be experimentally determined. In the bovine IVD, we relied on published values of modulus and Poisson’s ratio for a healthy human AF and NP (13). This allowed us to examine the internal strain behavior within these two compartments, enabling effective modeling of the healthy IVD under non-damaging conditions. Accordingly, simulations showed that the bovine NP experiences greater internal strains than the AF similar to what has been observed in previous axial compression tests (18). It is worth noting that more sophisticated constitutive models can be implemented in order to capture damage and nonlinear processes, though the complexity would increase computation time. Though there are other efforts to model soft tissues from MR images using high field strength MRI (17-20,23), however, these were acquired in the supine position with minimal axial loading. Imaging combined with in situ loading is valuable for determining the load-response of articular cartilage and the IVD (14-16), but this approach has not yet been implemented in living humans. We have previously shown that the lumbar spine undergoes non-uniform segmental adaptations in standing (3), and the simulation conducted here is based on a standing image, which may be more relevant in loading-induced low back pain (24-26). Applying this approach to the MRI of the human lumbar segment in the upright position, we are able to model the internal strains based on the true geometry of the lumbar alignment in standing. Because the lumbar alignment changes between standing and supine, it is likely that we would be able to acquire more physiologically-relevant, load-dependent information from models created from the standing images.
In conclusion, we have generated meshes from volumetric MR images, and used them in an FEM calibrated from an experimental workflow. This technique can be applied to any musculoskeletal soft biological material that can be imaged with an MRI. We showed this techniques’ ability to be used in humans by applying it to an L4/L5 IVD where we successfully separated the strains of the NP and AF. The run time for the model was under 10 minutes making it possible to obtain an MRI and run the FEM within an hour at the clinic. This could help identify discs that are more susceptible to high loads which could lead to injury, as well as allowing clinicians to design localized strategies for low back pain prevention.
Acknowledgments
Funding: WUSTL Musculoskeletal Research Center (NIH P30 AR074992), NIH K01AR069116, NIH R21AR069804, NIH R01AR074441 and NIH 5T32EB018266.
Footnote
Conflicts of Interest: The authors have no conflicts of interest to declare.
References
- Berry DB, Hernandez A, Onodera K, Ingram N, Ward SR, Gombatto SP. Lumbar spine angles and intervertebral disc characteristics with end-range positions in three planes of motion in healthy people using upright MRI. J Biomech 2019;89:95-104. [Crossref] [PubMed]
- Gold GE, Han E, Stainsby J, Wright G, Brittain J, Beaulieu C. Musculoskeletal MRI at 3.0 T: Relaxation Times and Image Contrast. AJR Am J Roentgenol 2004;183:343-51. [Crossref] [PubMed]
- Weber CI, Hwang CT, Van Dillen LR, Tang SY. Effects of standing on lumbar spine alignment and intervertebral disc geometry in young, healthy individuals determined by positional magnetic resonance imaging. Clin Biomech (Bristol, Avon) 2019;65:128-34. [Crossref] [PubMed]
- Graichen H, von Eisenhart-Rothe R, Vogl T, Englmeier KH, Eckstein F. Quantitative assessment of cartilage status in osteoarthritis by quantitative magnetic resonance imaging: Technical validation for use in analysis of cartilage volume and further morphologic parameters. Arthritis Rheum 2004;50:811-6. [Crossref] [PubMed]
- Turecki MB, Taljanovic MS, Stubbs AY, Graham AR, Holden DA, Hunter TB, Rogers LF. Imaging of musculoskeletal soft tissue infections. Skeletal Radiol 2010;39:957-71. [Crossref] [PubMed]
- Weishaupt D, Zanetti M, Hodler J, Boos N. MR imaging of the lumbar spine: prevalence of intervertebral disk extrusion and sequestration, nerve root compression, end plate abnormalities, and osteoarthritis of the facet joints in asymptomatic volunteers. Radiology 1998;209:661-6. [Crossref] [PubMed]
- Dreischarf M, Shirazi-Adl A, Arjmand N, Rohlmann A, Schmidt H. Estimation of loads on human lumbar spine: A review of in vivo and computational model studies. J Biomech 2016;49:833-45. [Crossref] [PubMed]
- Dreischarf M, Zander T, Shirazi-Adl A, Puttlitz CM, Adam CJ, Chen CS, Goel VK, Kiapour A, Kim YH, Labus KM, Little JP, Park WM, Wang YH, Wilke HJ, Rohlmann A, Schmidt H. Comparison of eight published static finite element models of the intact lumbar spine: Predictive power of models improves when combined together. J Biomech 2014;47:1757-66. [Crossref] [PubMed]
- Peña E, Calvo B, Martínez MA, Palanca D, Doblaré M. Finite element analysis of the effect of meniscal tears and meniscectomies on human knee biomechanics. Clin Biomech (Bristol, Avon) 2005;20:498-507. [Crossref] [PubMed]
- Stadelmann MA, Maquer G, Voumard B, Grant A, Hackney DB, Vermathen P, Alkalay RN, Zysset PK. Integrating MRI-based geometry, composition and fiber architecture in a finite element model of the human intervertebral disc. J Mech Behav Biomed Mater 2018;85:37-42. [Crossref] [PubMed]
- Rodríguez-Soto AE, Jaworski R, Jensen A, Niederberger B, Hargens AR, Frank LR, Kelly KR, Ward SR. Effect of Load Carriage on Lumbar Spine Kinematics. Spine 2013;38:E783-91. [Crossref] [PubMed]
- Stalling D, Westerhoff M, Hege HC. Amira: A highly interactive system for visual data analysis. Vis Handb 2005;38:749-67.
- Polikeit A, Nolte LP, Ferguson SJ. The Effect of Cement Augmentation on the Load Transfer in an Osteoporotic Functional Spinal Unit: Finite-Element Analysis. Spine 2003;28:991-6. [Crossref] [PubMed]
- Butz KD, Chan DD, Nauman EA, Neu CP. Stress distributions and material properties determined in articular cartilage from MRI-based finite strains. J Biomech 2011;44:2667-72. [Crossref] [PubMed]
- Chan DD, Toribio D, Neu CP. Displacement smoothing for the precise MRI-based measurement of strain in soft biological tissues. Comput Methods Biomech Biomed Engin 2013;16:852-60. [Crossref] [PubMed]
- Chan DD, Neu CP. Intervertebral disc internal deformation measured by displacements under applied loading with MRI at 3T. Magn Reson Med 2014;71:1231-7. [Crossref] [PubMed]
- Jacobs NT, Cortes DH, Peloquin JM, Vresilovic EJ, Elliott DM. Validation and application of an intervertebral disc finite element model utilizing independently constructed tissue-level constitutive formulations that are nonlinear, anisotropic, and time-dependent. J Biomech 2014;47:2540-6. [Crossref] [PubMed]
- O’Connell GD, Vresilovic EJ, Elliott DM. Human intervertebral disc internal strain in compression: The effect of disc region, loading position, and degeneration. J Orthop Res 2011;29:547-55. [Crossref] [PubMed]
- OʼConnell GD. Johannessen W, Vresilovic EJ, Elliott DM. Human Internal Disc Strains in Axial Compression Measured Noninvasively Using Magnetic Resonance Imaging: Spine 2007;32:2860-8. [PubMed]
- Showalter BL, DeLucca JF, Peloquin JM, Cortes DH, Yoder JH, Jacobs NT, Wright AC, Gee JC, Vresilovic EJ, Elliott DM. Novel human intervertebral disc strain template to quantify regional three-dimensional strains in a population and compare to internal strains predicted by a finite element model. J Orthop Res 2016;34:1264-73. [Crossref] [PubMed]
- Tang SY, Souza RB, Ries M, Hansma PK, Alliston T, Li X. Local tissue properties of human osteoarthritic cartilage correlate with magnetic resonance T1rho relaxation times. J Orthop Res 2011;29:1312-9. [Crossref] [PubMed]
- Wan C, Ge L, Souza RB, Tang SY, Alliston T, Hao Z, Li X. T1ρ-based fibril-reinforced poroviscoelastic constitutive relation of human articular cartilage using inverse finite element technology. Quant Imaging Med Surg 2019;9:359-70. [Crossref] [PubMed]
- Yoder JH, Peloquin JM, Song G, Tustison NJ, Moon SM, Wright AC, Vresilovic EJ, Gee JC, Elliott DM. Internal Three-Dimensional Strains in Human Intervertebral Discs Under Axial Compression Quantified Noninvasively by Magnetic Resonance Imaging and Image Registration. J Biomech Eng 2014. [Crossref] [PubMed]
- Hwang CT, Van Dillen LR, Haroutounian S. Do Changes in Sensory Processing Precede Low Back Pain Development in Healthy Individuals? Clin J Pain 2018;34:525. [Crossref] [PubMed]
- Nelson-Wong E, Callaghan JP. Transient Low Back Pain Development During Standing Predicts Future Clinical Low Back Pain in Previously Asymptomatic Individuals. Spine 2014;39:E379. [Crossref] [PubMed]
- Sorensen CJ, Johnson MB, Callaghan JP, George SZ, Van Dillen LR. Validity of a paradigm for low back pain symptom development during prolonged standing. Clin J Pain 2015;31:652-9. [Crossref] [PubMed]


