A survey of GPU-based acceleration techniques in MRI reconstructions
Introduction
Parallel computing is a type of classic computation to speed up the computer speed (1). It can divide the large problems into lots of smaller ones. Their calculations are carried out simultaneously, or their process executions are carried out simultaneously. Parallel computing can bring higher-performance computation in comparison to the classic computation (2), but it generally requires hardware support. Parallel computing has become a dominant popular field in computer architecture paradigm (3), mainly in the form of multi-core processors parallel computing, for example, clusters computing, massively parallel computing (MPPs), grids computing, graphics processing units (GPU), etc. Recently, the progress of single-core processor performance has almost arrived at the physics limitations, and Moore’s law has become less effective to raise the computational feasibility of more complex algorithms. Instead, the scientists and engineers have to shift their algorithms of growing complexity to parallel computing architectures for decreasing practical processing times of their algorithms.
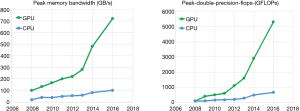
During the past few years, GPUs have been developed with incredible increase in number due to relatively cheap and high-performance calculation platforms for data parallel computing, especially in medical image reconstruction of massive data-set. General-purpose computing on GPUs (GPGPU) has been a fairly recent trend in parallel computing research. Among the GPGPU framework, the use of massive multiple graphics units in one computer can further parallelize the existing parallel nature of GPUs due to the specialization in each chip. It can provide some advantages of the higher-performance computation ability, which multiple CPUs cannot offer (4). However, the high-performance computation utilization on GPU or GPGPU requires reformulating current sequential computation problems in terms of graphics primitives, which have been supported on GPUs by the two major API libraries for graphics processors: OpenGL and DirectX. This cumbersome translation from general programming to GPU hardware was obviated by the obscure GPU programming languages such as Sh/RapidMind, Brook and Accelerator (5,6). But they are hard to be applied for the common programmers without corresponding programming training. To further provide real convenience to GPU programmers, three libraries, which are NVIDIA’s Compute Unified Device Architecture (CUDA), Microsoft’s DirectCompute and Apple/Khronos Group’s OpenCL, provided more feasible GPU programming frameworks for programmers to ignore the requiring full and explicit conversion of the data to the graphical forms and take advantages of the high-performance computing speeds on GPUs (7). Actually, a group at SGI Corporation has firstly implemented a GPU computing of image recon processing on an Onyx primitive workstation using the RealityEngine2.5 in 1994 (8). Because of the graphics-hardware limitations at that time, the SGI graphics-hardware implementation is 100 times slower than a single-core CPU processor in 2004 (8). However, the performance developments of recent single-core CPU processors have been much slower than the multi-core of GPU processors. Today, GPUs have been a standard hardware part of the current computers for graphics processing and are further designed as relatively independent frameworks for processing data parallel problems, which can assign individual element data to separate logical cores for complex processing [as seen in (9)]. As seen in Figure 1, it presents the evolution of bandwidth and computation abilities between GPUs and CPUs in GB/s and GFLOP/s (i.e., billions of data movement speed per second; billions of floating point operations per second under single and double precision situations) (10). If GPU is compared on a chip-to-chip basis against CPUs, GPUs can have much better capability on both key indexes, speed of calculation (FLOPS) and speed of data movement (GB/s) (10,11). Therefore, this development shift between GPUs and CPUs gives a new motivation for researchers to re-consider parallelizing their computations of medical image applications on GPU frameworks. Through directly inputting the data-parallel computation part onto GPUs, the number of physical computers within a computer can be greatly reduced to minimum. The benefits are not only reducing computer cost, but also requiring less maintenance, space, power, and cooling for whole system operation cost inside any institutes, schools or hospitals.
GPU computing
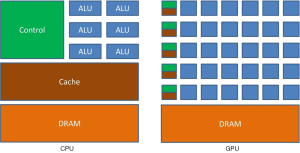
The physical architectures and processing model of GPU and CPU are very different, which is the main reason the computing power of GPU is much faster than CPU. As seen in Figure 2 (12), GPU has the features that can provide many data-parallel, high memory bandwidths and deeply multi-threaded cores for large number of simple computation tasks, but CPU just can provide the limited cores for high-complex computation tasks. Architecturally, as seen in Figure 2, the structure comparison between CPUs and GPUs in GLOP/s computation capability is that GPUs are highly specialized for compute-intensive, highly parallel computation hardware structure and design that over 80% of transistors are contributed for data processing rather than the data caching and flow control functions; on the contrary, CPUs are designed as a few cores with many cache memories for easily handling complex software threads at one time. For instance, a general GPU can have 100+ processing cores which can handle thousands of software threads simultaneously. In theory, the GPUs’ performance can be accelerated to process thousands of software threads by 100× over CPUs’ alone processing. Because of the special GPU architectures which are different from general CPU architectures, GPU codes can easily run algorithms in parallel. But in most cases of general CPU-based algorithm, there is no algorithm which can be suitable for GPUs, because the general algorithms are suitable for the general CPU architectures. The problems require that the general algorithms should be redesigned into new, more power- and cost-efficient parallel algorithms for GPUs’ special features. The parallel codes can certainly bring higher-performance for developed algorithms, and simultaneously bring more difficult debugging problems than general codes.
As we know, GPUs are primitively developed to accelerate the image processing speed of graphics cards. When graphics mode is turned on, based on the GPUs’ API such as OpenGL or DirectX, programmers can implement shading programs to custom the graphics pipelines of GPUs at run time, using high-level shading languages such as NVIDIAC for Graphics (CG), OpenGL Shading Language (GLSL), or Microsoft High-Level Shading Language (HLSL), Adobe Graphics Assembly Language (AGAL), Sony PlayStation Shader Language (PSSL), etc., which are originally designed for real-time rendering (2). Although early GPU computing programs have achieved impressive accelerations on medical image processing (13-16), they suffered from some drawbacks as follows. Firstly, the GPU computing coding is very difficult for entry-level programmer to develop the qualified code, because they need to be defined in terms of graphics concepts, for instance, vertices, texture coordinates, and fragments; secondly, acceleration performances of GPU computing codes are compromised by the lack of access to all the capabilities of GPUs, such as shared memory and scattered writes; thirdly, the code portability is constrained by the specific hardware features of some graphics extensions (8).
In order to solve the drawbacks, there are four major commercial framework solutions, CUDA, OpenCL, Stream and DirectCompute, which have been deployed to generate parallel higher-performance codes for GPU. Among them, CUDA was developed recently by NVIDIA; OpenCL is an open standard library that was developed by Khronos Group; Stream was developed by AMD (ATI chips); DirectCompute was developed by Microsoft (2). Among the solutions, CUDA is the solution that is most widely used to rewrite algorithms to be GPU-enabled and efficient by programmers in computer graphics, image processing, computer vision, computational fluid dynamics (CFD) and many more fields. The primary advantage of the CUDA framework is that it can easily bring the C/C++-like development environment and the parallel capabilities of GPU acceleration for programmers, but does not require programmers to have lots of detailed knowledge of GPU hardware architectures. Although they are much helpful for programmers to employ GPUs into the application, there are still some more consumable software packages based on CUDA and OpenCL libraries for the programmers who are not familiar with GPU programming and have finite C/C++ parallel programming experiences. Here, several popular libraries should be mentioned, Thrust, cuFFT, cuSOLVER, cuSPARSE, and cuDNN, which are widely used in applications ranging in the fields of signal processing and image processing (17,18). For example, Thrust is a derivative C++ template library for parallel GPU platforms based on the well-known CPU-based Standard Template Library (STL). It can provide programmer a shortcut to easily utilize prototype demos for high performance CUDA applications with minimal programming efforts through its high-level interfaces fully interoperable with technologies such as C/C++, CUDA, etc. (18). The cuFFT library provides a simple software interface based on the well-known Cooley-Tukey and Bluestein algorithms to get accurate Fourier transformation (FT) results faster than ever, and its speed of computing fast Fourier transforms (FFTs) is up to about 10× faster of computing discrete Fourier transforms for any complex or real-valued data sets. The cuSOLVER library provides a collection of dense and sparse direct solvers which can deliver significant accelerations for computer vision, CFD, and linear optimization applications. The cuSPARSE library including a sparse triangular solver provides a collection of basic linear algebra subroutines used for sparse matrices can deliver up to about 8× faster performance than the well-known Intel Math Kernel Library (MKL). As a GPU-accelerated version of the complete standard library, it can deliver 6× to 17× faster performance than the Intel MKL. The cuDNN library is a GPU-accelerated library for deep neural networks (NNs), which can provide highly tuned implementations for standard routines such as forward and backward convolution, pooling, normalization, and activation layers (18). The cuDNN library allows researchers to focus on training designed NNs and developing software applications rather than spending much time on realizing low-level GPU performance tuning. Now, cuDNN has been widely applied into many deep learning frameworks, such as, Caffe, TensorFlow, Theano, Torch, and so on. Actually, these libraries have enough ability to provide enough supports for most computations of algorithm operations in magnetic resonance image reconstruction. Therefore, providing the competitive ability of high-performance parallel computing supported by these libraries, GPU-based computing algorithms have been applied into the comprehensive applications of magnetic resonance image reconstruction, due to GPUs’ super-powerful parallel computing ability with multi-thread capabilities and multi-core architectural structures (19).
Magnetic resonance imaging (MRI) reconstruction
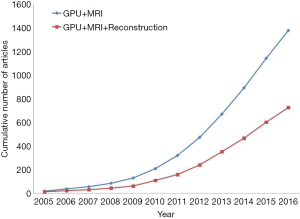
In clinical applications, MRI reconstruction calculations have become more and more complex for computers, so there are urgent speed requirements from doctors and scientists to review the patients’ images without too long waiting for reconstruction processing. Currently, GPU computing has been increasingly investigated for clinical MRI reconstruction applications (Table 1). According to statistics, there are lots of papers about GPU, MRI and reconstruction which are published from 2005 to 2016, as seen in Figure 3. This plot illustrates prevalence of GPU-based methods in the field of MRI reconstruction. It is explicit that GPU-accelerated MRI reconstructions became much more applicable especially after the release of NVIDIA’s CUDA in 2007 (47). Actually, the number of publications related to GPU and MRI always increases very quickly, but recently, the publications about GPU, MRI and reconstruction do not grow up synchronously. The growth is slowing down, because most of the GPU-accelerated algorithms about typical MRI reconstruction have been studied well and implemented on GPUs. Among these GPU-accelerated methods, they can roughly be divided into three categories of MRI reconstruction with GPU computing, FT, parallel imaging (PI), compressed sensing (CS), and deep learning, which are going to be introduced as follows. A summarization of GPU-based MRI reconstruction method is presented in the Table 1. Here, it is default to apply GPUs to accelerate deep learning applications, because GPUs are suitable for deep learning calculations. Otherwise, the CUDA library and hardware of NVIDIA Corp. have occupied the field of the GPU computation. It seems that the NVIDIA Tesla cards are not faster than the NVIDIA GeForce cards, but it is an illusion and NVIDIA Tesla cards are more powerful than NVIDIA GeForce cards. Actually, the speed-up factors of GPU-based MRI reconstruction depend on the system platforms, GPU-implementation and reconstruction algorithms.
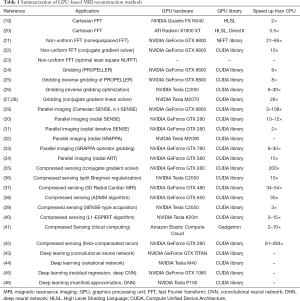
Full table
FT
Most MR imaging methods are designed based on Fourier encoding, so that methods in the MRI reconstructions include basic FFT. The FFT implementation on CPUs has already been quite efficient, but its version on GPUs can be accelerated faster than on CPUs. Actually, Sumanaweera et al. presented to implement the Cartesian FFT method as a multi-pass decimation-in-time butterfly algorithm on GPUs in the book of Ref. (19). They presented several specific approaches for obtaining higher performance, using two pbuffers and balancing some computing loads from fragment processors into the vertex processors and rasterizers. And they briefly illustrated the high-performance experiments of MRI reconstruction and ultrasonic imaging. Then, Schiwietz et al. described an efficient GPU-based implementation of the non-Cartesian FFT (20), which was written in primitive and underlying Microsoft’s DirectX with C/C++ and HLSL. They implemented a look-up-table (LUT)-based Kaiser-Bessel window gridding algorithm and a Ram-Lak filtered back-projection method. Their primary results showed the recon time and image quality for two GPU-based reconstruction algorithms that were comparable with the CPU-based implementations for radial trajectories. Otherwise, Sørensen et al. also presented a fast parallel GPU-accelerated algorithm to compute the nonequispaced FFT (21), in which the key step is implementing the convolution step in transform that was the most time consuming part before. The authors claimed that their GPU-accelerated convolution was up to 85 times faster than the open source NUFFT library (48), when using two MRI data-sets sampled by radial and spiral trajectories to estimate the algorithm performances. Actually, before the NVIDIA CUDA library appeared in June 2007, any implementation of relative complex algorithms was hard to be coded for programmers; even those have some GPU-based programming experiences.
Currently, NVIDIA has released their easy-to-use CUDA framework in which they realized the cuFFT library (49), which is an optimized GPU-based implementation of the FFT. There are two separate libraries: cuFFT and cuFFTW. The cuFFT library is designed to provide easy-to-use high-performance FFT computations only on NVIDIA GPU cards. While, the cuFFTW library is a porting tool that is provided to apply FFTW into users’ projects with a minimum amount of effort. Both two libraries can provide the features as follows (18): an O(nlogn) algorithm for different input data sizes; single-precision (i.e., 32-bit floating point) and double-precision (i.e., 64-bit floating point) computations; complex and real-valued digital input and output; execution of multiple 1D, 2D and 3D transforms simultaneously; most in-place and out-of-place FFT; arbitrary intra- and inter-dimension element strides. Here, Figure 4 shows a current example of using CUDA’s cuFFT library to calculate two-dimensional FFT, as similar as Ref. (49). They simply are delivered into general codes, which can bring the GPU-accelerated computation power for arbitrary projects.

Actually, Stone et al. have presented an anatomically constrained MR reconstruction algorithm based on NVIDIA’s CUDA library for non-Cartesian MR data (22). What is more, their algorithm could find the solution for a quasi-Bayesian estimation problem that is a typical problem in MRI reconstructions. Their results showed that their algorithm could reduce the recon time for an advanced non-uniform reconstruction of the in vivo data from 23 minutes on a quad-core CPU to about 1 minute on the Quadro Plex cluster, which can be applied to accelerate MR reconstruction into many clinical applications. Besides, Yang et al. presented optimized interpolators to approximate the non-uniform FT of a finitely supported function in the inversion of non-Cartesian data (23). According to their simulation applications, their interpolators could provide iterative non-Cartesian inversion algorithms which could reduce memory demands on memory limited early GPU systems. Moreover, Guo et al. improved a grid-driven interpolation algorithm for PROPELLER trajectory in real-time non-Cartesian applications (24). Their GPU-based method could be about 9 times faster than their implementation on CPU, and it could achieve compatible motion correction accuracy and image quality. Moreover, Yang et al. also presented a CUDA-based algorithm to raise the reconstruction efficiency of conventional PROPELLER trajectory (25). They developed a reverse gridding algorithm to reduce computation complexity. But different from the conventional gridding algorithm which generated a grid window for every trajectory, their algorithm calculated a trajectory window for every grid. The contribution of each k-space point in the convolution window was accumulated for this grid. Their experiments illustrated that its recon speed was 7.5 times faster than that of conventional gridding algorithm. Besides, Obeid et al. proposed a modified GPU-based gridding method to perform gridding using a graphics processor (GPU) to achieve up to 29× acceleration for three-dimensional gridding (26). Their solution was to allow bins to contain a variable number of sample points within them, without sacrificing rapid access. Furthermore, an image reconstruction GPU-accelerated software toolkit for reconstructing data from arbitrary 3D trajectories has been released in Ref. (27,28). It is named as the Illinois Massively Parallel Acquisition Toolkit for Image reconstruction with ENhanced Throughput in MRI (IMPATIENT MRI). In their toolkit, they removed computational bottlenecks using a gridding method to accelerate the computation of data structures by the previous routine. Furthermore, they enhanced the capabilities of off-resonance correction and multi-sensor PI reconstruction, with speeding up 200 times more than before (27). And they gained much efficient trajectories for high spatial and temporal resolution in the applications (28).
PI
PI (PMRI) techniques are employed to reconstruct under-sampled data in k-space by attaining complementary information from multiple receive coils. There are a lot of PMRI reconstruction techniques that have been proposed (50). Currently, among them, the most well-known PMRI techniques are mainly SMASH (51), SENSE (52), and GRAPPA (53). Most of these techniques require additional coil sensitivity maps to remove the artifact’s effect, because of acquisition data under-sampled in the k-space. If current PMRI methods are simply analyzed, they can be roughly- classified into two types (50): one is the reconstruction procedure in image space which includes unfolding operation and inverse procedure, for example, SENSE (52); another is the reconstruction procedure in k-space, which has kernel calculation and recovery procedures of missing k-space data, for instance, SMASH (51) and GRAPPA (53).
SENSE and SENSE derivative methods have been implemented in GPUs (29-33). For example, the GPU-based implementations of Cartesian SENSE and k-t SENSE have been presented by Hansen et al. in Ref. (29). They focused on the inversion problems of SENSE recon and solved them for each set of aliased pixels in image-space or x-f space, since these problems generally were the most time-consuming steps in the SENSE and SENSE derivative reconstructions. Here, Sørensen et al. presented a GPU-based reconstruction algorithm to enable real time reconstruction of sensitivity encoded none-Cartesian radial imaging (e.g., radial SENSE) (30). They claimed their algorithms could be used for real-time recon applications, because of using a moving buffer scheme to buffer the interval between data acquisition and image display. In addition, Sørensen et al. also have further described their real-time iterative SENSE GPU-based reconstruction to reduce the reconstruction time in the isotropic whole-heart imaging application, an important protocol in simplifying cardiac MRI (31). They have shown that the 3D datasets (256 slices) could be reconstructed in 5–6 minutes. As an important PMRI method, GRAPPA also has been implemented on GPUs. For example, Saybasili et al. presented an automatically distributed hybrid (multi-node, multi-GPU), low-latency through-time radial GRAPPA reconstruction pipeline in Ref. (32). Actually, they proposed a combined CPU- and GPU-based computation framework to use multi-threaded CPU and GPU programming on multiple nodes (32). In their implementation, the master node forwards raw data was to each node for partial processing, because GRAPPA generally requires using all coil data to separately recon coil by coil. Each node could distribute the task to its local GPUs, and send its partial image results back to the master node after reconstructions. After that, all image results were combined and sent to the scanner for display. Their implementation claimed their reconstruction performances on 32 coils could achieve 42 ms acquisition time, 11.2 ms reconstruction time for under-sampled radial datasets, and their methods could be utilized into more challenging reconstruction scenarios which have larger numbers of acquisition coils, higher acceleration rates, or more GPUs than before. Furthermore, Inam et al. proposed an acceleration method for Self-calibrating GRAPPA operator gridding by using massively parallel architecture of GPUs (33). The LUTs were used to pre-calculate all possible combinations of gridding weight as well as avoid the race condition among the CUDA kernel threads. Firstly, they used the LUT-based optimized kernels of CUDA to pre-calculate all the possible combinations of 2D-gridding weight sets, after that they applied appropriate weight sets to shift the radial acquisitions to the nearest Cartesian grid locations. They claimed that their GPU-based method could typically achieve 6× to 30× speed-up without compromising the image quality.
Actually, the above methods mainly attempted to transfer the classical PMRI methods based on CPUs into the GPU-based PMRI recon methods. However, the PMRI algorithms based on parallel GPUs should be re-designed according to the GPUs’ features. For example, Li et al. implemented a GPU-accelerated algebraic reconstruction technique (ART) reconstruction in Ref. (34) to apply to recover images with radial cardiac cine acquisitions. They mainly compared the reconstructed Cine images of their radial ART method with filtered back-projection at multiple under-sampling levels. Their results illustrated that GPU-accelerated ART could get comparable results in comparison with conjugate gradient SENSE in parallel radial MR imaging, and could also reduce artifacts and maintain image sharpness comparing with general filtered back-projection methods. Actually, the classical PMRI methods are not time-cost iterative methods; there are not huge improvements for GPU-based classical PMRI recon methods if the scenario is not extreme. However, for some nonlinear problems or complex iterative reconstructions in PMRI applications, GPU-based recon methods can bring lots of improvements if recon methods are designed according to the GPUs’ structure features.
CS
Recently, to solve a minimization problem in MRI reconstruction, CS was studied and started to be applied into MR applications (54). Because the NVIDIA CUDA library is more and more perfect to support for GPU computing, the complex sparse reconstruction methods are more easily implemented on GPUs without considering the hardware constrains on GPUs. Actually, there are recently some papers studying CS MR recon methods on GPU architectures (35-42). For example, Zhuo et al. presented a GPU-accelerated regularization reconstruction method with compensations for susceptibility-induced field inhomogeneity effects, which are incorporating a quadratic regularization term (35). In their experiments, they realized a GPU-based spatial regularization with sparse matrices, which of the entire procedure is enabled to be performed on GPUs and avoid the memory bandwidth bottlenecks which are associated with frequent communications between GPUs and CPUs. Recently, because of popular CS, many studies have applied GPU-accelerated computing for fast CS MRI reconstruction, which seemed to be ideally suited for CS recon (54). For instance, Smith et al. also have presented a GPU-accelerated Bregman solver to accelerate 2D CS reconstruction in Ref. (36). They demonstrated that their combination of the split Bregman method and GPU computing could achieve the rapid convergence and massive parallel computation of real-time CS reconstruction for small-to-moderate size images. Their GPU-accelerated iterative reconstruction method could reconstruct two-dimensional 1,0242 data matrices with a factor of up to 27 and spend about 0.3 seconds or less; even there is no available GPU VRAM. Nam et al. also proposed a parallelized GPU-accelerated implementation of an iterative CS reconstruction algorithm for 3D radial data acquisitions in both phantom and in vivo whole-heart coronary data sets (37). To reduce the time-cost operations of gridding and regridding operations, operations could be performed in a parallel manner for every measured radial point, suited for CUDA implementation. Comparing with the efficacy of the general CPU-implementation, their GPU-implemented CS reconstruction could improve image recon quality in terms of vessel sharpness and suppress noise-like artifacts, and reduce the running time of CS reconstruction to 34.3–53.9 times less than CPU-based C/C++ implementation. In addition, Chang et al. presented an efficient GPU-based method for CS-MRI reconstruction for 3D multichannel data (38). They built a highly-parallelized framework to compute the CS-MRI reconstructions of simultaneous multiple-channel 3D-CS reconstructions. The results of simulated data and in vivo data showed that the proposed efficient method can significantly shorten the reconstruction run-time by a factor of 30. Even in some clinical applications, the 3D multi-slice CS reconstruction of the proposed method allowed to be performed in less than 1 second.
Otherwise, there are also some other papers studying CS MR recon methods on several parallel architectures of multi-core CPUs and multi-core GPUs (39-41). They presented the huge potential speed-up ability on the architectures. For instance, Kim et al. investigated an inexact quasi-Newton CS reconstruction algorithm on several parallel processing architectures that included CPUs, GPUs, Intel’s Many Integrated Core (MIC) architecture, etc. (39). They have claimed lots of experiments on different parallel architectures (multi-core CPUs, GPUs, MIC, etc.). Among their experiments (39), their reference implementations on the 4-core Core i7 were able to reconstruct a 256×160×80 8-channel data of the neuro vasculature with a speedup of 10× under-sampled data set in 56 seconds; the recon time could be reduced further to 32 seconds on the 6-core Core i7; the CUDA-based implementation could reduce the reconstruction time to 16 seconds on NVIDIA GTX480; the recon time even could reduce to 12 seconds on the Intel’s Knights Ferry (KNF) of the MIC architecture. All their experiments showed that their CS algorithm could bring huge benefits from those throughput-oriented architectures. Apart from that, Sabbagh et al. studied to accelerate the non-linear CS reconstruction problem in cardiac MRI solved by iterative optimization algorithms and to facilitate the migration of CS reconstruction in the clinical applications (40). Their experiments employed 3D steady-state free precession MRI images from five patients, and compared the speed and recon image quality on different parallel platforms, such as CPU, CPU with OpenMP, and GPU. Their recon results showed that the mean reconstruction time was 13.1±3.8 minutes on the CPU platform, 11.6±3.6 minutes on the CPU platform with OpenMP, and 2.5±0.3 minutes for the CPU platform with OpenMP plus GPU (40). And their image qualities estimated by image subtraction were very similar, which are comparable on different parallel architectures. Otherwise, the modern cloud-computing conception also has been applied into time-cost MR reconstructions. Cloud-computing generally needs to support most of modern parallel architectures, GPUs are one of them. For example, Xue et al. utilized the open source Gadgetron framework to support distributed computing for image reconstruction and demonstrated that a multi-node version of the Gadgetron which could provide nonlinear image reconstruction with clinically acceptable latency (41). Actually, their framework was a cloud-enabled version of the Gadgetron on three different distributed computing platforms ranging from a heterogeneous collection of commodity computers to the commercial Amazon Elastic Compute Cloud (41). They claimed that they could provide nonlinear, CS reconstructions of cardiac and neuron imaging applications with low reconstruction latency. Besides, Zhuo et al. proposed an GPU-implemented reconstruction algorithm with MR field inhomogeneity compensation into calculating magnetic field maps and its gradients for iterative CG reconstruction algorithms on NVIDA CUDA-enabled GPUs (42). If comparing with their CPU-based implementations, their GPU-based implementations could hugely reduce the calculation time, while it could still guarantee acceptable accuracy to compensate MR field inhomogeneity.
Deep learning (DL)
Recent developments of DL in NNs have brought lots of breakthrough improvements in many areas (55-58). Because of the time-cost training and multiple-layer NNs, GPUs are very suitable for solving the massive calculation problems of DL (55). Although there are several attempts at creating fast NN-specific hardware, GPUs brought a real cheap way to implement DL in lots of applications. GPUs can be employed at not only the fast matrix and vector multiplications, but also for NN training, and speeding up DL by a factor of 50 and more (55). Currently, GPU-based DL started to be applied into some MR applications (43-46) as follows to solve the problems of MRI reconstruction.
Wang et al. firstly proposed a DL method to accelerate MR reconstruction (43). They built a big dataset of existing high-quality images, and trained an off-line 3-layer convolutional neural network (CNN) as the complex mapping between MR images from zero-filled and fully-sampled k-space data. Actually, the trained network can predict the under-sampled data, when solving an online constrained reconstruction problem. Although the off-line training can take roughly 3 days, it took less than 1 second for every online reconstruction-based GPU. The in vivo results illustrated that the proposed method can restore fine details and have great potential for effective MR imaging.
Hammernik et al. presented an efficient approach to learn a variational network which can remove typical under-sampling artifacts and restore important image details, such as the natural appearance of anatomical structures (44). They considered that their trained models were highly efficient and are also well-suited for parallel computation on GPUs, due to their structural simplicity. And their approach illustrated that they achieved superior results than many commonly used reconstruction methods.
Lee et al. expressed a novel deep residual learning algorithm to recover images from highly under-sampled k-space data (45). Here, they formulated a traditional CS problem as a residual regression problem, and designed a deep CNN to learn the aliasing artifacts. They trained the NN using the magnitude of MR images by a stochastic gradient descent method with momentum based on the MatConvNet toolbox (59) and NVIDIA GTX 1080 GPUs. They expressed that their algorithm took only about 30 ms after their deep CNN has been well trained, with much better reconstruction performance compared to many existing GRAPPA and CS algorithms.
Zhu et al. proposed an automated robust NN as a generalized reconstruction framework which can exploit the universal function approximation of multi-layer perception regression and the manifold learning properties demonstrated by auto-encoders (46). They implemented a unified reconstruction framework with a deep neural network (DNN) feed-forward architecture composed of fully-connected layers followed by a sparse convolutional auto-encoder. And they built their NN parameters which were trained to minimize squared loss and updated by a stochastic gradient descent, computed with the Tensorflow toolbox (60) and 2 NVIDIA Tesla P100 GPUs. And their results show to be over a lot of acquisition strategies, and have excellent immunity to noise and artifacts.
With fast developments of GPUs and DL in NNs, an exciting epoch of MRI reconstruction has started. Although it is still early to say the DL reconstruction approaches will replace currently used clinical methods, the development of the DL approaches has illustrated huge potential to promote the technology developments of MRI reconstruction and change these community.
Conclusions
Except the above GPU-accelerated MR reconstructions, there are also a few relative applications of unclassical reconstructions which attempted to apply GPU implementation applications. For example, Johnson et al. proposed a GPU-based iterative decomposition of water and fat with echo asymmetry and least-squares (IDEAL) reconstruction scheme (61). They estimated the fat-water parameters and compared Brent’s method with golden section search to optimize the unknown MR field inhomogeneity parameter (psi) in the IDEAL equations. They claimed that their algorithm was made more robust to fat-water ambiguities using a modified planar extrapolation of psi method (61). Their experiments show that fat-water reconstruction time of their GPU-implementation methods could be quickly and robustly reduced with a factor of 11.6 on a GPU in comparison to CPU-based reconstruction.
Nowadays, GPU has been one of the standard tools in high-performance computing (2). More and more GPUs have been applied into more and more applications because of their parallel computing ability and low cost. Among the GPU-based applications of MRI reconstruction, they have been gradually recognized and widely applied. Although the early GPU programming was constrained and not friendly, the developments of GPU programming have provided more easy-to-use libraries and frameworks for programmers. GPUs have played more and more important roles in medical imaging, image reconstruction and image analysis in the clinical applications. Despite lots of successful applications have been performed in the recon community of GPU-based medical imaging, there still remains long-standing unsolved solution problems.
Firstly, GPUs’ parallel architectures require re-designing the pipeline of the reconstruction algorithms. Although there are many libraries to assist people to employ GPUs, the algorithms pre-optimized before GPU programming still can bring huge improvements than any easy-to-use libraries. It is better to consider the parallel structures in any custom-designed algorithms for GPU computing. In addition, the hybrid architectures based on GPU computing and traditional ×86 CPU-based high-performance computing clusters are more and more popular, even the cloud computing appears in industry. While software and hardware trends are not the primary problems of medical image computing, the ability that is efficiently employing more sophisticated algorithms as faster technology emerges is still an important driving force, largely precluding any kind of convergence in algorithms (47).
In the future, the computing efficiency of the custom-designed optimized algorithms, especially MRI reconstruction based on GPUs and DL, should be synthetically considered as the sequential and parallel procedure, and the low-cost Internet computation and storage services should be seriously considered.
Acknowledgements
Funding: This work was partially supported by the National Natural Science Foundation of China (No. 61471350, 81729003), the Basic Research Program of Shenzhen (JCYJ20150831154213680), and the Key Laboratory for Magnetic Resonance and Multimodality Imaging of Guangdong Province (2014B030301013).
Footnote
Conflicts of Interest: The authors have no conflicts of interest to declare.
References
- Almasi GS. Highly parallel computing. Redwood City, CA: Benjamin/Cummings, 1989.
- Shi L, Liu W, Zhang H, Xie Y, Wang D. A survey of GPU-based medical image computing techniques. Quant Imaging Med Surg 2012;2:188-206. [PubMed]
- Parallel computing. Available online: https://en.wikipedia.org/wiki/Parallel_computing. (accessed on 11 August 2016).
- Mittal S, Vetter JS. A Survey of CPU-GPU Heterogeneous Computing Techniques. ACM Computing Surveys 2015;47:69. [Crossref]
- Tarditi D, Sidd Puri S, Oglesby J. Accelerator: Using Data Parallelism to Program GPUs for General Purpose Uses. ACM SIGARCH Computer Architecture News 2006;34:325-35. [Crossref]
- Che S, Boyer M, Meng J, Tarjan D, Sheaffer JW, Skadron K. A performance study of general-purpose applications on graphics processors using CUDA. J Parallel and Distributed Computing 2008;68:1370-80. [Crossref]
- Du P, Weber R, Luszczek P, Tomov S, Peterson G, Dongarra J. From CUDA to OpenCL: Towards a Performance-portable Solution for Multi-platform GPU Programming. Parallel Computing 2012;38:391-407. [Crossref]
- Pratx G, Xing L. GPU computing in medical physics: a review. Med Phys 2011;38:2685-97. [Crossref] [PubMed]
- Boyd C. Data-Parallel Computing. ACM Queue 2008;6. [Crossref]
- Natoli V. Why 2016 Is the Most Important Year in HPC in Over Two Decades. Available online: (posted on August 23, 2016).https://www.hpcwire.com/2016/08/23/2016-important-year-hpc-two-decades/
- Future of Computing: GPGPU? Available online: (posted on July 12, 2010).http://gridtalk-project.blogspot.it/2010/07/future-of-computing-gpgpu.html
- Navarro CA, Hitschfeld-Kahler N, Mateu L. A Survey on Parallel Computing and its Applications in Data-Parallel Problems Using GPU Architectures. Commun Comput Phys 2014;15:285-329. [Crossref]
- Schenke S, Wünsche B, Denzler J. GPU-based volume segmentation. Proc. of IVCNZ 2005;05:171-6.
- Chen HL, Samavati FF, Sousa MC, Mitchell JR. Sketch-based Volumetric Seeded Region Growing. EUROGRAPHICS Workshop on Sketch-Based Interfaces and Modeling 2006:123-9.
- Beyer J, Langer C, Fritz L, Hadwiger M, Wolfsberger S, Bühler K. Interactive diffusion-based smoothing and segmentation of volumetric datasets on graphics hardware. Methods Inf Med 2007;46:270-4. [Crossref] [PubMed]
- Wang X, Wang H. Volumetric region growing based on texture mapping. Proc. SPIE Medical Imaging, Parallel Processing of Images, and Optimization Techniques (MIPPR), 2009.
- Pan L, Gu L, Xu J. Implementation of medical image segmentation in CUDA. Proc. International Conference on Information Technology and Applications in Biomedicine (ITAB), 2008:82-5.
- GPU-Accelerated Libraries. Available online: https://developer.nvidia.com/
- Sumanaweera T, Liu D. Medical image reconstruction with the FFT. GPU Gems 2, Addison Wesley, 2005:765-84.
- Schiwietz T, Chang TC, Speier P, Westermann R. MR image reconstruction using the GPU. Proc. SPIE Medical Imaging, 2006.
- Sørensen TS, Schaeffter T, Noe KO, Hansen MS. Accelerating the nonequispaced fast Fourier transform on commodity graphics hardware. IEEE Trans Med Imaging 2008;27:538-47. [Crossref] [PubMed]
- Stone SS, Haldar JP, Tsao SC, Hwu WM, Sutton BP, Liang ZP. Accelerating Advanced MRI Reconstructions on GPUs. J Parallel Distrib Comput 2008;68:1307-18. [Crossref] [PubMed]
- Yang Z, Jacob M. Efficient NUFFT algorithm for non-Cartesian MRI reconstruction. Proc. IEEE International Symposium on Biomedical Imaging (ISBI), 2009:117-20.
- Guo H, Dai J, He Y. GPU Acceleration of PROPELLER MRI Using CUDA. Proc. International Conference on Bioinformatics and Biomedical Engineering, 2009:1-4.
- Yang J, Feng C, Zhao D. A CUDA-based reverse gridding algorithm for MR reconstruction. Magn Reson Imaging 2013;31:313-23. [Crossref] [PubMed]
- Obeid NM, Atkinson IC, Thulborn KR, Hwu WM. GPU-Accelerated Gridding for Rapid Reconstruction of Non-Cartesian MRI. Proc. ISMRM, Montreal, Canada, 2011:2547.
- Gai J, Obeid N, Holtrop JL, Wu XL, Lam F, Fu M, Haldar JP, Hwu WM, Liang ZP, Sutton BP. More IMPATIENT: A Gridding-Accelerated Toeplitz-based Strategy for Non-Cartesian High-Resolution 3D MRI on GPUs. J Parallel Distrib Comput 2013;73:686-97. [Crossref] [PubMed]
- Wu XL, Gai J, Lam F, Fu M, Haldar JP, Zhuo Y, Liang ZP, Hwu W, Sutton B. Impatient MRI: Illinois massively parallel acceleration toolkit for image reconstruction with enhanced throughput in MRI. Proc. IEEE International Symposium on Biomedical Imaging (ISBI), 2011:69-72.
- Hansen MS, Atkinson D, Sorensen TS. Cartesian SENSE and k-t SENSE reconstruction using commodity graphics hardware. Magn Reson Med 2008;59:463-8. [Crossref] [PubMed]
- Sørensen TS, Atkinson D, Schaeffter T, Hansen MS. Real-time reconstruction of sensitivity encoded radial magnetic resonance imaging using a graphics processing unit. IEEE Trans Med Imaging 2009;28:1974-85. [Crossref] [PubMed]
- Sørensen TS, Prieto C, Atkinson D, Hansen MS, Schaeffter T. GPU accelerated iterative SENSE reconstruction of radial phase encoded whole-heart MRI. Proc. ISMRM, Stockholm, Sweden, 2010:2869.
- Saybasili H, Herzka DA, Barkauskas K, Seiberlich N, Griswold MA. A Generic, Multi-Node, Multi-GPU Reconstruction Framework for Online, Real-Time, Low-Latency MRI. Proc. 21st Meet Int Soc Magn Reson Med, Salt Lake City, Utah, USA; 2013:838.
- Inam O, Qureshi M, Malik SA, Omer H. GPU-Accelerated Self-Calibrating GRAPPA Operator Gridding for Rapid Reconstruction of Non-Cartesian MRI Data. Applied Magnetic Resonance 2017;48:1055-74. [Crossref]
- Li S, Chan C, Stockmann JP, Tagare H, Adluru G, Tam LK, Galiana G, Constable RT, Kozerke S, Peters DC. Algebraic reconstruction technique for parallel imaging reconstruction of undersampled radial data: application to cardiac cine. Magn Reson Med 2015;73:1643-53. [Crossref] [PubMed]
- Zhuo Y, Sutton B, Wu XL, Haldar J, Hwu WM, Liang ZP. Sparse regularization in MRI iterative reconstruction using GPUs. Proc. International Conference on Biomedical Engineering and Informatics (BMEI), 2010:578-82.
- Smith D, Gore J, Yankeelov T, Welch E. Real-Time Compressive Sensing MRI Reconstruction Using GPU Computing and Split Bregman Methods. Proc. International Journal of Biomedical Imaging 2012.864827. [PubMed]
- Nam S, Akçakaya M, Basha T, Stehning C, Manning WJ, Tarokh V, Nezafat R. Compressed sensing reconstruction for whole-heart imaging with 3D radial trajectories: a graphics processing unit implementation. Magn Reson Med 2013;69:91-102. [Crossref] [PubMed]
- Chang CH, Yu X, Ji JX. Compressed sensing MRI reconstruction from 3D multichannel data using GPUs. Magn Reson Med 2017;78:2265-74. [Crossref] [PubMed]
- Kim D, Trzasko JD, Smelyanskiy M, Haider CR, Manduca A, Dubey P. High-performance 3D compressive sensing MRI reconstruction. Conf Proc. IEEE Eng Med Biol Soc 2010;2010:3321-4.
- Sabbagh M, Uecker M, Powell A, Leeser M, Moghari M. Cardiac MRI compressed sensing image reconstruction with a graphics processing unit. Proc. International Symposium on Medical Information and Communication Technology (ISMICT), Worcester, MA, 2016.
- Xue H, Inati S, Sørensen TS, Kellman P, Hansen MS. Distributed MRI reconstruction using Gadgetron-based cloud computing. Magn Reson Med 2015;73:1015-25. [Crossref] [PubMed]
- Zhuo Y, Wu XL, Haldar JP, Hwu WM, Liang ZP, Sutton BP. Accelerating iterative field-compensated MR image reconstruction on GPUs. Proc. IEEE International Symposium on Biomedical Imaging (ISBI), 2010:820-3.
- Wang S, Su Z, Ying L, Peng X, Zhu S, Liang F, Feng D, Liang D. Accelerating magnetic resonance imaging via deep learning. Proc. IEEE International Symposium on Biomedical Imaging (ISBI), 2016:514-7.
- Hammernik K, Knoll F, Sodickson D, Pock T. Learning a variational model for compressed sensing MRI reconstruction, Proc. the International Society of Magnetic Resonance in Medicine (ISMRM), 2016.
- Lee D, Yoo J, Ye JC. Deep residual learning for compressed sensing MRI. Proc. IEEE International Symposium on Biomedical Imaging (ISBI), 2017.
- Zhu B, Liu JZ, Rosen BR, Rosen MS. Neural Network MR Image Reconstruction with AUTOMAP: Automated Transform by Manifold Approximation. Proc. the International Society of Magnetic Resonance in Medicine (ISMRM), 2017.
- Eklund A, Dufort P, Forsberg D, LaConte SM. Medical image processing on the GPU - past, present and future. Med Image Anal 2013;17:1073-94. [Crossref] [PubMed]
- Fessler J, Sutton B. Nonuniform fast Fourier transforms using min-max interpolation. IEEE Trans Signal Process 2003;51:560-74. [Crossref]
- cuFFT User Guide. Available online: http://docs.nvidia.com/cuda/cufft/index.html
- Blaimer M, Breuer F, Mueller M, Heidemann RM, Griswold MA, Jakob PM. SMASH, SENSE, PILS, GRAPPA: how to choose the optimal method. Top Magn Reson Imaging 2004;15:223-36. [Crossref] [PubMed]
- Sodickson DK, Manning WJ. Simultaneous acquisition of spatial harmonics (SMASH): fast imaging with radiofrequency coil arrays. Magn Reson Med 1997;38:591-603. [Crossref] [PubMed]
- Pruessmann KP, Weiger M, Scheidegger MB, Boesiger P. SENSE: sensitivity encoding for fast MRI. Magn Reson Med 1999;42:952-62. [Crossref] [PubMed]
- Griswold MA, Jakob PM, Heidemann RM, Nittka M, Jellus V, Wang J, Kiefer B, Haase A. Generalized autocalibrating partially parallel acquisitions (GRAPPA). Magn Reson Med 2002;47:1202-10. [Crossref] [PubMed]
- Lustig M, Donoho D, Pauly JM. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magn Reson Med 2007;58:1182-95. [Crossref] [PubMed]
- LeCun Y, Bengio Y, Hinton G. Deep learning. Nature 2015;521:436-44. [Crossref] [PubMed]
- Schmidhuber J. Deep learning in neural networks: an overview. Neural Netw 2015;61:85-117. [Crossref] [PubMed]
- Knoll F. Leveraging the potential of neural networks for image reconstruction. Proc. the International Society of Magnetic Resonance in Medicine (ISMRM), 2017.
- Després P, Jia X. A review of GPU-based medical image reconstruction. Phys Med 2017;42:76-92. [Crossref] [PubMed]
- Vedaldi A, Lenc K. MatConvNet: Convolutional Neural Networks for MATLAB. Proc. of the 23rd ACM international conference on Multimedia, 2015:689-92.
- Abadi M, Agarwal A, Barham P, Brevdo E, Chen Z, Citro C, Corrado GS, Davis A, Dean J, Devin M, Ghemawat S, Goodfellow I, Harp A, Irving G, Isard M, Jia Y, Jozefowicz R, Kaiser L, Kudlur M, Levenberg J, Mane D, Monga R, Moore S, Murray D, Olah C, Schuster M, Shlens J, Steiner B, Sutskever I, Talwar K, Tucker P, Vanhoucke V, Vasudevan V, Viegas F, Vinyals O, Warden P, Wattenberg M, Wicke M, Yu Y, Zheng X. Tensorflow: Large-scale machine learning on heterogeneous distributed systems. arXiv preprint arXiv:1603.04467, 2016.
- Johnson DH, Narayan S, Flask CA, Wilson DL. Improved fat-water reconstruction algorithm with graphics hardware acceleration. J Magn Reson Imaging 2010;31:457-65. [Crossref] [PubMed]


